当前位置:网站首页>2 - 3 arbre de recherche
2 - 3 arbre de recherche
2022-07-07 08:26:00 【Perkinl】
2-3 Arbre de recherche(2-3-Search-Tree)
- 2-Noeud:Les noeuds d'un arbre binaire standard sont appelés2-Noeud(Contient une clé et deux liens).
- 3-Noeud:Contient deux clés et trois liens.
Définition:Un2-3Trouver un arbre ou un arbre vide,Ou comprenant les noeuds suivants:
2-Noeud,Contient une clé(Et sa valeur correspondante)Et deux liens,Le lien de gauche indique2-3Toutes les clés de l'arbre sont plus petites que ce noeud,Le lien de droite indique2-3Les clés de l'arbre sont plus grandes que ce noeud.
3-Noeud,Contient deux clés(Et sa valeur correspondante)Et trois liens,Le lien de gauche indique2-3Toutes les clés de l'arbre sont plus petites que ce noeud,Lien vers2-3Les clés de l'arbre sont toutes situées à ce noeud Entre deux touches,Le lien de droite indique2-3Les clés de l'arbre sont plus grandes que ce noeud.
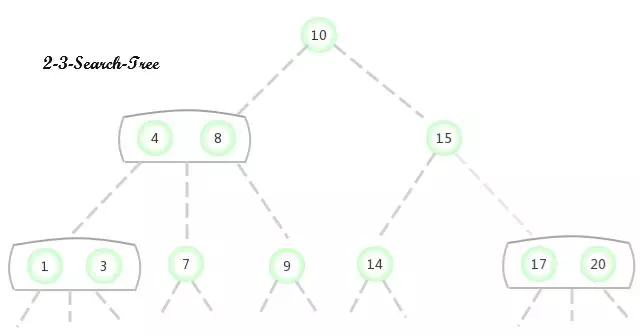
2-3 Arbre de recherche(2-3-Search-Tree) Fonctionnement
Un équilibre parfait2-3La distance entre tous les liens vides dans l'arbre de recherche et le noeud racine doit être la même.
Trouver
2-3 La recherche dans l'arbre de recherche est similaire à la recherche dans l'arbre de recherche binaire.Pour déterminer si une clé est dans l'arbre,Comparez - le d'abord à la clé dans le noeud racine.Si ça et l'un d'eux Équivalence,Trouver les Hits.Sinon,Trouver un lien vers l'intervalle correspondant à partir des résultats de la comparaison, Et continuer à chercher Récursivement dans le Sous - arbre qu'il pointe . Si c'est un lien vide ,Trouver des ratés.
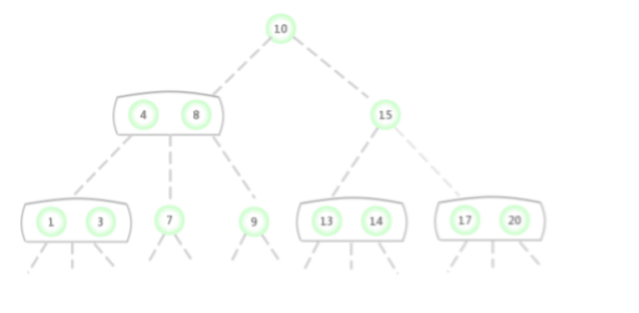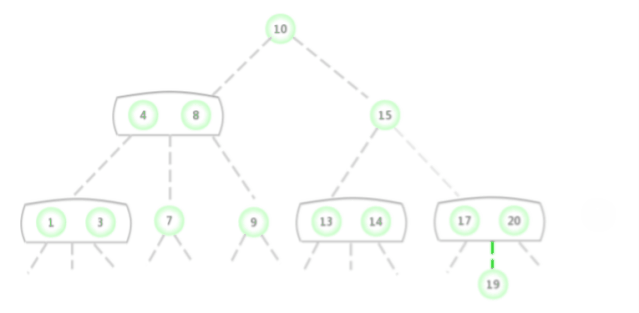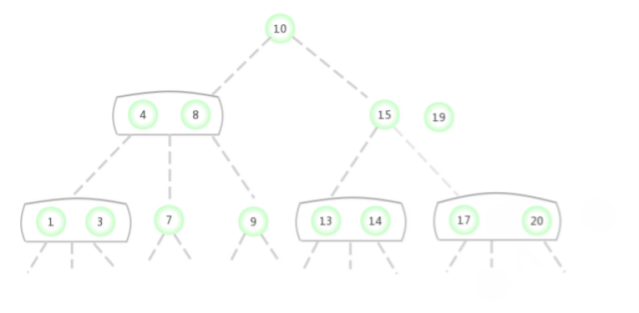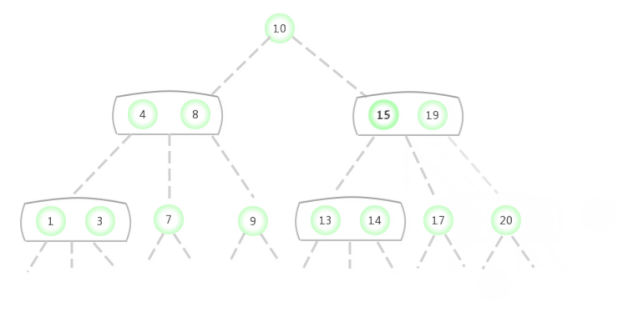
Dans la figure ci - dessus2-3 La clé de recherche dans l'arbre est 2Si le noeud existe,La procédure est la suivante:
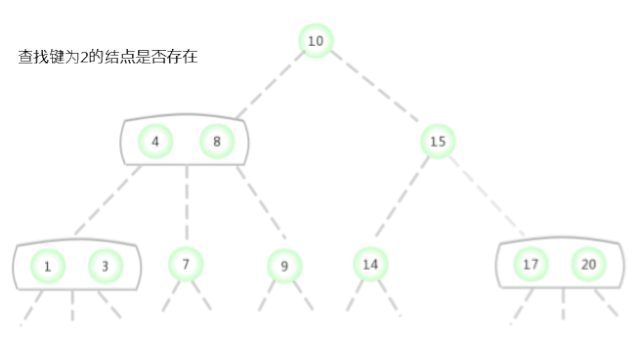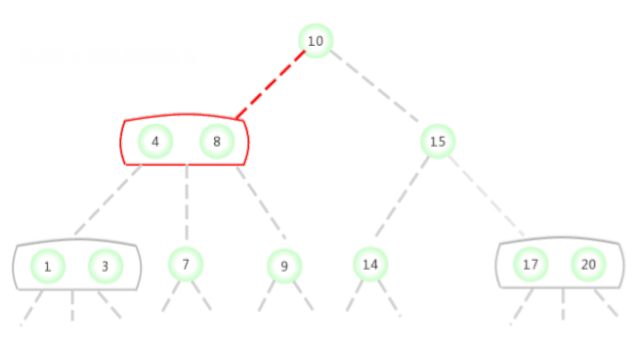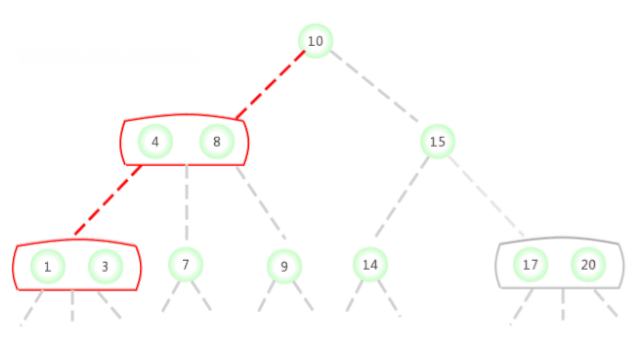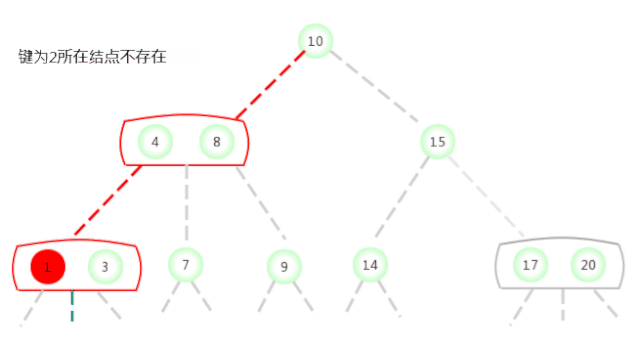
Dans la figure ci - dessus2-3 La clé de recherche dans l'arbre est 17Si le noeud existe,La procédure est la suivante:
Insérer
Vers2-Insérer une nouvelle clé dans le noeud
Oui.2-3 Insérer un nouveau noeud dans l'arbre , Insertion similaire à l'arbre de recherche binaire , Une recherche manquée en première ligne , Trouver l'emplacement du noeud à insérer , Accrochez - le au bas de l'arbre . Mais de cette façon, l'arbre ne peut pas garantir un équilibre parfait .Utiliser2-3Principales causes: Capable de maintenir l'équilibre après l'insertion d'un nouveau noeud .
Si la recherche manquée se termine par un 2-Noeud,Prends ça.2-NoeudRemplacer par:3-Noeud, Enregistrer la clé à insérer dans .
Si la recherche manquée se termine par un 3-Noeud,Le processus d'analyse est le suivant.
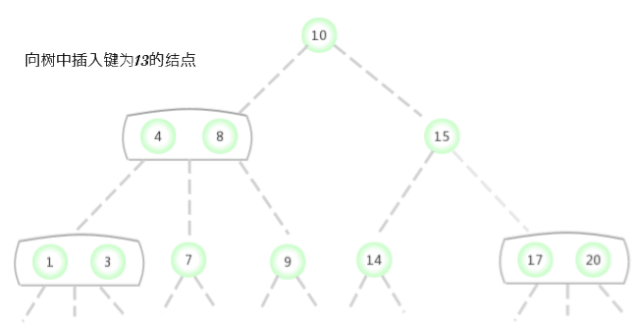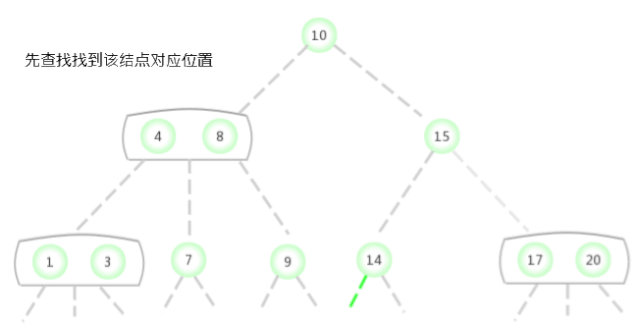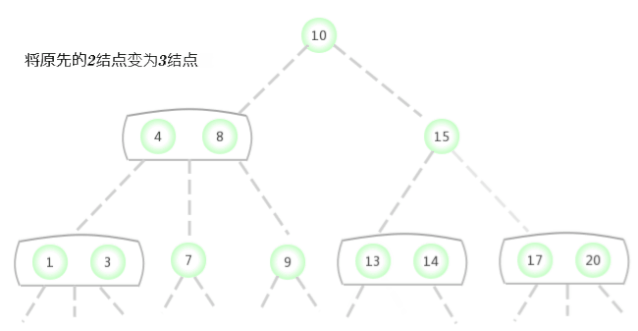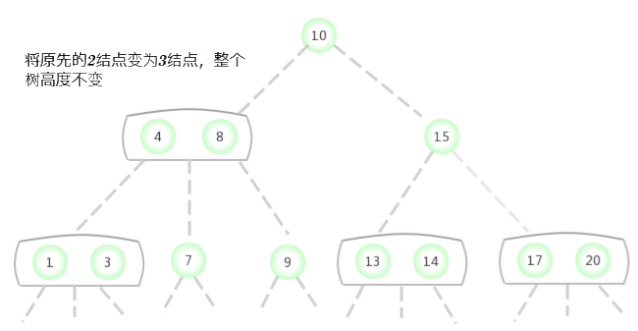
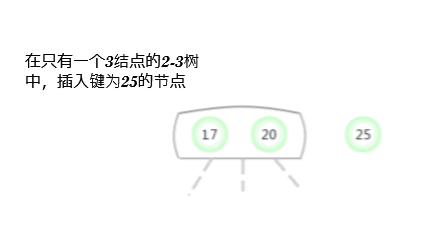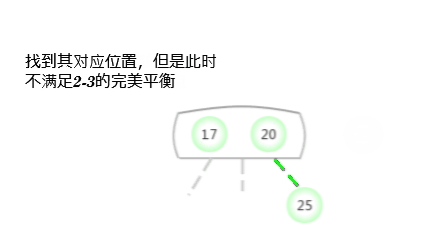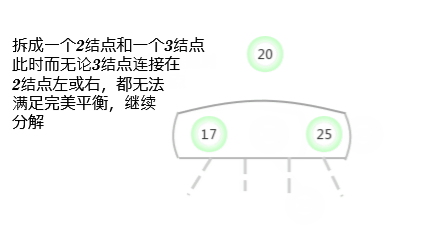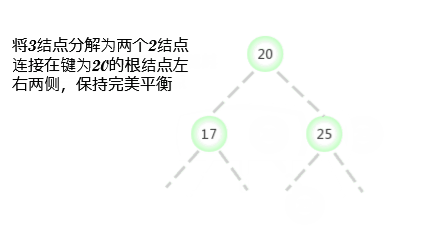
Un arbre ne contient qu'un seul3-Insérer une nouvelle clé dans l'arbre du noeud
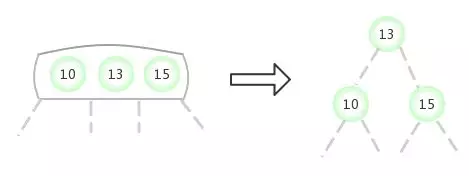
Avant d'examiner la situation générale , Supposons d'abord qu'on ait besoin d'un arbre qui ne contient qu'un seul 3- Insérer une nouvelle clé dans l'arbre du noeud . Il y a deux clés dans cet arbre , Donc dans son seul noeud Il n'y a plus de place pour insérer une nouvelle clé . Pour insérer une nouvelle clé , D'abord, sauvegardez temporairement la nouvelle clé dans ce noeud ,Pour former un4-Noeud(Contient:3Les clés et4Les liens).Créer un4-NoeudC'est pratique., Parce qu'il est facile de le transformer en un arbre 3- Oui.2-NoeudComposition2-3Arbre, Un des noeuds (Racine) Contient la clé moyenne , Un noeud contient 3 La plus petite des clés ( Connecté au lien gauche du noeud racine ), Un noeud contient 3 La plus grande des clés ( Connecté au lien droit du noeud racine ). Cet arbre est un arbre qui contient 3 Arbre de recherche binaire de noeuds , C'est aussi un équilibre parfait 2-3Arbre, Parce que tout ça La distance entre le lien vide et le noeud est égale . La hauteur de l'arbre avant l'insertion est 0, La hauteur de l'arbre après insertion est 1.
Un noeud parent est2-Nodulaire3-Insérer une nouvelle clé dans le noeud
Supposons que la recherche manquée se termine par un 3-Noeud, Et son noeud parent est un 2-Noeud.Dans ce cas: Pour les nouvelles clés tout en maintenant l'équilibre parfait de l'arbre Faire de la place. Il faut construire un 4-Noeud Et la décomposer , Mais un nouveau noeud n'est pas créé pour la clé du milieu , Au lieu de cela, déplacez - le dans le noeud parent original .
Considérez cette transition comme une direction vers l'original 3-Noeud Remplacer un lien par deux liens à gauche et à droite de la clé centrale originale dans le nouveau noeud parent , Et pointer vers deux nouveaux 2-Noeud. D'après les hypothèses, De l'espace pétrolier dans le noeud parent : Le noeud parent est un 2-Noeud, Après l'insertion, il devient un 3-Noeud.En plus, Cette conversion n'affecte pas non plus (Parfaitement équilibré)2-3ArbreDe Nature principale . Les arbres sont toujours en ordre , Parce que la clé du milieu a été déplacée dans le noeud parent ; Les arbres sont toujours parfaitement équilibrés , La distance entre tous les noeuds foliaires et les noeuds racinaires reste la même après l'insertion .
Le processus décrit ci - dessus est2-3 Le coeur de la dynamique des arbres , L'illustration montre ce qui suit :
Un noeud parent est3-Nodulaire3-Insérer une nouvelle clé dans le noeud
Supposons que la recherche d'erreurs se termine par un noeud parent avec 3-NoeudDe3-Noeud. Il faut encore construire un 4-Noeud Et la décomposer , Puis insérez sa clé centrale dans son noeud parent . Parce que le noeud parent est aussi un 3-Noeud, Insérer au milieu pour former un nouveau temporaire 4-Noeud, Ensuite, faites la même transformation sur ce noeud , Set décompose ce noeud parent et insère sa clé centrale dans son noeud parent . Extension à la situation générale , C'est comme ça qu'on a continué à décomposer l'improviste 4-Noeud Et insérez la clé du milieu dans le noeud parent supérieur ,Jusqu'à ce que vous rencontriez un2-Noeud Et le remplacer par un 3-Noeud, Ou arriver 3-NoeudRacine de.
Le processus illustré est le suivant:
Démonter le noeud racine
Si tout est sur le chemin du noeud d'insertion au noeud racine 3-Noeud, Le noeud racinaire finit par devenir un 4-Noeud. Il n'y a qu'un seul arbre *3-Noeud Comment insérer une nouvelle clé dans l'arbre pour résoudre ce problème .Sera temporaire4-Noeud Divisé en trois 2-Noeud**,Tree gauga1. Ce dernier changement maintient l'équilibre parfait de l'arbre , Parce qu'il transforme le noeud racine .
Le processus illustré est le suivant:
4- Décomposition des noeuds
In2-3ArbreMoyenne4-Noeud Il y a plusieurs situations où .
- 1.Noeud racinaire
- 2.Le noeud parent est2-Noeud Sous - noeud gauche ou sous - noeud droit de
- 3.Le noeud parent est3-NoeudEnfant gauche de、 Sous - noeud intermédiaire ou sous - noeud droit
Maintenant, regardons plus en détail 2-3Arbre Comment se décomposer lorsque l'emplacement ci - dessus apparaît dans .
Situation:
Quand temporaire 4-Noeud Apparaît au noeud racine :
Quand temporaire 4-NoeudApparaît dans2-NoeudDu côté gauche:
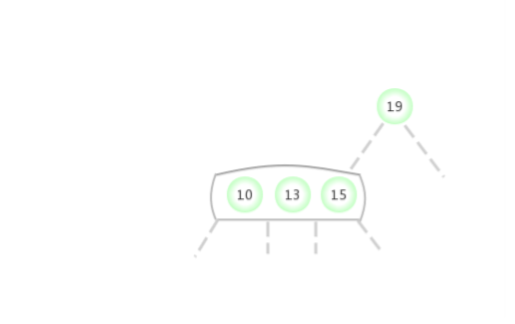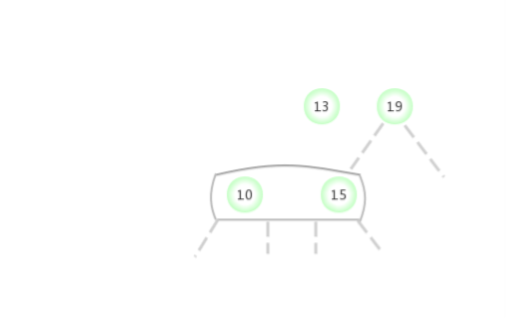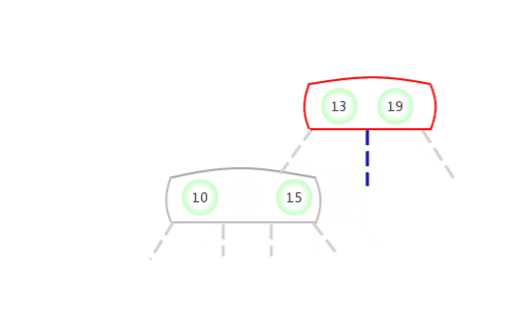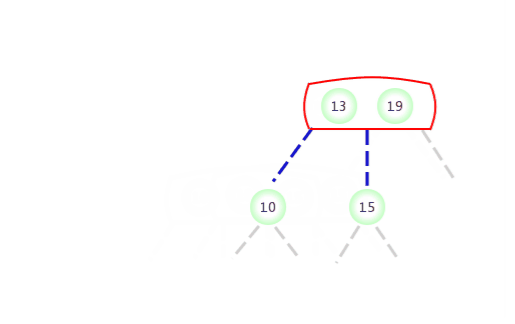
Quand temporaire 4-NoeudApparaît dans2-NoeudÀ droite de:
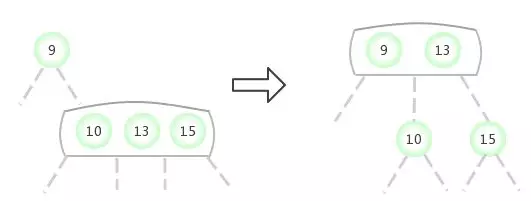
Quand temporaire 4-NoeudApparaît dans3-NoeudDu côté gauche:
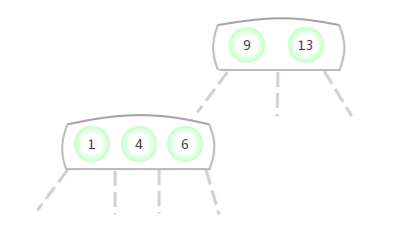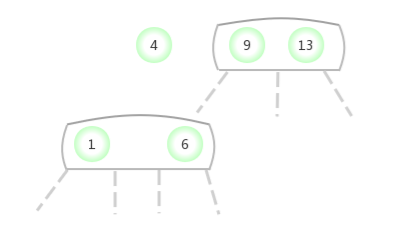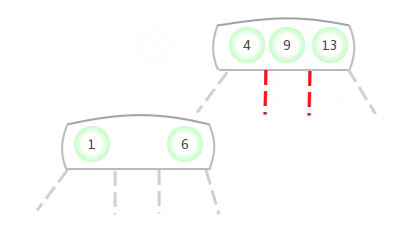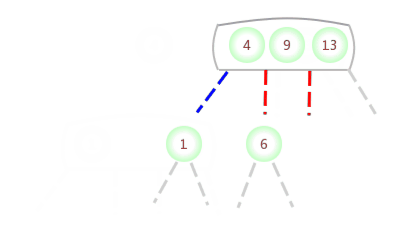
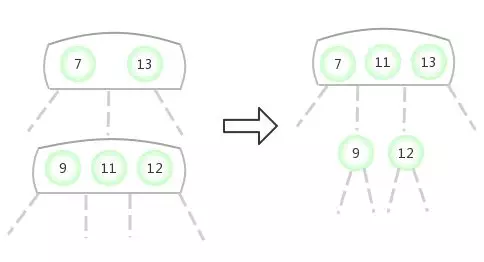
Quand temporaire 4-NoeudApparaît dans3-NoeudAu milieu de:
Quand temporaire 4-NoeudApparaît dans3-NoeudÀ droite de:
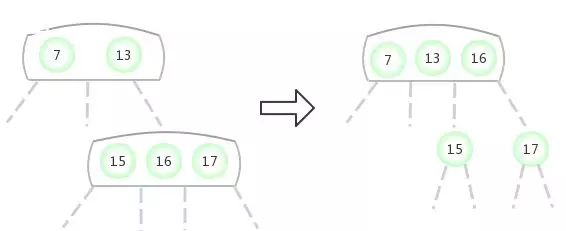
Dans ce cas , Dans le processus de changement , Seulement si le noeud racine est finalement temporaire 4-Noeud, À ce moment - là, il est décomposé en 3- Oui.2-NoeudHeure, La hauteur de l'arbre augmente 1.En plus de ça,,Insérer un noeud2-3 La hauteur de l'arbre est toujours la même . Dans le processus de changement décrit ci - dessus : Toute longueur de chemin vide liée au noeud racine est égale .
Conclusions
Dans un arbre de NDe2-3Dans l'arbre, Les opérations de recherche et d'insertion n'accèdent pas nécessairement aux noeuds plus que lgN.
- Preuve:Un arbre contenantNLes noeuds2-3 La hauteur de l'arbre est log2 NEtlog3 NEntre.
边栏推荐
- The simple problem of leetcode is to judge whether the number count of a number is equal to the value of the number
- Qinglong panel -- finishing usable scripts
- [quick start of Digital IC Verification] 11. Introduction to Verilog testbench (VTB)
- The largest 3 same digits in the string of leetcode simple question
- 云原生存储解决方案Rook-Ceph与Rainbond结合的实践
- CTF-WEB shrine模板注入nmap的基本使用
- Openvscode cloud ide joins rainbow integrated development system
- One click deployment of highly available emqx clusters in rainbow
- GFS分布式文件系统
- Opencv learning notes 1 -- several methods of reading images
猜你喜欢
Deit learning notes
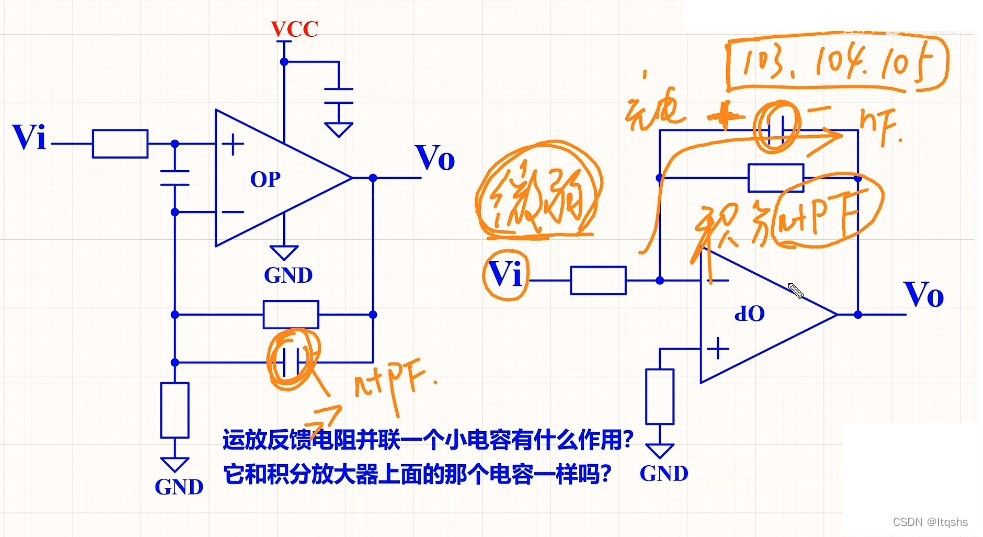
What is the function of paralleling a capacitor on the feedback resistance of the operational amplifier circuit
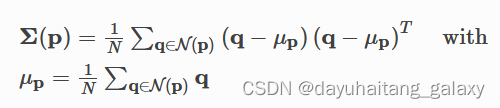
Open3d ISS key points
Use of JMeter
Rainbow version 5.6 was released, adding a variety of installation methods and optimizing the topology operation experience

解析机器人科技发展观对社会研究论
藏书馆App基于Rainbond实现云原生DevOps的实践

Splunk子查询模糊匹配csv中字段值为*
Tuowei information uses the cloud native landing practice of rainbow

Basic use of CTF web shrink template injection nmap
随机推荐
Transformation function map and flatmap in kotlin
Automatic upgrading of database structure in rainbow
Obsidan之数学公式的输入
柯基数据通过Rainbond完成云原生改造,实现离线持续交付客户
Opencv learning note 4 - expansion / corrosion / open operation / close operation
OpenVSCode云端IDE加入Rainbond一体化开发体系
Openvscode cloud ide joins rainbow integrated development system
MES system is a necessary choice for enterprise production
Explore creativity in steam art design
Snyk 依赖性安全漏洞扫描工具
Pvtv2--pyramid vision transformer V2 learning notes
Practice of combining rook CEPH and rainbow, a cloud native storage solution
Register of assembly language by Wang Shuang
The reified keyword in kotlin is used for generics
利用 Helm 在各类 Kubernetes 中安装 Rainbond
DeiT学习笔记
Standard function let and generic extension function in kotlin
Fluentd is easy to use. Combined with the rainbow plug-in market, log collection is faster
在Rainbond中实现数据库结构自动化升级
【无标题】