当前位置:网站首页>Obsidan之数学公式的输入
Obsidan之数学公式的输入
2022-07-07 05:23:00 【流岁金沙】
前言:
最近在学习专升本的高数,还想继续使用Obsidian作为笔记软件,但是苦于不知道数学公式怎么输入,于是有了这一篇文章
LaTex的语法
注意:这里的数学公式都要在$在这$,或者$$在这$$
先说下怎么换行
$$
\begin{aligned}a=b+c\\b=c-a\\c=a+b \end{aligned}
$$
a = b + c b = c − a c = a + b \begin{aligned}a=b+c\\b=c-a\\c=a+b \end{aligned} a=b+cb=c−ac=a+b
$$
\begin{matrix}已知y=\sqrt{x+3}&&(x>=0)\\求y的最大值是多少 \end{matrix}
$$
已 知 y = x + 3 ( x > = 0 ) 求 y 的 最 大 值 是 多 少 \begin{matrix}已知y=\sqrt{x+3}&&(x>=0)\\求y的最大值是多少 \end{matrix} 已知y=x+3求y的最大值是多少(x>=0)
$$
\begin{bmatrix}已知y=\sqrt{x+3}&&(x>=0)\\求y的最大值是多少 \end{bmatrix}
$$
[ 已 知 y = x + 3 ( x > = 0 ) 求 y 的 最 大 值 是 多 少 ] \begin{bmatrix}已知y=\sqrt{x+3}&&(x>=0)\\求y的最大值是多少 \end{bmatrix} [已知y=x+3求y的最大值是多少(x>=0)]
$$
\begin{Bmatrix}已知y=\sqrt{x+3}&&(x>=0)\\求y的最大值是多少 \end{Bmatrix}
$$
{ 已 知 y = x + 3 ( x > = 0 ) 求 y 的 最 大 值 是 多 少 } \begin{Bmatrix}已知y=\sqrt{x+3}&&(x>=0)\\求y的最大值是多少 \end{Bmatrix} { 已知y=x+3求y的最大值是多少(x>=0)}
$$
\begin{vmatrix}
0&1&2\\
3&4&5\\
6&7&8\\
\end{vmatrix}
$$
∣ 0 1 2 3 4 5 6 7 8 ∣ \begin{vmatrix} 0&1&2\\ 3&4&5\\ 6&7&8\\ \end{vmatrix} ∣∣∣∣∣∣036147258∣∣∣∣∣∣
$$
\begin{Vmatrix}
0&1&2\\
3&4&5\\
6&7&8\\
\end{Vmatrix}
$$
∥ 0 1 2 3 4 5 6 7 8 ∥ \begin{Vmatrix} 0&1&2\\ 3&4&5\\ 6&7&8\\ \end{Vmatrix} ∥∥∥∥∥∥036147258∥∥∥∥∥∥
- 希腊字母
α \alpha α、 β \beta β、 χ \chi χ、 Δ \Delta Δ、 Γ \Gamma Γ、 Θ \Theta Θ之类的

- 一些数学结构

- 效果如下:
$\frac{123}{999}$、$\sqrt[n]{abc}$、$\frac{\sqrt{234}}{\sqrt[n]{abc}}$、$\underrightarrow{abc}$、$\overrightarrow{abc}$
123 999 \frac{123}{999} 999123、 a b c n \sqrt[n]{abc} nabc、 234 a b c n \frac{\sqrt{234}}{\sqrt[n]{abc}} nabc234、 a b c → \underrightarrow{abc} abc、 a b c → \overrightarrow{abc} abc
- 插入定界符

- 效果如下
$|$、$\|$、$\Uparrow$、$\{\}$
∣ | ∣、 ∥ \| ∥、 ⇑ \Uparrow ⇑、 { } \{\} { }
- 插入一些可变大小的符号

效果如下:
$\sum$、$\int$、$\oint$、$\iint$、$\bigcap\bigcup\bigoplus\bigotimes$
∑ \sum ∑、 ∫ \int ∫、 ∮ \oint ∮、 ∬ \iint ∬、 ⋂ ⋃ ⨁ ⨂ \bigcap\bigcup\bigoplus\bigotimes ⋂⋃⨁⨂
- 插入一些函数名称

效果如下:
$\sin$、$\cos$、$\tan$、$\log$、 $\tan(at-n\pi)$
sin \sin sin、 cos \cos cos、 tan \tan tan、 log \log log、 tan ( a t − n π ) \tan(at-n\pi) tan(at−nπ)
- 关系运算符和二进制运算符

效果如下:
$\times$、$\ast$、$\div$、$\pm$、$\leq$、$\geq$、$\neq$、$\thickapprox$、$\sqsupset$、$\subset$、$\supseteq$、$\sqsupset$、$\sqsupseteq$、$\in$
× \times ×、 ∗ \ast ∗、 ÷ \div ÷、 ± \pm ±、 ≤ \leq ≤、 ≥ \geq ≥、 ≠ \neq =、 ≈ \thickapprox ≈、 ⊐ \sqsupset ⊐、 ⊂ \subset ⊂、 ⊇ \supseteq ⊇、 ⊐ \sqsupset ⊐、 ⊒ \sqsupseteq ⊒、 ∈ \in ∈
- 插入箭头符号

效果如下:
$\leftarrow$、$\Leftarrow$、$\nLeftarrow$、$\rightleftarrows$
← \leftarrow ←、 ⇐ \Leftarrow ⇐、 ⇍ \nLeftarrow ⇍、 ⇄ \rightleftarrows ⇄
- 其他符号
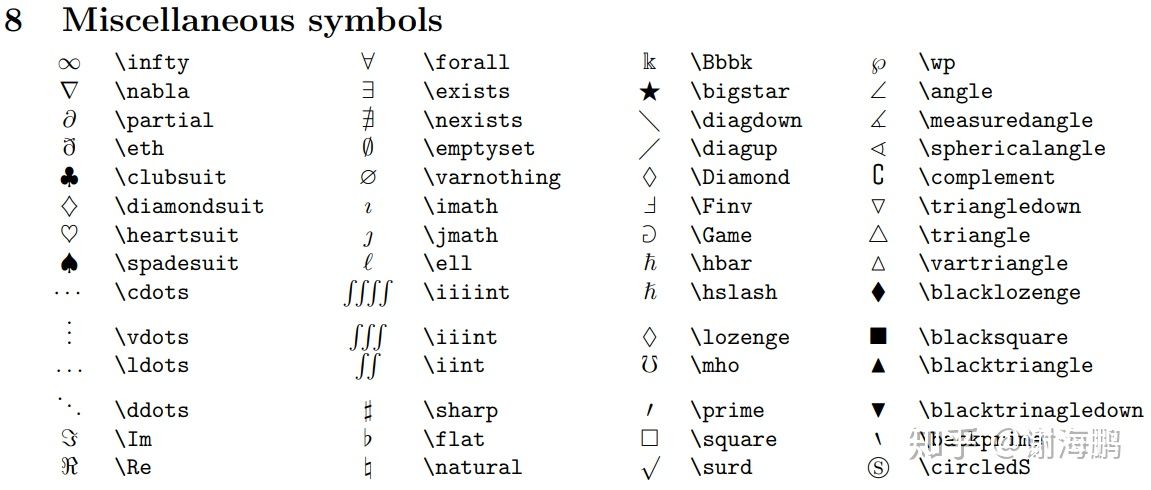
- 效果如下
$\infty$、$\angle$、$\int$、$\triangle$、$\square$
∞ \infty ∞、 ∠ \angle ∠、 ∫ \int ∫、 △ \triangle △、 □ \square □
- 插入上下标
用^表示上标,用_表示下标记
效果如下:
sin 2 ( θ ) + cos 2 ( θ ) = 1 \sin^2(\theta) + \cos^2(\theta) = 1 sin2(θ)+cos2(θ)=1
∑ n = 1 ∞ k \sum_{n=1}^\infty k n=1∑∞k
∫ a b f ( x ) d x \int_a^bf(x)\,dx ∫abf(x)dx
lim x → ∞ exp ( − x ) = 0 \lim\limits_{x\to\infty}\exp(-x) = 0 x→∞limexp(−x)=0
注意:
\,在积分里的作用是为了增加些许间距,\!会减少一些间距。输出分段函数
用\begin{cases}和\end{cases}来构造分段函数,中间则用\\来分段
f ( x ) = { 2 x , x > 0 3 x , x ≤ 0 f(x) = \begin{cases} 2x,\,\,x>0\\ 3x,\,\,x\le0\\ \end{cases} f(x)={ 2x,x>03x,x≤0
- 一些常见的数学公式
$$
f'(x) = x^2 + x
$$
f ′ ( x ) = x 2 + x f'(x) = x^2 + x f′(x)=x2+x
$$
\lim_{x\to0}\frac{9x^5+7x^3}{x^2+6x^8}
$$
lim x → 0 9 x 5 + 7 x 3 x 2 + 6 x 8 \lim_{x\to0}\frac{9x^5+7x^3}{x^2+6x^8} x→0limx2+6x89x5+7x3
$$
\int_a^b f(x)\,dx
$$
∫ a b f ( x ) d x \int_a^b f(x)\,dx ∫abf(x)dx
$$
\int_0^{+\infty}f(x)\,dx
$$
∫ 0 + ∞ f ( x ) d x \int_0^{+\infty}f(x)\,dx ∫0+∞f(x)dx
$$
\int_{x^2+y^2\leq R^2} \,f(x,y)\,dx\,dy = \int_{\theta=0}^{2\pi}\int_{r=0}^R \,f(r\cos\theta,r\sin\theta)\,r\,dr\,d\theta
$$
∫ x 2 + y 2 ≤ R 2 f ( x , y ) d x d y = ∫ θ = 0 2 π ∫ r = 0 R f ( r cos θ , r sin θ ) r d r d θ \int_{x^2+y^2\leq R^2} \,f(x,y)\,dx\,dy = \int_{\theta=0}^{2\pi}\int_{r=0}^R \,f(r\cos\theta,r\sin\theta)\,r\,dr\,d\theta ∫x2+y2≤R2f(x,y)dxdy=∫θ=02π∫r=0Rf(rcosθ,rsinθ)rdrdθ
$$
\int\!\!\!\int_D f(x,y)dxdy
$$
∫ ∫ D f ( x , y ) d x d y \int\!\!\!\int_D f(x,y)dxdy ∫∫Df(x,y)dxdy
参考:
https://zhuanlan.zhihu.com/p/158156773
边栏推荐
- One click installation of highly available Nacos clusters in rainbow
- Leetcode simple question: find the K beauty value of a number
- Don't stop chasing the wind and the moon. Spring mountain is at the end of Pingwu
- Open3D ISS关键点
- Rainbow version 5.6 was released, adding a variety of installation methods and optimizing the topology operation experience
- Full text query classification
- eBPF Cilium实战(2) - 底层网络可观测性
- 云原生存储解决方案Rook-Ceph与Rainbond结合的实践
- buureservewp(2)
- [IELTS speaking] Anna's oral learning records Part3
猜你喜欢
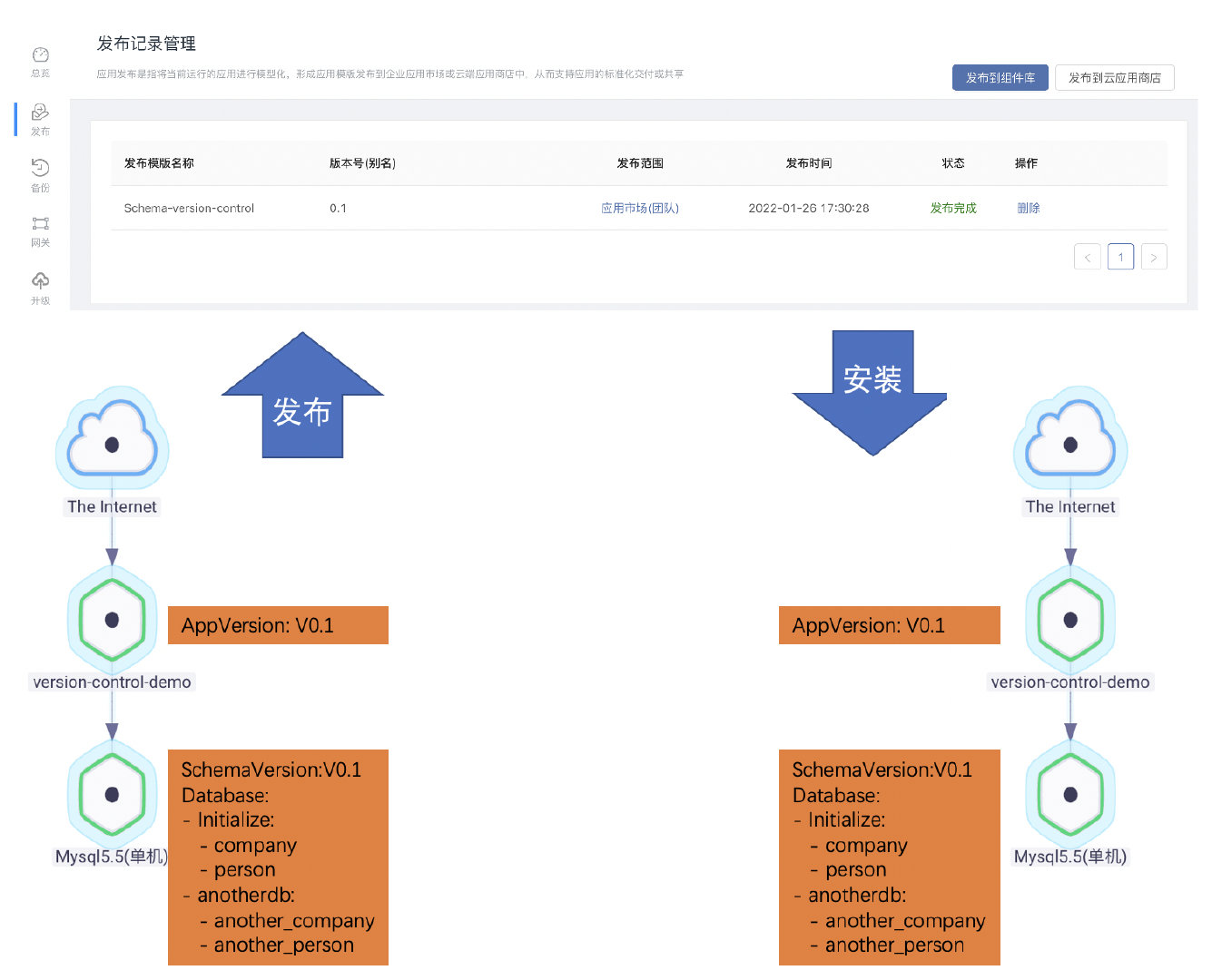
在Rainbond中实现数据库结构自动化升级
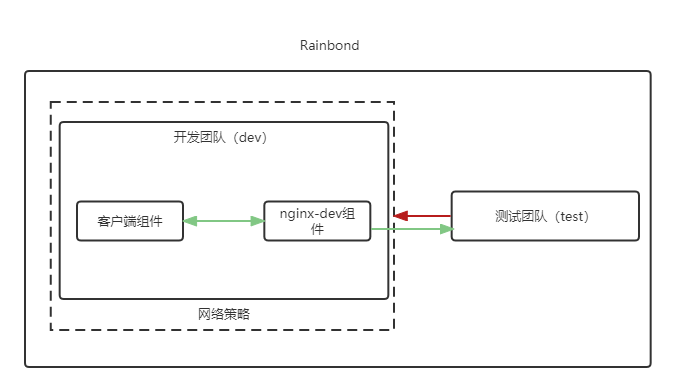
eBPF Cilium实战(1) - 基于团队的网络隔离
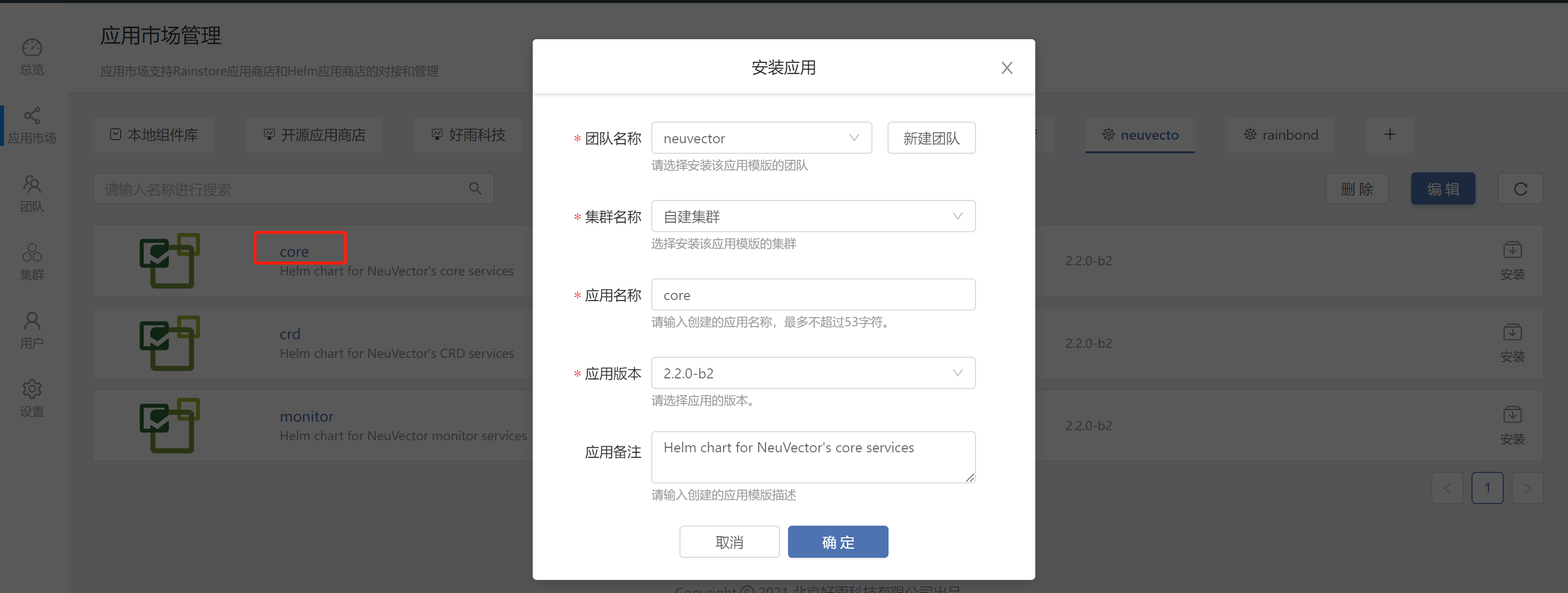
Rainbow combines neuvector to practice container safety management

The truth of robot education in hands-on practice
Splunk中single value视图使用将数值替换为文字
单场带货涨粉10万,农村主播竟将男装卖爆单?

opencv学习笔记三——图像平滑/去噪处理

PVTV2--Pyramid Vision TransformerV2学习笔记
Ebpf cilium practice (2) - underlying network observability

使用 Nocalhost 开发 Rainbond 上的微服务应用
随机推荐
BiSeNet的特點
OpenVSCode云端IDE加入Rainbond一体化开发体系
Detailed explanation of apply, also, let, run functions and principle analysis of internal source code in kotlin
Interpreting the practical application of maker thinking and mathematics curriculum
The use of generics and vararg variable parameters in kotlin
JS copy picture to clipboard read clipboard
Avatary's livedriver trial experience
Excel import function of jeesite form page
IP-guard助力能源企业完善终端防泄密措施,保护机密资料安全
积分商城管理系统中应包含的四大项
CCTV is so warm-hearted that it teaches you to write HR's favorite resume hand in hand
Openjudge noi 2.1 1752: chicken and rabbit in the same cage
The simple problem of leetcode is to judge whether the number count of a number is equal to the value of the number
饥荒云服管理脚本
Fast parsing intranet penetration escorts the document encryption industry
Blob object introduction
offer收割机:两个长字符串数字相加求和(经典面试算法题)
探索STEAM艺术设计中的创造力
Zcmu--1396: queue problem (2)
【雅思口语】安娜口语学习记录 Part3