当前位置:网站首页>复杂网络建模(二)
复杂网络建模(二)
2022-07-07 04:58:00 【坝坝头伯爵】
介数
介数分为节点介数和边介数,反映了节点或边在整个网络中的作用和影响力。
节点的介数Bi定义为
B i = ∑ j ≠ l ≠ i [ N j l ( i ) / N j l ] B_i=\sum_{j\neq l\neq i}^{}[N_{jl}(i)/N_jl] Bi=j=l=i∑[Njl(i)/Njl]
其中,Njl表示节点Vj和节点Vl之间的最短路径条数,Njl(i)表示节点Vj和节点Vl之间的最短路径经过节点Vi的条数。
边的介数Bij定义为
B i j = ∑ ( l , m ) ≠ ( i , j ) [ N l m ( e i j ) / N l m ] B_{ij}=\sum_{ {(l,m)}\neq (i,j)}^{}[N_{lm}(e_{ij})/N_lm] Bij=(l,m)=(i,j)∑[Nlm(eij)/Nlm]
式中,Nlm表示节点Vl和Vm之间的最短路径条数,Nlm(eij)表示节点Vl和Vm之间的最短路径经过边eij的条数。
核度
一个图的k-核是指反复去掉度值小于k的节点及其连线后,所剩的子图,该子图的节点数就是该核的大小。
节点核度的最大值叫做网络的核度。
网络密度
网络密度指的是一个网络中个节点之间联络的紧密程度。网络G的网络密度d(G)定义为
d ( G ) = 2 M / [ N ( N − 1 ) ] d(G)=2M/[N(N-1)] d(G)=2M/[N(N−1)]
M为网络中实际拥有的连接数,N为网络节点数,当网络完全连通时,密度为1.
边栏推荐
- Leanote private cloud note building
- Linux server development, MySQL stored procedures, functions and triggers
- Pytest + allure + Jenkins Environment - - achèvement du remplissage de la fosse
- Force buckle 145 Binary Tree Postorder Traversal
- The zblog plug-in supports the plug-in pushed by Baidu Sogou 360
- Implementation of replacement function of shell script
- Codeforces Global Round 19
- [Matlab] Simulink 自定义函数中的矩阵乘法工作不正常时可以使用模块库中的矩阵乘法模块代替
- Find the mode in the binary search tree (use medium order traversal as an ordered array)
- 海信电视开启开发者模式
猜你喜欢

让Livelink初始Pose与动捕演员一致
buureservewp(2)
Thinkcmf6.0 installation tutorial

央视太暖心了,手把手教你写HR最喜欢的简历
Linux server development, MySQL index principle and optimization
Explore Cassandra's decentralized distributed architecture
Padavan manually installs PHP
Force buckle 144 Preorder traversal of binary tree

Codeforces Global Round 19
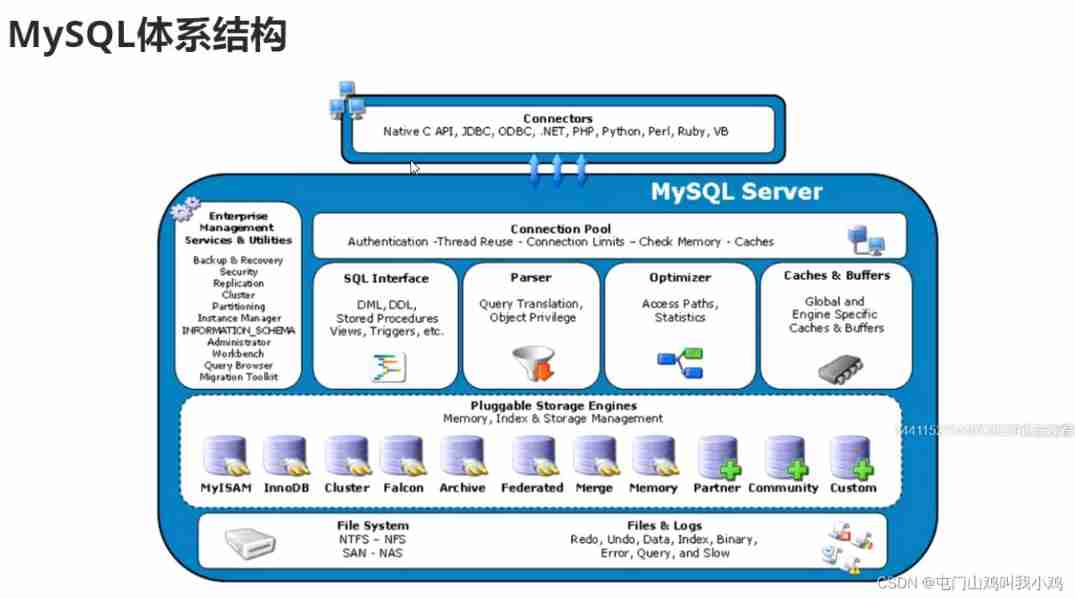
Linux server development, SQL statements, indexes, views, stored procedures, triggers
随机推荐
buureservewp(2)
2022 Inner Mongolia latest advanced fire facility operator simulation examination question bank and answers
Network learning (III) -- highly concurrent socket programming (epoll)
C语言航班订票系统
DNS server configuration
mysql多列索引(组合索引)特点和使用场景
Binary tree and heap building in C language
探索干货篇!Apifox 建设思路
Linux server development, MySQL stored procedures, functions and triggers
Quickly use Jacobo code coverage statistics
Pytest+allure+jenkins installation problem: pytest: error: unrecognized arguments: --alluredir
Lattice coloring - matrix fast power optimized shape pressure DP
[CV] Wu Enda machine learning course notes | Chapter 8
[UVM foundation] what is transaction
互动送书-《Oracle DBA工作笔记》签名版
json 数据展平pd.json_normalize
Content of string
OpenJudge NOI 2.1 1752:鸡兔同笼
QT learning 26 integrated example of layout management
Thinkcmf6.0安装教程