当前位置：网站首页>强化学习-学习笔记1 | 基础概念

强化学习-学习笔记1 | 基础概念

2022-07-04 12:33:00 【climerecho】

1. 基本概念

1.1 概率论的基础知识

a. 随机变量

概念：是一个未知的量，值是由随机事件结果来决定的。

使用大写 X 来表示随机变量
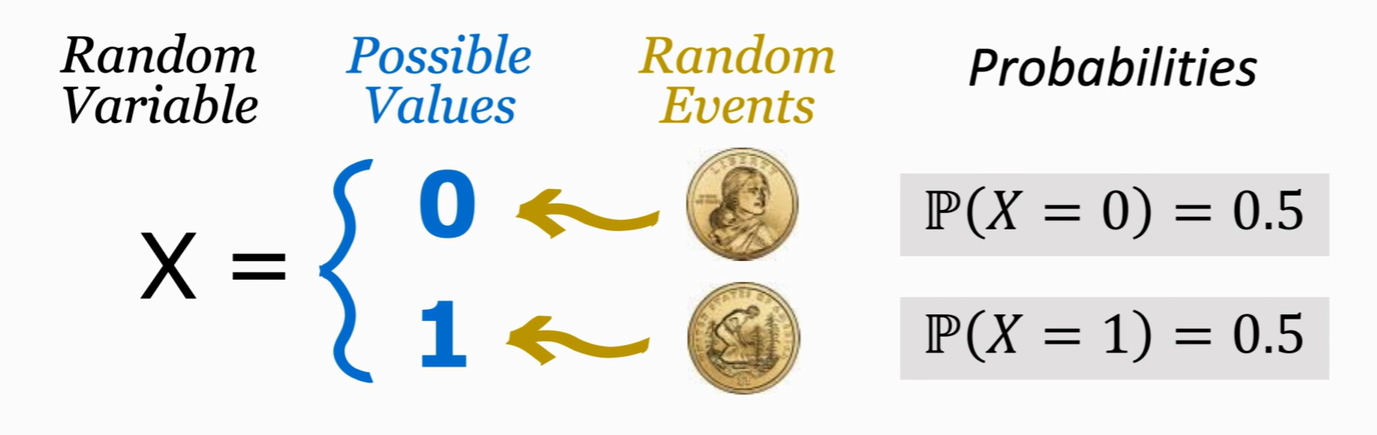
如在抛硬币之前我是不知道硬币结果是什么，但是我知道事件的概率
使用小写 x 来表示随机变量 X 的观测值，只是表示一个数，没有随机性，如下面观测到三次抛硬币的结果
观测值：当随机事件结束，会表征出一个结果，比如硬币落地后是正 / 反面朝上
- x₁ = 0
- x₂ = 1
- x₃ = 1

b. 概率密度函数

Probability Density Function，PDF.

意义：随机变量再某个确定的取值点附近的可能性。

举例理解：

连续分布：

如高斯分布这个连续分布

\[p(x)=\frac{1}{\sqrt{2\pi\sigma^2}}exp({-\frac{x-\mu}{2\sigma^2}}) \]

μ 为均值，σ 为标准差。

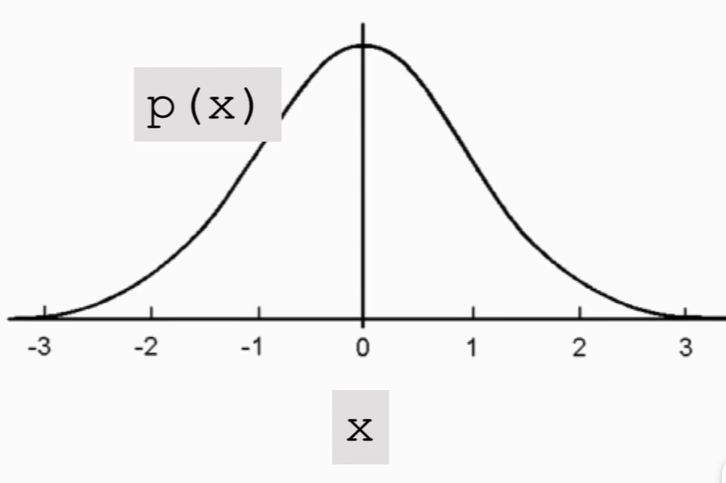
横轴是随机变量 X 取值，纵轴是概率密度，曲线是高斯分布概率密度函数P(X)，说明在原点附近概率取值比较大，在远离原点附近概率取值比较小

离散分布：

对于离散随机变量：X∈1,3,7

则对应的 PDF 为:

\[p(1)=0.2, p(3) = 0.5, p(7)=0.3 \]

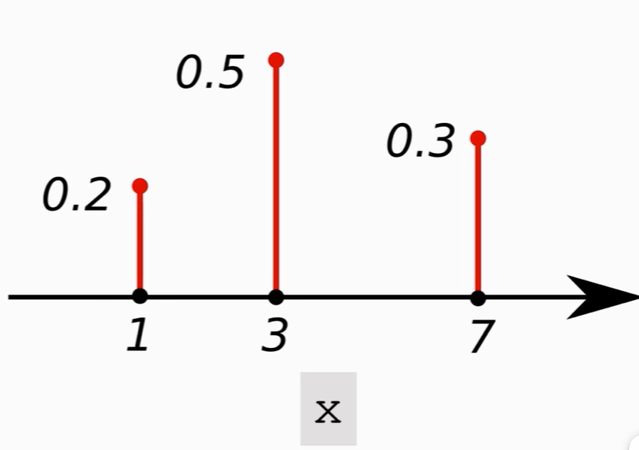
性质：

随机变量 X 作用域定义为花体 $\mathcal{X}$
如果 X 是连续的变量分布，则可对概率密度函数做定积分，值为1。
\[\int_{\mathcal{X}}p(x)dx=1 \]
如果 X 是离散的变量分布，则可对 p(x) 做一个加和，值为1。
\[\sum_{x\in \mathcal{X}}p(x) = 1 \]

c. 期望

对于作用域 $\mathcal{X}$ 中的随机变量 X
对于连续分布，函数 f(x) 的期望为：
\[\mathbb{E}[f(x)]=\int_{\mathcal{X}}p(x) \cdot f(x) dx \]
对于离散分布，函数$$f(x)$$的期望为：
\[\mathbb{E}[f(x)]=\sum_{x\in \mathcal{X}}p(x)\cdot f(x) \]
p(x) 是概率密度函数

d. 随机抽样

Random Sampling.

假设有10个球，2红，5绿，3蓝，随机抽一个球，会抽到哪个球？

在抽之前，抽到球的颜色就是个随机变量$$X$$，有三种可能取值红\绿\蓝。抽出一个球，是红色，这时候就有了一个观测值 x 。上述过程就叫随机抽样

换一个说法：

箱子里有很多个球，也不知道有多少个。做随机抽样，抽到红色球概率是0.2，绿色球概率是0.5，蓝色球概率是0.3。抽一个球，记录颜色，然后放回去摇匀，重复一百次，大概会有20个是红色，50个是绿色，蓝色有30个。这样就有统计意义。

模拟一下过程：

from numpy.random import choice
# choice函数用于抽样
samples = choice(['R','G','B'], size = 100, p = [0.2, 0.5, 0.3])
print(samples)

# 输出为

['G' 'G' 'G' 'B' 'G' 'G' 'G' 'R' 'B' 'G' 'R' 'B' 'G' 'G' 'G' 'B' 'B' 'G'
 'G' 'G' 'R' 'R' 'R' 'G' 'B' 'G' 'R' 'B' 'R' 'G' 'R' 'G' 'B' 'B' 'G' 'G'
 'B' 'R' 'R' 'G' 'G' 'G' 'G' 'B' 'G' 'B' 'G' 'G' 'G' 'B' 'G' 'B' 'R' 'R'
 'G' 'G' 'B' 'B' 'G' 'G' 'B' 'B' 'R' 'G' 'G' 'G' 'B' 'B' 'G' 'G' 'B' 'G'
 'G' 'G' 'G' 'G' 'B' 'G' 'R' 'B' 'G' 'G' 'G' 'B' 'G' 'R' 'B' 'R' 'B' 'G'
 'G' 'B' 'G' 'R' 'G' 'G' 'G' 'G' 'G' 'G']

1.2 强化学习术语 / Terminologies

a. state与action

假设在玩超级玛丽

状态state $$s$$ 可以表示为当前游戏这一帧的画面

观测到状态后可以做出相应动作action $$ a \in {{left, right, up} }$$

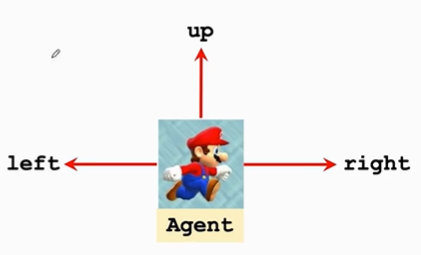
这个例子中马里奥被称为agent，若在自动驾驶中，汽车就被称为agent。动作谁做的就被称为agent。

b. 策略policy

$policy \space \pi $，指根据观测到的状态，然后做出决策，来控制 agent 运动。$$\pi$$是一个概率密度函数。

数学定义：$\pi :(s,a) \mapsto [0,1]:$$\pi(a|s) = \mathbb{P}(A=a|S=s)$
意思给定状态 $s$，做出动作 $a$ 的概率密度
比如给定一个马里奥的运行状态图
$\pi(left|s) =0.2$向左概率是0.2
$\pi(right|s)=0.1$向右概率是0.1
$\pi(up|s)=0.7$向上概率是0.7
如果让策略函数自动来操作，它就会做一个随机抽样，0.2的概率向左，0.1的概率向右，0.5的概率向上。
强化学习就是学习这个策略函数。
给定观测到的状态state $S=s$，agent的action $A$可以是随机的(最好是随机)

c. 奖励reward

agent做出一个动作，游戏就会给一个奖励，奖励通常需要自己来定义。奖励定义好坏非常影响强化学习结果。

例如在马里奥例子中：

马里奥吃到一个金币：$R=+1$。
赢了这场游戏：$R=+10000$。
碰到敌人 goomba，game over：$R=-10000$。
啥也没发生：$R=0$。

强化学习目标就是奖励获得的总额尽量要高。

d. 状态转移 state transition

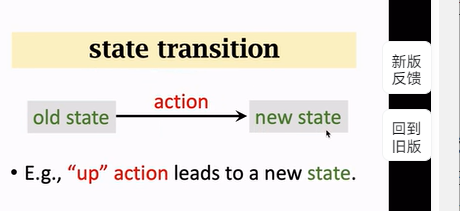
当前状态下，马里奥做一个动作，游戏就会给出一个新的状态。比如马里奥跳一下，屏幕当前帧就不一样了，也就是状态变了。这个过程就叫状态转移。

状态转移可以确定的也可以是随机的。
状态转移的随机性来自于环境，这里环境就是游戏的程序，程序决定下一个状态是什么。
状态转移函数：$p(s'|s,a)=\mathbb{P}(S'=s'|(S=s,A=a))$
意为观测到当前状态 $s$ 与动作 $a$ ，$p$ 函数输出状态 $s'$ 的概率。
如果马里奥向上跳后，goomba向左和向右的概率分别是0.8和0.2，这个状态转移函数只有环境知道，玩家是不知道的。

e. 交互

agent environment interaction.

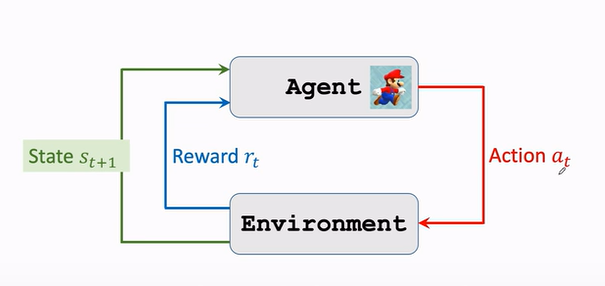
环境告诉Agent一个状态$s_t$
agent看到状态$$s_t$$之后，做出一个动作$a_t$
agent做出动作后，环境会更新状态为$s_{t+1}$，同时给出一个奖励$r_t$。

1.3 强化学习中的随机性

随机性有两个来源：

agent动作的随机性
状态转移的随机性

第一个随机性是从agent动作来的，因为动作是根据 policy 函数随机抽样得来的。

$\pi(left / s)=0.2$
$\pi(right / s)=0.1$
$\pi(up / s)=0.7$
agent可能做其中任何一个中动作，但动作概率有大有小。

另一个随机性来源是状态转移。

假定agent做出一个动作，那么环境就要生成一个新状态$S'$。
环境用状态转移函数 $p$ 算出概率，然后用概率来随机抽样来得到下一个状态

1.4 用AI玩游戏

通过强化学习得到的 policy 函数$\pi$，来控制 agent：

观测到当前的状态 s₁
ai 通过 policy 函数随机抽样做出动作 a₁（例子中的左、右、上）
environment 会生成一个下一个状态 s₂，并给 agent 一个奖励 r₁
ai 继续以新的状态作为输入，生成下一个动作 a₂
.......
循环直到游戏结束（赢或者输）

通过上面的步骤可以得到一个 (state, action, reward) 轨迹Trajectory（序列）：

s1,a1,r1,s2,a2,r2,⋯,st,at,rt

1.5 Reward && Return

Reward 在上面介绍过， Return 是 Reward 的线性组合。

a. Return 的定义

Return 回报，又被称为cumulative future reward，未来的累计奖励

\[U_t = R_t+R_{t+1}+R_{t+2}+\cdots \]

把从 t 时刻开始的奖励全都加起来，一直加到游戏结束的最后一个奖励。

不过我们要想一个事情：

对于 U_t 而言，R_t 和 R_t+1 同样重要吗？

假设有两个选项
- 立马给你一百块
- 一年后给你一百块

一般大多数人会选立刻拿到100块，因为未来的不确定性很大。

如果改成现在给你80，或者一年后给你100块，这时候就不像上面那么肯定了。

这说明， U_t 的各个求和项，未来的奖励不如现在的奖励好，应当打一个折扣。即：R_t+1 的权重Weights 要小于 R_t。

所以我们针对这个考虑进行一个调整，对 R_t+1 以后进行一个权重调整，也即强化学习中的 Discounted Return.

Discounted Return，折扣回报，也被称为：cumulative discounted future reward

折扣率称为 $\gamma$，该值介于0到1之间，是一个超参数，决定未来回报的重要程度。
调整之后的 Return 为：
\[U_t=R_t+\gamma R_{t+1}+\gamma^2 R_{t+2}+\gamma^3 R_{t+3}+\cdots \]

关于公式的字母表达问题：
假如游戏已经结束了，所有的奖励都观测到了，那么奖励就都是数值，用小写 r 表示。
如果在 t 时刻游戏还没有结束，这些奖励就还都是随机变量，就用大写字母 R 来表示奖励。
回报 U 依赖于奖励 R，所以它也是个随机变量，也要用大写字母表示。

b. 回报的随机性 Randomness in Returns

$U_t = R_t + \gamma{}R_{t+1}+\gamma^2 R_{t+2} + \gamma^3 R_{t+3} + ...$

上面1.3 提到随机性有两个来源:

动作是随机的
$\mathbb{P}[A=a|S=s]=\pi(a|s)$
下一个状态是随机的
$\mathbb{P} [S'=s'|S=s,A=a]=p(s'|s,a)$

对于任意时刻的 $ i\geq t$，奖励 $R_i$ 取决于 $S_i$ 和 $$A_i$$，而回报 $U$ 又是未来奖励的总和。

因此，观测到 t 时刻状态 $s_t$，回报 $U_t$ 就依赖于如下随机变量

$ A_t, A_{t+1}, A_{t+2},\cdots $$和 $$S_{t+1},S_{t+2},\cdots$

1.6 价值函数

a. 由来

Action-Value Function $Q(s,a)$

上面说到Discounted Return 折扣回报，cumulative discounted future reward

$U_t=R_t+\gamma R_{t+1}+\gamma^2 R_{t+2}+\gamma^3 R_{t+3}+\cdots$

$U_t$是个随机变量，在 t 时刻并不知道它的值是什么，那如何评估当前形势？

可以对$$U_t$$求期望，把里面的随机性都给积掉，得到的就是个实数。打个比方就是抛硬币之前，不知道结果是什么，但知道正反面各有一半的概率，正面记作1，反面记作0，得到的期望就是0.5。

同样对 $U_t$ 求期望，就可以得到一个数，记作 $Q_\pi$

这个期望怎么求的？

把 $U_t$ 当作未来所有动作 $A$ 和状态 $S$ 的一个函数，未来动作 $A$ 和状态 $S$ 都有一个随机性；
动作 $A$ 的概率密度函数是策略函数（policy函数）
$ \mathbb{P}(A=a|S=s) = \pi(a|s)$ ；
状态$$S$$的概率密度函数是状态转移函数 $\mathbb{P}(S'=s'|S=s,A=a) = p(s'|s,a)$
期望就是对这些 $A$ 和 $S$ 求的，把这些随机变量都用积分给积掉，这样除了 $S_t$ 与 $A_t$，其余所有的随机变量 ($A_{t+1},A_{t+2},\cdots$ 和 $S_{t+1},S_{t+2},\cdots$) 都被积掉了。

求期望得到的函数就被称为动作价值函数

$Q_\pi(s_t,a_t)=\mathbb{E}[U_t | S_t=s_t,A_t = a_t]$.

价值函数依赖于什么呢？
1. $S_t$ 和 $A_t$
  $S_t$ 与 $A_t$ 被当作被作为观测到的数值来对待，而不是随机变量，所以没有被积分积掉。 $$Q_\pi$$ 的值依赖于 $S_t$ 和 $A_t$ 。
2. 策略函数 Policy
  积分的时候会用到 Policy 函数$\pi$。

b. 动作价值函数

Action-value function.

对于策略 $\pi$，动作价值函数定义如下

$Q_\pi(s_t,a_t) = \mathbb{E}[U_t|S_t=s_t,A_t=a_t]$
- $Q_\pi$依赖于当前动作$a_t$与状态$s_t$，还依赖于策略函数$\pi$ (积分时会用到它，$\pi$不一样，得到的$Q_\pi$就不一样)。
- 直观意义：如果用策略函数$\pi$，那么在$s_t$这个状态下做动作$a_t$，是好还是坏。它会给当前状态下每个动作打分，这样就知道哪个动作好那个动作差。

动作价值函数依赖于$\pi$，那么如何去掉 $\pi$ ?

可以对 $Q_\pi$ 关于 $\pi$ 求最大化。意思就是可以有无数种策略函数 $\pi$，但我们要采用最好的那一种策略函数，即让 $Q_\pi$ 最大化的那个函数。

$Q_{\pi}$最大化的那个函数为：最优动作价值函数 Optimal action-value Function 。

$Q^*(s_t,a_t) = \mathop{max}\limits_{\pi}Q_\pi(s_t,a_t)$
直观意义：对动作 a 做评价，如果当前状态是 $s_t$，$Q*$ 会告诉我们动作 $a_t$ 好不好。agent就可以拿 Q* 对动作的评价来作决策。

c. 状态价值函数

State-value function. 状态价值函数 $V_\pi$是动作价值函数$Q_\pi$的期望。

$V_π(s_t)=E_A[Q_π(s_t,A)]$
而$Q_\pi$ 与策略函数 $\pi$ ，状态 $s_t$ 和动作 $a_t$ 都有关，可以将 A 作为随机变量，对 A 求期望消掉 A, 这样 $V_\pi$ 就只与 $\pi$ 和 $s$ 有关。

直观意义：告诉我们当前局势好不好，比如下围棋，当前是快赢了还是快输了。评价的是当前的 state。

这里期望是关于随机变量 A 求的，它的概率密度函数是

$π(⋅∣s_t)$，根据期望定义（线性可加性），可以写成连加或者积分的形式。

如果动作是离散的，如上下左右：

$V_\pi(s_t) = \mathbb{E_A}[Q_\pi(s_t,A)]=\sum_a\pi(a|s_t)\cdot{Q_\pi}(s_t,a)$
这里动作是离散的。

如果动作是连续的，如方向盘角度，从正90度到负90度。

$V_\pi(s_t) = \mathbb{E_A}[Q_\pi(s_t,A)]=\int\pi(a|s_t)\cdot {Q_\pi}(s_t,a)da$
这里动作是连续的

d. 总结

动作价值函数$Q_\pi(s_t,a_t) = \mathbb{E}[U_t|S_t=s_t,A_t=a_t]$
它跟策略函数 $\pi$，状态 $s_t$，动作 $a_t$有关，是 $U_t$ 的条件期望。
能告诉我们处于状态 s 时采用动作 a 是否明智，可以给动作 a 打分。
状态价值函数$V_{\pi}(s_t) = \mathbb{E}_A[Q_\pi(s_t,A)]$
它是把$Q_\pi$中把 A 用积分给去掉，这样变量就就只剩状态 s 。它跟策略函数 $\pi$，状态 $s_t$ 有关，跟动作 $a_t$ 无关。
能够评价当前局势是好是坏，也能评价策略函数的好坏，如果 $\pi$ 越好，则 $V_\pi$ 期望值$\mathbb{E}_S[V_\pi(S)]$越大。

1.7 如何用强化学习玩游戏

a. 两种学习方式

假设在马里奥游戏中，目标在于尽可能吃金币，避开敌人，通关。如何做？

一种是学习一个策略函数 $\pi(a|s)$，这叫 policy basement learning 策略学习，然后基于此来控制agent做动作。
每观测到一个状态 $s_t$，就把 $s_t$ 作为 $\pi(\cdot|s)$ 函数输入，$\pi$ 函数输出每一个动作的概率，基于概率来随机采样获取动作 $a_t$，让agent 来执行这个$a_t$。
另一种是学习最优动作价值函数$Q^*(s,a)$，这叫 value basement learning 价值学习，它告诉如果处于状态s，做动作a是好还是坏。
每观测到一个状态 $s_t$，把 $s_t$ 作为 $Q^*(s,a)$ 函数输入，让 $Q^*(s,a)$ 对每一个动作做一个评价，得到每个动作的 Q 值。选择输出值最大的动作，$a_t = argmax_a Q^*(s_t,a)$，因为 Q 值是对未来奖励总和的期望，如果向上动作 Q 值比其他动作 Q 值要大就说明向上跳的动作会在未来获得更多的奖励。

b. OpenAI Gym

OpenAI Gym https://gym.openai.com 是强化学习最常用的标准库。如果得到了 $\pi$ 函数或者 $Q*$ 函数，就可以用于Gym的控制问题和小游戏，来测试算法的优劣。

按照官方文档，安装 gym，就可以用 python 调用 gym 的函数。

安装 gym 想专门另开一篇笔记来记录，目前跑视频教程里的demo还是可以的。

简易安装过程：

pip install gym==0.15.7 -i http://mirrors.aliyun.com/pypi/simple --trusted-host mirrors.aliyun.com

截止2022-07-03，gym最新版本是0.21，但由于我的 python 环境为 3.6.4，所以我的 gym版本需要下降。

我的 pip 最近总是连接不到远端库，执行pip install 库会报错：
Retrying (Retry(total=0, connect=None, read=None, redirect=None, status=None))
after connection broken by 'SSLError(SSLError(1, u'[SSL: CERTIFICATE_VERIFY_FAI
LED] certificate verify failed (_ssl.c:726)'),)': /packages/0f/fb/6aecd2c8c9d0ac
83d789eaf9f9ec052dd61dd5aea2b47ffa4704175d7a2a/psutil-5.4.8-cp27-none-win_amd64.
whl
python使用pip安装模块出错 Retrying (Retry(total=0, connect=None, read=None, redirect=None, status=None)) - Aimed - 博客园 (cnblogs.com)
所以需要命令行后面的部分。

然后其他的东西我还没有装。如果装了会更新在安装笔记里。参考教程为：

c. gym 例程

import gym
import time
# 生成 CartPole 环境
env = gym.make('CartPole-v0')

# 重置环境
state = env.reset()

# 这里的循环就是上面 s,a,r的过程
for t in range(10000):
    # 弹出窗口来显示游戏情况
    env.render()
    print(state)

    # 随机均匀抽样一个动作记为 action
    # 这里是为了图方便，实际应用应该通过policy函数或者Q*来选择。
    action = env.action_space.sample()
    
    # 把action输入到step()函数,即agent执行这个动作
    state,reward,done,info = env.step(action)
    # 为了不让窗口太快消失
    time.sleep(1)
    if done:
        print("Finished")
        break


env.close()

运行效果：