Introduction to tree and binary tree

Basic concepts related to trees

Trees ：
Tree is a kind of nonlinear data structure , It is from n（n>=0） Finite nodes make up a set with hierarchical relations . It's called a tree because it looks like an upside down tree , That is to say, it is root up , And leaf down .
There is a special node , It's called the root node , The root node has no precursor node . Except for the root node , The rest of the nodes are divided into M(M>0) Disjoint sets T1、T2、……、Tm, And every set of them Ti(1<= i <= m) It is also a subtree with a structure similar to that of a tree . The root node of each subtree has and only has one precursor , There can be 0 One or more successors , therefore , Trees are defined recursively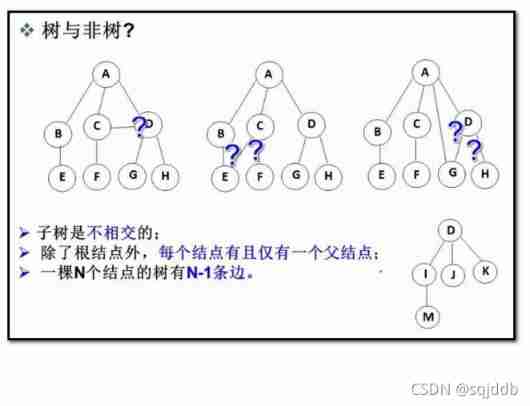

Degree of node ： The number of subtrees a node contains is called the degree of the node , Pictured above ：A The degree of 6
Leaf node or terminal node ： Degree is 0 A node of is called a leaf node
Non terminal node or branch node ： The degree is not for 0 The node of
Parent node or parent node ： If a node has child nodes , This node is called the parent of its child , Pictured above ：A yes B Parent node
Child node or child node ： The root node of the subtree that a node contains is called the child node of the node , Pictured above ：B yes A The child node of
Brother node ： Nodes with the same parent are called siblings ; Pictured above ：B、C It's a brother node
The degree of a tree ： In a tree , The degree of the largest node is called the degree of the tree ; Pictured above ： The degree of the tree is 6
Hierarchy of nodes ： Starting from the root , The root for the first 1 layer , The child node of the root is the 2 layer , And so on ;
The height or depth of a tree ： The maximum level of nodes in the tree ; Pictured above ： The height of the tree is 4
Cousin node ： The nodes of both parents on the same layer are cousins to each other ; Pictured above ：H、I Be brothers to each other
The ancestor of node ： From the root to all nodes on the branch through which the node passes ; Pictured above ：A Is the ancestor of all nodes
descendants ： Any node in a subtree with a node as its root is called the descendant of the node . Pictured above ： All nodes are A The descendants of
The forest ： from m（m>0） A collection of trees that do not intersect each other is called a forest ;

The representation of a tree

requirement ： Since the value field is saved , Also save the relationship between nodes
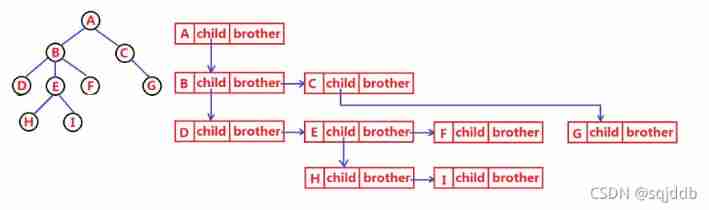
In practice, there are many representations of trees, such as ： Parenting , Child representation 、 The child's parent representation and the child's brother representation . Let's have a simple understanding of the most commonly used child brother representation .

typedef int DataType;
struct Node
{
    
   struct Node* _firstChild1; //  The first child node 
   struct Node* _pNextBrother; //  Point to its next sibling node 
   DataType _data; //  Data fields in nodes 
};

Related concepts of binary tree

Binary tree （Binary tree） It's an important type of tree structure . The data structure abstracted from many practical problems is often in the form of binary tree , Even ordinary trees can be transformed into binary trees , Moreover, the storage structure and algorithm of binary tree are relatively simple , So binary tree is very important . The characteristic of binary tree is that each node can only have two subtrees at most , And there are left and right sides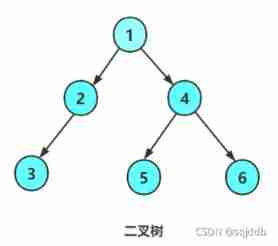

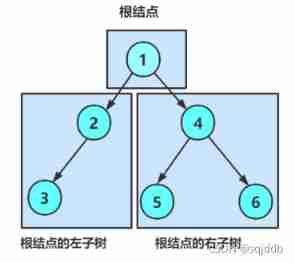
As can be seen from the above figure ：

1. The degree of nonexistence of binary trees is greater than 2 The node of

2. The subtree of a binary tree has left and right branches , The order cannot be reversed , So a binary tree is an ordered tree

3. Any binary tree is composed of the following cases

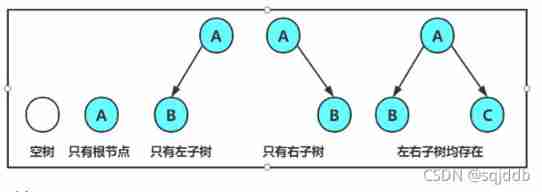
Special binary tree ：

1. Full binary tree ： A binary tree , If the number of nodes in each layer reaches the maximum , Then this binary tree is full of binary trees . in other words , If the number of layers of a binary tree is 2^K-1, And the total number of nodes is , Then it's full of binary trees .
2. Perfect binary tree ： The depth of a tree is one k There are n A binary tree of nodes , Click from top to bottom for the nodes in the tree 、 Number from left to right , If the number is i（1≤i≤n） The node and the full binary tree are numbered as i The nodes of the binary tree have the same position , This binary tree is called a complete binary tree .

Properties of binary trees

1. If the specified number of layers of the root node is 1, Then the second of a non empty binary tree i There is a maximum of 2^(i-1) Nodes .

2. If the specified number of layers of the root node is 1, Then the depth is h The number of nodes in a binary tree is the largest 2^h-1 .

3. * Any binary tree , If the degree is 0 The number of leaf nodes is n0 , Degree is 2 The number of branch nodes is n2 , Then there are n0＝n2 ＋1

4. If the specified number of layers of the root node is 1, have n The depth of a full binary tree of nodes ：
   

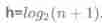
5. Those who have n Of nodes Perfect binary tree , If all nodes are in the array order from top to bottom and from left to right 0 Numbered starting , On the other hand
   The serial number is i There are ：
   if i>0,i The parent sequence number of the location node ：(i-1)/2;i=0,i Number the root node , No parent nodes
   if 2i+1<n, Left child serial number ：2i+1（2i+1>=n No left child ）
   if 2i+2<n, Right child number ：2i+2（2i+2>=n No right child ）

Binary tree storage structure

Binary trees can generally use two structures to store , A sequential structure , A chain structure

>> Sequential storage

Sequential structure storage is to use arrays to store , Generally, arrays are only suitable for representing complete binary trees , Because it is not a complete binary tree, there will be a waste of space . The sequential storage of binary tree is physically an array , Logically, it is a binary tree .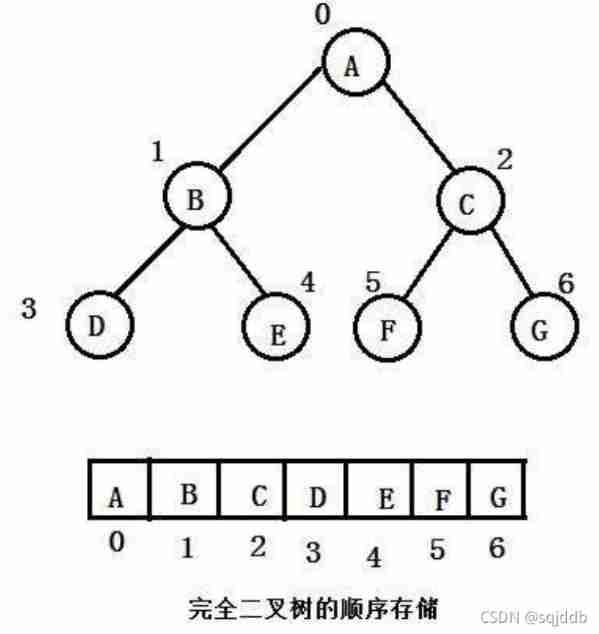
Sequential storage of incomplete binary tree ：
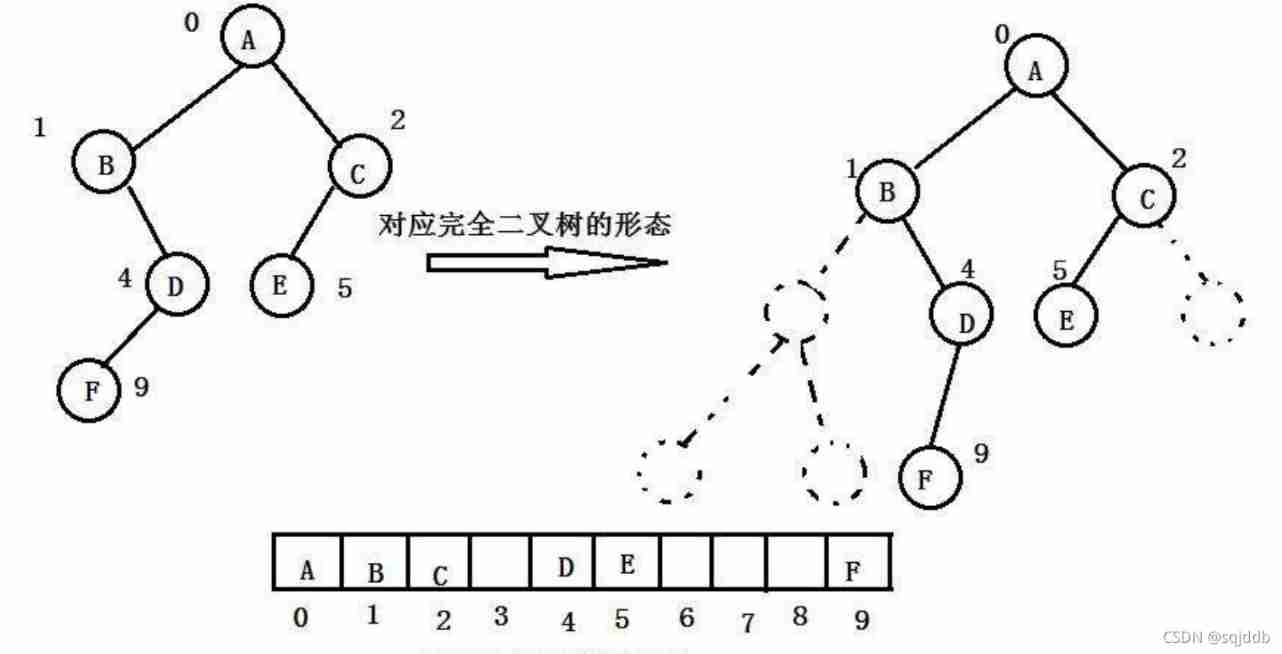Sequential structure is more suitable for storing complete binary trees . In reality, we usually regard Pile up Use an array of sequential structures to store

>> Heap storage

The heap is a complete binary tree
The heap with the largest root node is called the maximum heap or the large root heap , The heap with the smallest root node is called the minimum heap or the small root heap
The value of a node in the heap is always no greater than or less than the value of its parent node

Build the heap with the downward adjustment algorithm of the heap

Heap down adjustment algorithm
The downward adjustment algorithm has a premise ： The left and right subtrees must be a heap , To adjust
Take a small heap as an example to illustrate the algorithm process ：
Select the smaller value of the left and right children of the root node and compare it with the value of the root node , If the child is small , Swap the root node with the younger child , Then compare the smaller value of the left and right children with their parent nodes , The exchange rules are the same , Until the child is bigger than the father , The procedure is as follows ：

void adjustDown(int* a,int n,int parent)
{
    
  int child = parent*2+1;
  while(child<n)
  {
    
    // Choose the younger of the left and right children 
    if(child+1<n&&a[child+1]<a[child])
	  child++;
	  
	// Compare the selected child with the parent node 
	if(a[parent]<a[child])
	{
    
	  break;
	}
	else
	{
    
	  swap(&a[parent],&a[child]);
	  parent = child;
	  child = parent*2+1;
	}
	  
  }
}

Use this algorithm to adjust forward from the penultimate non leaf node of a complete binary tree , Until you adjust to the root node , The pile is built . It can be observed that the subscript of the first non leaf child node is (n-2)/2, The procedure of pile building is as follows

for(i=(n-2)/2;i>=0;i--)
   adjustDown(a,n,i);

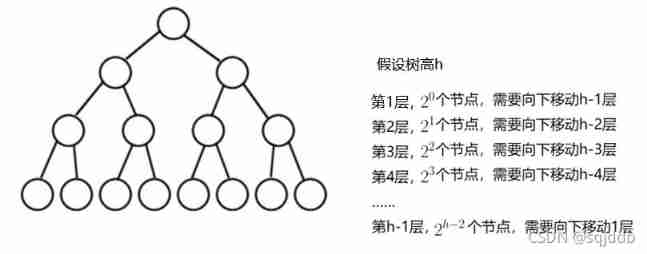
Time complexity of reactor building

Because the heap is a complete binary tree , A full binary tree is also a complete binary tree , In order to simplify, we use full binary tree to prove ( Time complexity is an approximation , Several more nodes do not affect the final result ）

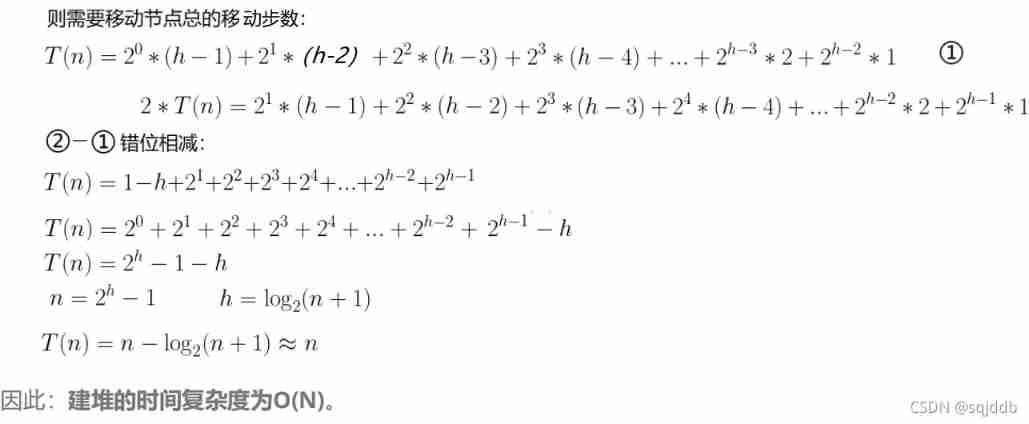
Basic operation of the heap

Pile insertion
First insert a 10 To the end of the array , Then adjust the algorithm upward , Until the heap .
Heap delete
Deleting the heap is to delete the data at the top of the heap , Replace the last data of the data root at the top of the heap , Then delete the last data of the array , Then adjust the algorithm downward .
Heap sort
The basic idea of heap sorting is ： The sequence to be sorted is constructed into a large top heap , here , The maximum value of the whole sequence is the root node at the top of the heap . Exchange it with the last element , At the end of this time is the maximum value . And then there will be the rest n-1 Elements are restructured into a heap , This will get n The minor value of an element . Do it over and over again , Then we can get an ordered sequence
TOPk problem
That is, before data combination K The largest element or the smallest element , Generally, the amount of data is relatively large .
such as ： Before major 10 name 、 The world 500 strong 、 Rich list 、 Before the game 100 Active players, etc .
about Top-K problem , The simplest and most direct way you can think of is to sort , however ： If the amount of data is very large , Sorting is not very desirable ( Probably
Data can't all be loaded into memory at once ). The best way is to use the heap to solve , The basic idea is as follows ：

1. Use the first... In the data set K Elements to build the heap
   front k The biggest element , Then build a small pile
   front k The smallest element , Then build a lot of
2. With the rest of N-K The elements are compared with the top elements in turn , If not, replace the heap top element

Will remain N-K After the elements are compared with the top elements in turn , The rest of the heap K The first element is the front K The smallest or largest element

Complete procedures for heap related operations

>> Chain store

The chain storage structure of binary tree refers to , Use linked list to represent a binary tree , Chain is used to indicate the logical relationship of elements . The usual method is that each node in the linked list consists of three fields , Data fields and left and right pointer fields , The left and right pointers are used to give the storage address of the chain node where the left child and the right child of the node are located . Chain structure can be divided into binary chain and trigeminal chain .

For the tree below ：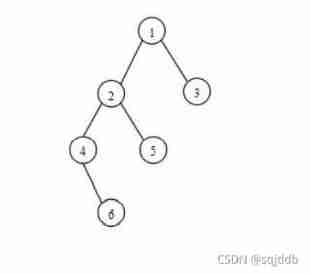

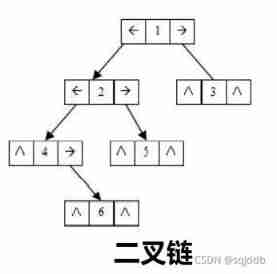
typedef int BTDataType;
//  Binary chain 
struct BinaryTreeNode
{
    
  struct BinTreeNode* _pLeft; //  Point to the left child of the current node 
  struct BinTreeNode* _pRight; //  Point to the right child of the current node 
  BTDataType _data; //  Current node value range 
}

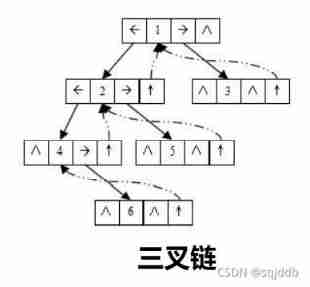
//  Trident chain 
struct BinaryTreeNode
{
    
   struct BinTreeNode* _pParent; //  Points to the parent of the current node 
   struct BinTreeNode* _pLeft; //  Point to the left child of the current node 
   struct BinTreeNode* _pRight; //  Point to the right child of the current node 
   BTDataType _data; //  Current node value range 
};

Traversal of binary tree

According to the rules , The traversal of binary tree has ： Before the order / Middle preface / The recursive structure of post order traverses ：

1. The former sequence traversal (Preorder Traversal Also called preorder traversal )—— The operation of accessing the root node occurs before traversing its left and right subtrees .

void PreOrder(BTNode* root) {
    
	if (root == NULL) {
    
		printf("NULL ");
		return;
	}

	printf("%c ", root->_data);
	PreOrder(root->_left);
	PreOrder(root->_right);
}

2. In the sequence traversal (Inorder Traversal)—— The operation of accessing the root node occurs in traversing its left and right subtrees （ between ）.

void InOrder(BTNode* root)
{
    
	if (root == NULL) {
    
		printf("NULL ");
		return;
	}

	InOrder(root->_left);
	printf("%c ", root->_data);
	InOrder(root->_right);
}

3. After the sequence traversal (Postorder Traversal)—— The operation to access the root node occurs after traversing its left and right subtrees .

void PostOrder(BTNode* root)
{
    
	if (root == NULL) {
    
		printf("NULL ");
		return;
	}

	PostOrder(root->_left);
	PostOrder(root->_right);
	printf("%c ", root->_data);
}

4. Sequence traversal
From top to bottom , The process of accessing the nodes of the tree layer by layer from left to right is sequence traversal .
The implementation of sequence traversal can use queues
The basic idea ： Root node data first The team , Get the team leader data Print , Root node data Out of the team , The left node of the root joins the queue , Then the right node joins the team , Take the data circularly, print it and leave the team , After each data is out of the queue, let its left and right node data enter the queue , The procedure is as follows ：

void BinaryTreeLevelOrder(BTNode* root)
{
    
	Queue q;
	QueueInit(&q);
	if (root)
	{
    
		QueuePush(&q, root);
	}

	while (!QueueEmpty(&q))
	{
    
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		printf("%c ", front->data);

		if (front->left)
		{
    
			QueuePush(&q, front->left);
		}

		if (front->right)
		{
    
			QueuePush(&q, front->right);
		}
	}

	printf("\n");

	QueueDestory(&q);
}

Classic program of binary tree chain structure

① Find the number of nodes in the binary tree
Here are two ways

Traverse ---- Global variable method ：

int size = 0;
void BinaryTreeSize(BTNode* root)
{
    
	if (root == NULL)
		return;
	else
		++size;

	BinaryTreeSize(root->left);
	BinaryTreeSize(root->right);
}

Divide and conquer method ：

int BinaryTreeSize(BTNode* root)
{
    
	return root == NULL ? 0 : 1 
		+ BinaryTreeSize(root->left) 
		+ BinaryTreeSize(root->right);
}

② Number of leaf nodes of binary tree

int BinaryTreeLeafSize(BTNode* root)
{
    
	if (root == NULL)
	{
    
		return 0;
	}
	else if (root->left == NULL && root->right == NULL)
	{
    
		return 1;
	}
	else
	{
    
		return BinaryTreeLeafSize(root->left)
			+ BinaryTreeLeafSize(root->right);
	}
}

③ The second fork is the tree k The number of layer nodes

int BinaryTreeLevelKSize(BTNode* root, int k)
{
    
	if (root == NULL)
		return 0;
	
	if (k == 1)
		return 1;

	return BinaryTreeLevelKSize(root->left, k - 1)
		+ BinaryTreeLevelKSize(root->right, k - 1);
}

④ The binary tree lookup value is x The node of

BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
    
	if (root == NULL)
		return NULL;
	
	if (root->data == x)
		return root;

	BTNode* retLeft = BinaryTreeFind(root->left, x);
	if (retLeft)
	{
    
		return retLeft;
	}
	
	BTNode* retRight = BinaryTreeFind(root->right, x);
	if (retRight)
	{
    
		return retRight;
	}

	return NULL;
    // I didn't find that I should return NULL, If you don't find it on the right, you'll find it back NULL
    // So the following part can be written like this 
	//return BinaryTreeFind(root->right, x);
}

⑤ Find the height of the binary tree / depth

int BinaryTreeDepth(BTNode* root)
{
    
	if (root == NULL)
	{
    
		return 0;
	}

	int leftDepth = BinaryTreeDepth(root->left);
	int rightDepth = BinaryTreeDepth(root->right);

	return leftDepth > rightDepth ? 
	leftDepth + 1 : rightDepth + 1;
}

There are many classic programs of binary tree , Unknown here , Pay attention to the application of multi sensory recursive method in binary tree .