当前位置:网站首页>7-8 7104 约瑟夫问题(PTA程序设计)
7-8 7104 约瑟夫问题(PTA程序设计)
2022-07-06 09:22:00 【编程林黛玉】
约瑟夫问题:有n只猴子,按顺时针方向围成一圈选大王(编号从1到n),从第1号开始报数,一直数到m,数到m的猴子退出圈外,剩下的猴子再接着从1 开始报数。就这样,直到圈内只剩下一只猴子时,这个猴子就是猴王,编程求输入n,m后,输出最后猴王的编号。
输入格式:
每行是用空格分开的两个整数,第一个是 n,第二个是m ( 0 < m, n < 300) 。最后一行是:0 0 。
输出格式:
对于每行输入数据(最后一行除外),输出数据也是一行,即最后猴王的编号。
输入样例:
6 2
12 4
8 3
0 0
输出样例:
5
1
7
代码(Python):
方法一:
n,m=map(int,input().split()) #输入n,m
list1=[] #用来存放“猴子”
list2=[] #用来存放最终结果
f=0 #一共有几组数
for i in range(300): #先在列表中增加元素,否则列表为空,无法对列表中的元素进行修改
list1.append(0)
while 1:
if n==0 and m==0: #输入“0 0”时,结束
break
else: #否则开始选猴王
for i in range(1,n+1): #因为猴子序列是从1开始的,所以我们的列表也从1开始
list1[i]=1 #先初始化列表中的数字使其全部为1,用1来表示未被淘汰的猴子
f+=1 #计数,一共算了几组数,最后作为list2的长度,用for输出结果
i=1 #从第一个数开始
sum=n #一开始时有n个1
count=0 #count就是1~m
while sum>1: #sum为n个数中1的个数,剩1个1时说明已经选出猴王
if list1[i]!=0: #对每一个不为0的数(未被淘汰的猴子),count+1
count+=1
if count==m: #直到count加到等于m的时候,使数到m的猴子退出圈外
count=0 #count又重新开始计数
list1[i]=0 #令对应的元素等于0,表示已经淘汰
sum-=1 #sum的个数减1,表示猴子个数少1
i+=1 #每淘汰完一只猴子,i加1,开始找下一只猴子
if i==n+1: #下标超过范围后,就返回开头找,相当于围成一个圈
i=1
for i in range(1,n+1): #遍历列表
if list1[i]!=0: #寻找不为0的数的位置,即猴王的序号
list2.append(i) #并将其序号加入结果列表中
n,m=map(int,input().split()) #再次输入,准备进入下一次循环
for i in range(f): #输出结果列表中的结果
print(list2[i])方法二:
n,m=map(int,input().split()) ##输入n,m
wang=[] #用来存放“猴子”
while 1:
if n==0 and m==0 : #输入“0 0”时,结束
break
else: #否则开始选猴王
k=0 #k表示报数额顺序,先将其置为0
wang.clear() #先将上一次的猴子序列清空
for i in range(1,n+1): #将n只猴子从1开始编号
wang.append(i)
while len(wang) > 1: #wang列表的长度大于1时,表示还未选出猴王,进入循环
i=0
while i<len(wang): #遍历王列表中的所有猴子
k+=1 #从第1号开始报数,一直数到m,每报一次数k加1
if k == m: #当k加到m时,表示该只猴子刚好数到m
del wang[i] #淘汰该猴子,即将它从列表中删去
k=0 #剩下的猴子再接着从1 开始报数,所以先将k置为0
#注意,当数到m时,将该猴子删除,于是它后面的猴子序号都将减一,所以i不需要加1就可以直接判断下一只猴子
else: #如果k不等于m,则该猴子不淘汰,使i加1,开始判断下一次猴子
i+=1
a=wang[0] #最后,退出了while循环,那一定是只剩下一只猴子了,即为猴王
print(a) #由于一开始存在wang列表中的就是各个猴子的序号,所以直接输出里面的值即为猴子的序号
n,m=map(int,input().split()) #再次输入,准备进入下一次循环思路:上面提供了两种解决该问题的方法,实质上是差不多的,都是通过一个列表存“猴子”,然后逐渐淘汰被选中的猴子,最终找到猴王。区别在于,在方法一中,先将列表里都存数据“1”来表示未被淘汰的猴子,然后数到m的猴子被置0表示淘汰,最终列表中只剩一个“1”时,表示选出猴王。在方法二中,列表中直接存入猴子的序号,然后将数到m的猴子直接从列表中删掉,最终列表中剩下的唯一一个元素就是猴王。
上面的程序给出了比较详细的注释,以便新手小白参考。程序的思路设计或者代码实现并不是最优的,欢迎各位大佬指正错误或者给出更优质的思路。
我是一只想成为鲲鹏的菜鸟,大家的鼓励是我前进的动力,欢迎大家点赞收藏评论哦!
边栏推荐
- 仿牛客技术博客项目常见问题及解答(一)
- Thoroughly understand LRU algorithm - explain 146 questions in detail and eliminate LRU cache in redis
- C语言入门指南
- [the Nine Yang Manual] 2020 Fudan University Applied Statistics real problem + analysis
- 简单理解ES6的Promise
- 1. C language matrix addition and subtraction method
- About the parental delegation mechanism and the process of class loading
- 4. Branch statements and loop statements
- 5. Download and use of MSDN
- 3. C language uses algebraic cofactor to calculate determinant
猜你喜欢
SRC挖掘思路及方法
The latest tank battle 2022 - Notes on the whole development -2

仿牛客技术博客项目常见问题及解答(二)
canvas基础1 - 画直线(通俗易懂)
FAQs and answers to the imitation Niuke technology blog project (I)
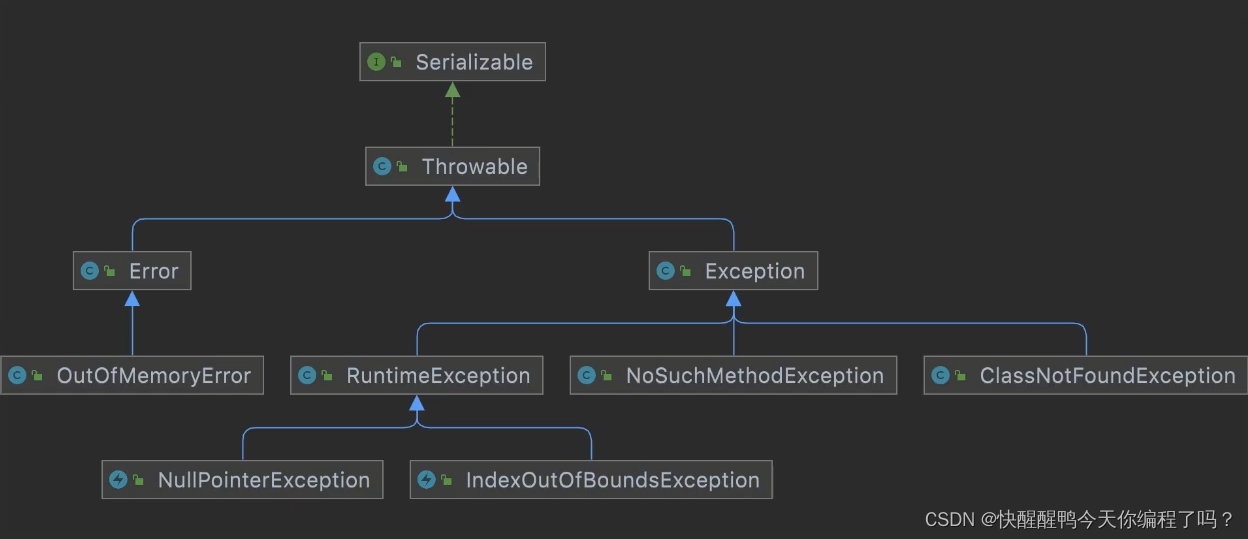
受检异常和非受检异常的区别和理解
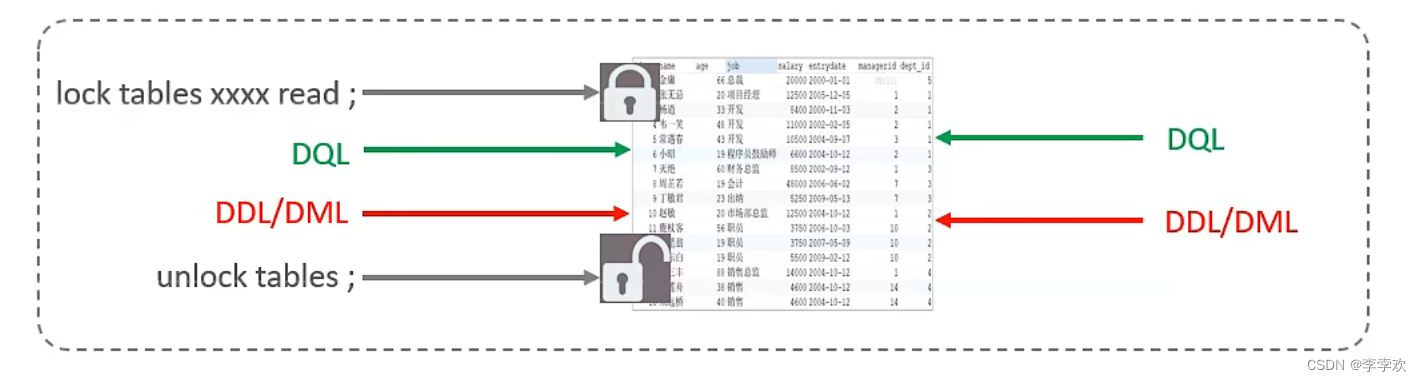
MySQL lock summary (comprehensive and concise + graphic explanation)

1.C语言初阶练习题(1)
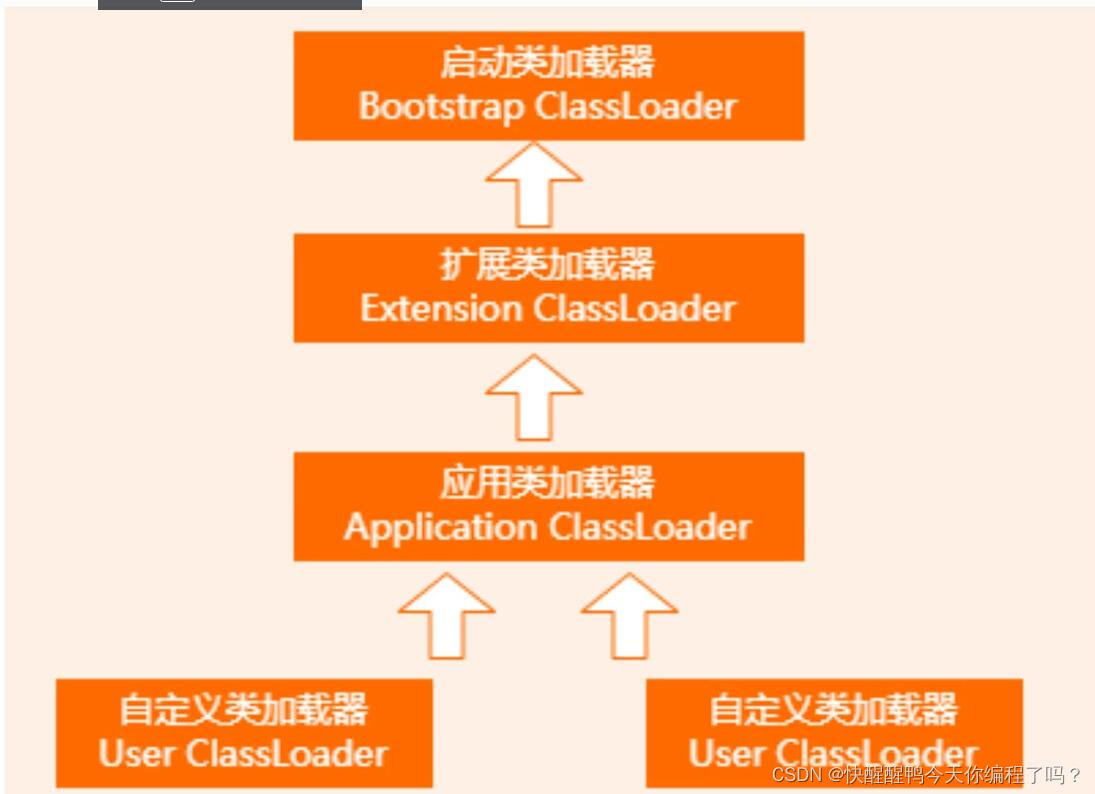
关于双亲委派机制和类加载的过程
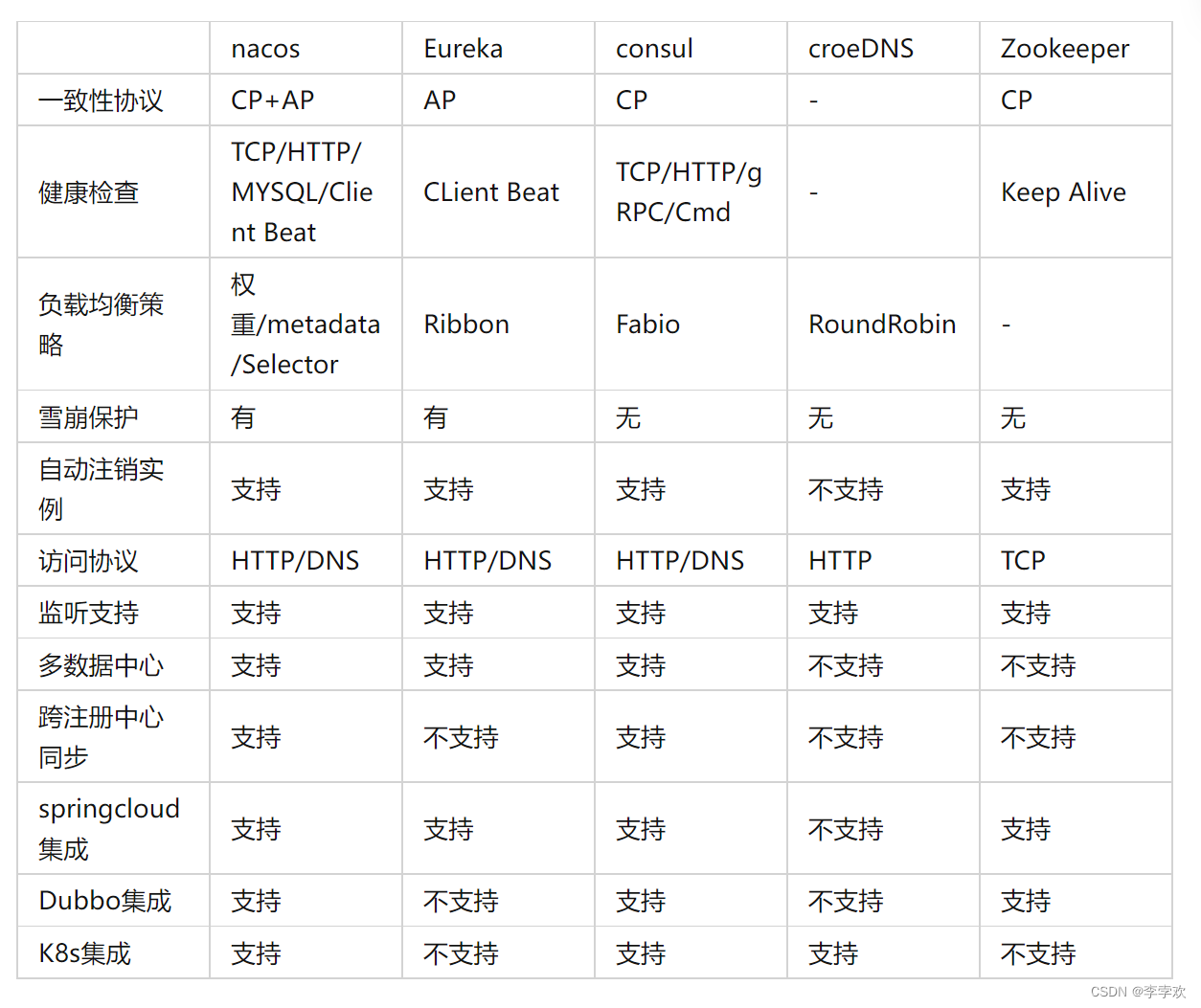
自定义RPC项目——常见问题及详解(注册中心)
随机推荐
canvas基础1 - 画直线(通俗易懂)
FAQs and answers to the imitation Niuke technology blog project (I)
3. Number guessing game
FAQs and answers to the imitation Niuke technology blog project (II)
Implement queue with stack
重载和重写的区别
The latest tank battle 2022 - full development notes-3
MySQL事务及实现原理全面总结,再也不用担心面试
Differences among fianl, finally, and finalize
Leetcode. 3. Longest substring without repeated characters - more than 100% solution
深度强化文献阅读系列(一):Courier routing and assignment for food delivery service using reinforcement learning
魏牌:产品叫好声一片,但为何销量还是受挫
Change vs theme and set background picture
[面试时]——我如何讲清楚TCP实现可靠传输的机制
Have you encountered ABA problems? Let's talk about the following in detail, how to avoid ABA problems
2.C语言矩阵乘法
【九阳神功】2017复旦大学应用统计真题+解析
[the Nine Yang Manual] 2016 Fudan University Applied Statistics real problem + analysis
canvas基础2 - arc - 画弧线
Mortal immortal cultivation pointer-1