当前位置:网站首页>[combinatorial mathematics] pigeon nest principle (simple form examples of pigeon nest Principle 4 and 5)
[combinatorial mathematics] pigeon nest principle (simple form examples of pigeon nest Principle 4 and 5)
2022-07-03 10:38:00 【Programmer community】
List of articles
- One 、 Example of simple form of pigeon nest principle 4
- Two 、 Example of simple form of pigeon nest principle 5
One 、 Example of simple form of pigeon nest principle 4
Suppose there is
3
3
3 individual
7
7
7 Bit binary number ,
A
:
a
1
a
2
a
3
a
4
a
5
a
6
a
7
A : a_1a_2a_3a_4a_5a_6a_7
A:a1a2a3a4a5a6a7
B
:
b
1
b
2
b
3
b
4
b
5
b
6
b
7
B : b_1b_2b_3b_4b_5b_6b_7
B:b1b2b3b4b5b6b7
C
:
c
1
c
2
c
3
c
4
c
5
c
6
c
7
C : c_1c_2c_3c_4c_5c_6c_7
C:c1c2c3c4c5c6c7
Prove the existence of an integer
i
i
i and
j
j
j ,
1
≤
i
≤
j
≤
7
1\leq i \leq j \leq 7
1≤i≤j≤7 , So that one of the following must be true :
a
i
=
a
j
=
b
i
=
b
j
a_i = a_j = b_i = b_j
ai=aj=bi=bj
a
i
=
a
j
=
c
i
=
c
j
a_i = a_j = c_i = c_j
ai=aj=ci=cj
b
i
=
b
j
=
c
i
=
c
j
b_i = b_j = c_i = c_j
bi=bj=ci=cj
prove :
Binary number , The value can only be
0
0
0 or
1
1
1 ;
Use table graphics to represent
A
B
C
ABC
ABC Three binary numbers
7
7
7 position : Use binary numbers
0
,
1
0,1
0,1 Fill in these digits ;

Above picture :
- The first
1
1
1 Line is Binary numbers
A
A
A Of
7
7
7 position ;
- The first
2
2
2 Line is Binary numbers
B
B
B Of
7
7
7 position ;
- The first
3
3
3 Line is Binary numbers
C
C
C Of
7
7
7 position ;
Use binary numbers
0
,
1
0,1
0,1 Fill in these digits in the form ;
Summarize the following patterns : In columns , Summarize certain patterns , The... Of each column in the following pattern
1
∼
3
1 \sim 3
1∼3 The row value is a certain number ;
①
1
−
2
−
0
1-2-0
1−2−0 : A column The first
1
1
1 That's ok , The first
2
2
2 That's ok , The value is
0
0
0 , The first
3
3
3 The row value is optional ;

②
1
−
2
−
1
1-2-1
1−2−1 : A column The first
1
1
1 That's ok , The first
2
2
2 That's ok , The value is
1
1
1 , The first
3
3
3 The row value is optional ;

③
1
−
3
−
0
1-3-0
1−3−0 : A column The first
1
1
1 That's ok , The first
3
3
3 That's ok , The value is
0
0
0 , The first
2
2
2 The row value is optional ;

④
1
−
3
−
1
1-3-1
1−3−1 : A column The first
1
1
1 That's ok , The first
3
3
3 That's ok , The value is
1
1
1 , The first
2
2
2 The row value is optional ;

⑤
2
−
3
−
0
2-3-0
2−3−0 : A column The first
2
2
2 That's ok , The first
3
3
3 That's ok , The value is
0
0
0 , The first
1
1
1 The row value is optional ;

⑥
2
−
3
−
1
2-3-1
2−3−1 : A column The first
2
2
2 That's ok , The first
3
3
3 That's ok , The value is
1
1
1 , The first
1
1
1 The row value is optional ;

There are more than that
6
6
6 There are two possible models , But binary numbers have
7
7
7 position ;
It can be understood equivalently as the pigeon nest principle : take
7
7
7 Put an object in
6
6
6 In a box , be At least one box contains
2
2
2 individual or
2
2
2 More than objects ;
So at least there is
2
2
2 Column or
2
2
2 The mode above is the same ;
In two columns with the same pattern , There are also rectangles with the same four corners , The number of four corner squares meets the same requirements ;
therefore , There must be an integer
i
i
i and
j
j
j ,
1
≤
i
≤
j
≤
7
1\leq i \leq j \leq 7
1≤i≤j≤7 , So that one of the following must be true :
a
i
=
a
j
=
b
i
=
b
j
a_i = a_j = b_i = b_j
ai=aj=bi=bj
a
i
=
a
j
=
c
i
=
c
j
a_i = a_j = c_i = c_j
ai=aj=ci=cj
b
i
=
b
j
=
c
i
=
c
j
b_i = b_j = c_i = c_j
bi=bj=ci=cj
Two 、 Example of simple form of pigeon nest principle 5
prove :
1
1
1 To
2
n
2n
2n In the positive integer of , Take whatever you like
n
+
1
n + 1
n+1 Number , At least a couple of them , One number is a multiple of the other number ;
Use the following form to express
1
1
1 To
2
n
2n
2n The positive integer ;
Each of the above numbers , Divide
2
α
i
2^{\alpha_i}
2αi , You will get an odd number
r
i
r_i
ri ;
Use
a
i
=
2
α
i
r
i
a_i = 2^{\alpha_i}r_i
ai=2αiri ,
i
=
1
,
2
,
⋯
,
n
+
1
i = 1, 2, \cdots , n+1
i=1,2,⋯,n+1 The form represents the above
1
1
1 To
2
n
2n
2n The positive integer ;
1
1
1 To
2
n
2n
2n A positive integer of indicates that : ( Just for your reference )
- It means odd : Odd number
r
i
r_i
ri It is equal to the positive integer value represented ,
2
α
i
=
1
2^{\alpha_i} = 1
2αi=1 , namely
α
i
=
0
\alpha_i = 0
αi=0 ;
- It means even number : If it's even , It can be divided by at least one
2
2
2 ,
2
α
i
≥
2
2^{\alpha_i} \geq 2
2αi≥2 , namely
α
i
≥
1
\alpha_i \geq 1
αi≥1 ;
1
1
1 To
2
n
2n
2n The positive integer in , Yes
n
n
n An odd number , yes
1
,
3
,
5
,
7
,
9
,
⋯
,
2
n
−
1
1, 3, 5, 7, 9, \cdots , 2n - 1
1,3,5,7,9,⋯,2n−1 ;
Number of each
a
i
=
2
α
i
r
i
a_i = 2^{\alpha_i}r_i
ai=2αiri On the right side of the
r
i
r_i
ri Odd number The value is only
n
n
n Kind of , On the right of the even part
r
i
r_i
ri Odd numbers are also included ;
Now from
1
1
1 To
2
n
2n
2n The positive integer in take
n
+
1
n+1
n+1 Number , If there are odd numbers , There must be only
n
n
n Species value ;
Think of values as boxes , On the right of each number
r
i
r_i
ri As an object , The number of odd numbers is
n
+
1
n + 1
n+1 individual , But the number of odd numbers is only
n
n
n Species value , So there are two numbers Odd parts
r
i
r_i
ri It's equal ;
Suppose these two numbers are respectively
i
i
i Number , And the
j
j
j Number :
r
i
=
r
j
r_i = r_j
ri=rj , also
i
<
j
i < j
i<j ;
- The first
i
i
a
i
=
2
α
i
r
i
a_i = 2^{\alpha_i}r_i
ai=2αiri ,
i
=
1
,
2
,
⋯
,
n
+
1
i = 1, 2, \cdots , n+1
i=1,2,⋯,n+1
i Number :
- The first
j
j
a
j
=
2
α
j
r
j
a_j = 2^{\alpha_j}r_j
aj=2αjrj ,
j
=
1
,
2
,
⋯
,
n
+
1
j = 1, 2, \cdots , n+1
j=1,2,⋯,n+1
j Number :
If
r
i
=
r
j
r_i = r_j
ri=rj , that
2
α
j
2^{\alpha_j}
2αj Must be
2
α
i
2^{\alpha_i}
2αi Multiple ;
边栏推荐
- Leetcode skimming ---263
- Model selection for neural network introduction (pytorch)
- Linear regression of introduction to deep learning (pytorch)
- Tensorflow - tensorflow Foundation
- Ut2015 learning notes
- Leetcode刷题---283
- [LZY learning notes dive into deep learning] 3.4 3.6 3.7 softmax principle and Implementation
- Drop out (pytoch)
- Configure opencv in QT Creator
- QT creator uses OpenCV Pro add
猜你喜欢

Install yolov3 (Anaconda)
ECMAScript--》 ES6语法规范 ## Day1
深度学习入门之线性回归(PyTorch)
重写波士顿房价预测任务(使用飞桨paddlepaddle)

【SQL】一篇带你掌握SQL数据库的查询与修改相关操作

Ut2014 supplementary learning notes

Handwritten digit recognition: CNN alexnet

A complete answer sheet recognition system
2018 Lenovo y7000 black apple external display scheme
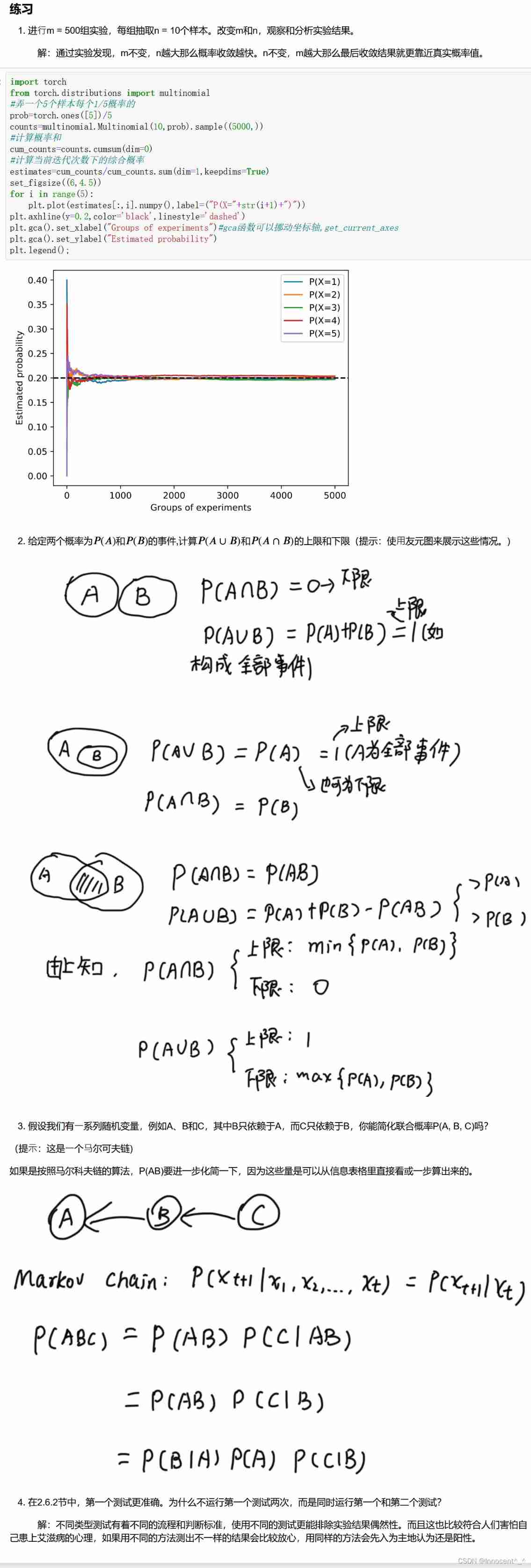
Hands on deep learning pytorch version exercise solution - 2.6 probability
随机推荐
Seata分布式事务失效,不生效(事务不回滚)的常见场景
权重衰退(PyTorch)
八、MySQL之事务控制语言
Tensorflow—Neural Style Transfer
Simple real-time gesture recognition based on OpenCV (including code)
High imitation Netease cloud music
安装yolov3(Anaconda)
Policy Gradient Methods of Deep Reinforcement Learning (Part Two)
Model selection for neural network introduction (pytorch)
Realize an online examination system from zero
Leetcode刷题---852
OpenCV Error: Assertion failed (size.width>0 && size.height>0) in imshow
熵值法求权重
七、MySQL之数据定义语言(二)
A super cool background permission management system
Configure opencv in QT Creator
Training effects of different data sets (yolov5)
深度学习入门之自动求导(Pytorch)
Leetcode刷题---189
Leetcode skimming ---10