Convolutional neural network (CNN) learning notes (own understanding + own code) - deep learning

Abstract ： The content of the article is that I am learning Deep Learning Understanding in the process , The code is also typed by yourself （ Code ability is not very strong ）. If there is something wrong , Welcome to point out , correct .

Why use convolutional neural networks

There are two problems when using a fully connected network to process pictures

1. Too many parameters （ Hollow — The first hidden layer ; Solid — Input layer ）：

If the input picture is （100x100x3）, Then every neuron in the hidden layer to the input layer 30000 Two independent connections , Each connection corresponds to a weight parameter （weight）. With the increase of network size , The number of parameters will also rise sharply . This will make the training efficiency of the whole network very low , And it's easy to over fit .

2. Locally invariant features ： Convolutional neural networks have biological properties Feel the field Mechanism , It can better ensure the local invariance of the image .

at present CNN It is generally composed of convolution （Convolution）、 Pooling layer 【 Some books are also called convergence layer 】（Pooling）、 Fully connected layer （Linear） Cross stacked Feedforward neural networks . The full connection layer is generally CNN Top of .

CNN It has three structural characteristics ： Local invariance 、 Weight sharing 、 Converge . These characteristics make CNN It has a certain degree of local invariance , And there are fewer parameters than full connection .

Convolution （Convolution）

One dimensional convolution

Convolution in neural networks is actually well understood , Here's the picture ：（ The following formula can be expressed in matrix form in two-dimensional processing ）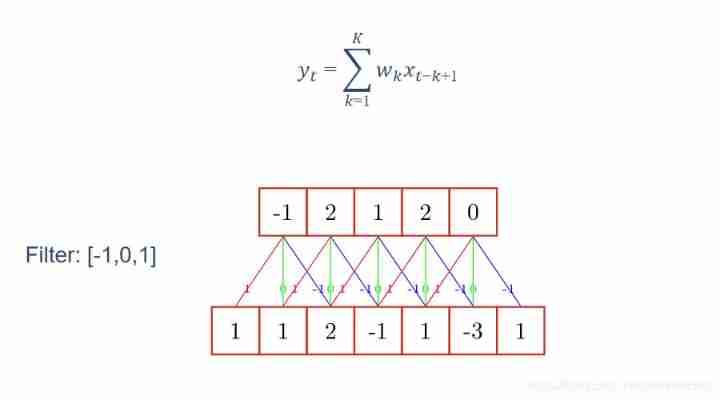

there Filter In signal processing, it is called filter , stay CNN Chinese is what we often use Convolution kernel . The value of convolution kernel [-1,0,1] Is the weight matrix . Given an input sequence （ The next row ） And a convolution kernel , After convolution , You can get an output sequence （ The upper row ）.

Different output sequences can be obtained by convoluting input sequences with different convolution kernels , That is to extract different features of the input sequence .

Two dimensional convolution

Because the image is a two-dimensional structure （ Has rows and columns ）, So we need to expand convolution （ The following figure shows the two-dimensional convolution operation ）：

You can add an offset after the above formula Bias;
Convolution kernel and bias are both learnable parameters .

In machine learning and image processing , The main function of convolution is to slide a convolution kernel on an image , A new set of features is obtained by convolution . Here's the picture ：

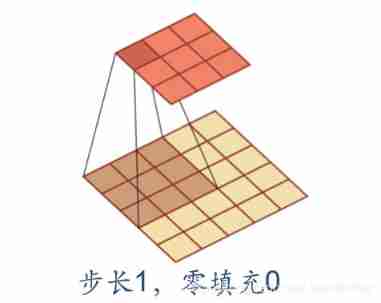
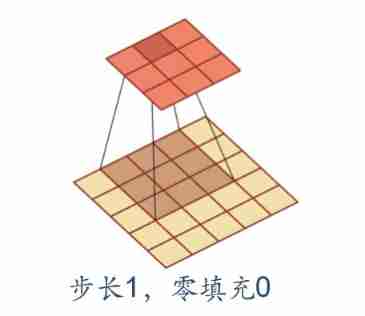
Step size and fill （Stride & padding）

In convolution , We can also introduce convolution kernel Sliding step and Zero fill To increase the diversity of convolution kernels , Feature extraction can be more flexible .

• step ： The time interval of convolution kernel in sliding （ Figuratively speaking, it is the span when sliding ）
• Zero fill ： Fill zero at both ends of the input vector

Here's the picture ：

Convolutional neural networks

According to the definition of convolution , Convolution layer has two very important properties ：

1. Local connection
2. Weight sharing

Convolutional neural network is to use convolution layer instead of full connection layer ：

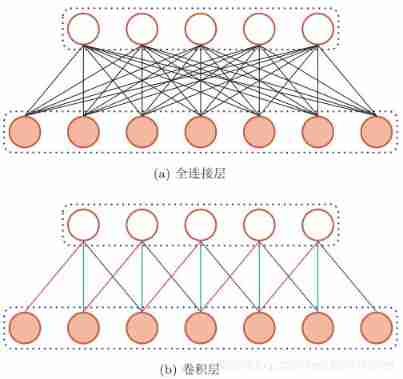
You can see , Because of the convolution layer Local connection Characteristics of , The convolution layer contains much less parameters than the full connection layer .

Weight sharing It can be understood that a convolution kernel only captures a specific local feature in the input data . therefore , If you want to extract multiple features, you need to use multiple different convolution kernels （ You can see clearly in the three-dimensional way behind ）. Pictured above , The weight of all connections with the same color is the same .

Because of local connectivity and weight sharing , The convolution layer has only one parameter K The weight of dimensions W^(l) And one-dimensional offset b^(l) , common K+1 Parameters .

Convolution layer

The function of convolution layer is to extract the features of a local region , Different convolution kernels are equivalent to different feature extractors .

Because the image is a two-dimensional structure , Therefore, in order to make full use of the local information of the image , Neurons are usually organized into three-dimensional neural layers , Size is height M x Width N x depth D, from D individual M x N The feature mapping of size constitutes .

Feature mapping is the feature extracted by convolution of an image , Each feature map can be used as a class of extracted image features .

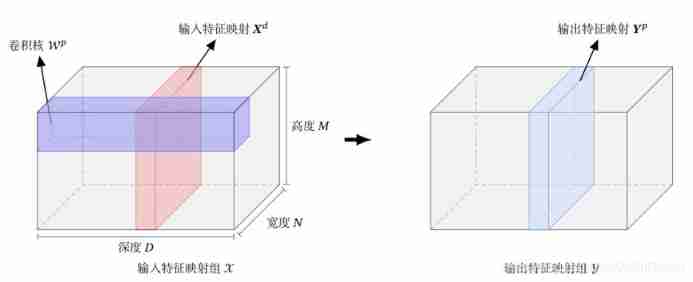
Such as a RGB picture , The depth in the above figure D Is the number of channels in the picture , Height and width correspond to the size of the picture . There are three convolution kernels corresponding to the output of three feature maps Y^p .

The calculation of feature mapping is shown in the figure below ：

Pooling layer （ Convergence layer ）

Although the convolution layer can significantly reduce the number of connections in the network , However, the number of neurons in the feature mapping group did not decrease significantly . If followed by a classifier , Its input dimension is still very high , It's easy to get over fitted . Thus, a pool layer is proposed .

The pooling layer is also called sub sampling layer , The function is to select features , Reduce the number of features , So that we can reduce the number of parameters .

Common pooling methods include ：

1. Maximum pooling （Max pooling）： Select the maximum activity value of all neurons in a region as the representation of this region .
2. The average pooling （Mean pooling）： Take the average value of neuron activity in the region as the representation of this region .

The maximum pooling is shown in the figure below ：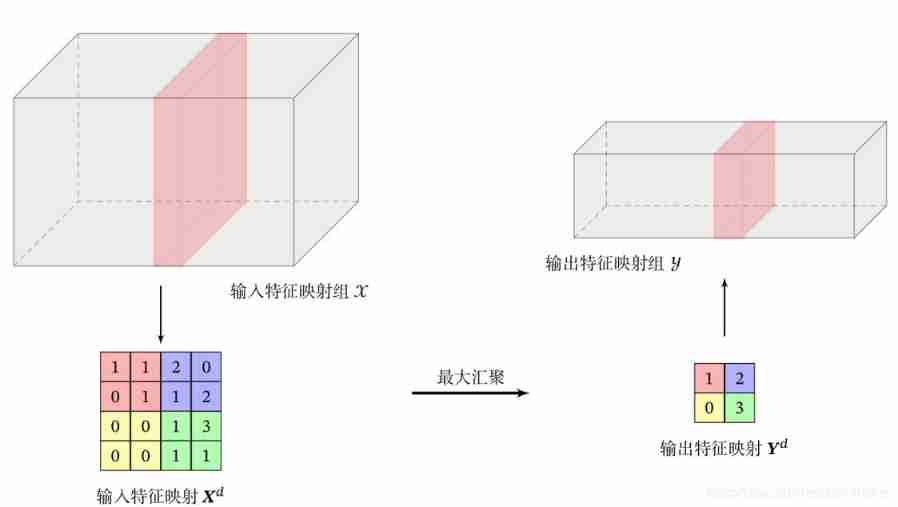

The overall structure of convolution network

The overall structure of the convolution network commonly used at present is shown in the figure below ：

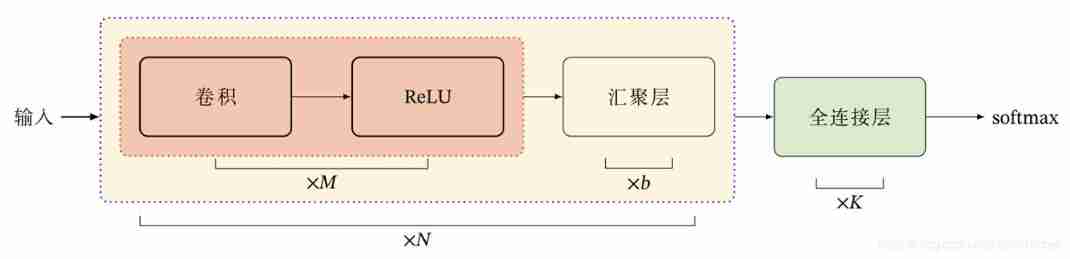
at present , The overall structure of convolution networks tends to use smaller convolution kernels （ The size of convolution kernel is generally odd ） And deeper network structure .

Besides , As the operability of the convolution layer becomes more and more flexible , The role of the pool layer is also getting smaller , Therefore, the current popular convolutional networks tend to be full convolutional Networks .

Residual network （Residual Net)

The residual network increases the propagation efficiency of information by adding direct edges to the nonlinear convolution layer .

• Suppose in a deep network , We expect a nonlinear element （ It can be one or more convolution layers ）f(x, y) To approximate an objective function h(x).
• Split the objective function into two parts ： Identity function and residual function

Residual unit ：

Residual network is a very deep network composed of many residual units in series .

Other convolution methods

Transposition convolution —— Low dimensional features are mapped to high dimensions ：

Cavity convolution —— By inserting... Into the convolution kernel “ empty ” To increase its size in disguise ：

Add

（1） We can go through ：

• Increase the size of the convolution kernel
• Increase the number of layers
• The convergence operation is performed before convolution

To increase the receptive field of the output unit

Code

Environmental preparation ：

• numpy
• anaconda
• Pycharm

One dimensional convolution

def Convolution_1d(input, kernel, padding=False, stride=1):

    input = np.array(input)
    kernel = np.array(kernel)
    kernel_size = kernel.shape[0]
    output = np.zeros((len(input) - kernel_size) // stride + 1)

    if padding:
        paddings = 1
        input_shape = len(input) + 2*paddings
        output = np.zeros((input_shape - kernel_size) // stride + 1)

    for i in range(len(output)):
        output[i] = np.dot(input[i:i+kernel_size], kernel)

    return output

Input ：

input = [2,5,9,6,3,5,7,8,5,4,5,2,5,6,3,5,8,7,1,0,5,0,10,20,60]
print('input_len: ', len(input))
kernel = [1,-1,1]
print('kernel_len: ', len(kernel))
output = Convolution_1d(input=input, kernel=kernel)
print('output_len: ', len(output))
print('output: ',output)

Output results ：

Two dimensional convolution

def Convolution_2d(input, kernel, padding=False, stride=1):

    input = np.array(input)
    kernel = np.array(kernel)
    stride = stride
    input_row = input.shape[0]
    input_col = input.shape[1]
    kernel_size = kernel.shape[0]
    output_row = (input_row - kernel_size) // stride + 1
    output_col = (input_col - kernel_size) // stride + 1
    output = np.zeros((output_row, output_col))

    if padding:
        padding=1
        input_row = input.shape[0]+2*padding
        input_col = input.shape[1]+2*padding
        output_row = (input_row-kernel_size) // stride + 1
        output_col = (input_col-kernel_size) // stride + 1
        output = np.zeros((output_row, output_col))

    for i in range(output_row):
        for j in range(output_col):
            output[i,j] = np.sum(input[i:i+kernel_size,j:j+kernel_size] * kernel)

    return output

Input ：

input = np.array([[2,7,3],[2,5,4],[9,4,2]])
kernel = np.array([[-1,1],[1,-1]])
output = Convolution_2d(input,kernel)
print('\n',output)

Output results ：

Two dimensional convolution can also be realized by one-dimensional convolution , Just make some modifications to the one-dimensional convolution .
High dimensional convolution can be achieved by modifying two-dimensional convolution .

The code is a little fragmented , Forgive me , Forgive me