Chromatic judgement bipartite graph

One 、 What is a bipartite graph ( Bipartite graph )？

Definition ： Bipartite graphs are also called bipartite graphs , It's a special model in graph theory . set up G=(V,E) It's an undirected graph , If the vertex V It can be divided into two disjoint subsets (A,B), And every edge in the graph （i,j） The two vertices associated i and j They belong to these two different vertex sets (i in A,j in B), It's called a picture G For a bipartite graph .
In other words ： All points of a graph can be divided into two disjoint subsets , And the two points attached to each edge in the graph belong to these two disjoint subsets , The vertices in two subsets are not adjacent .
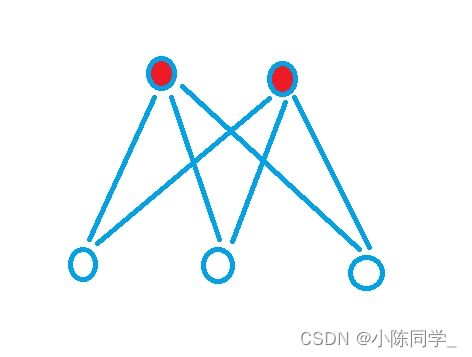
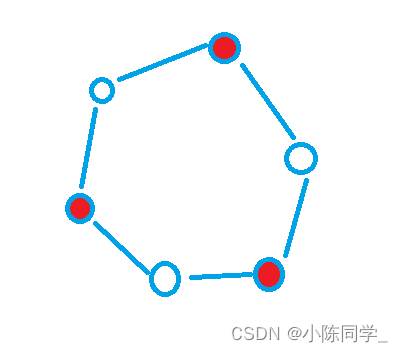
The following three graphs are bipartite graphs ：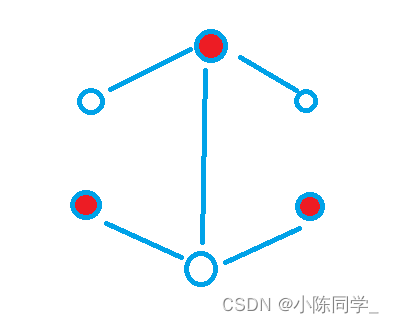

Two 、 How can we distinguish a bipartite graph ？

By definition , Distinguishing a bipartite graph is whether all points in the graph can be divided into two independent point sets .
To prove it , If a graph is a bipartite graph , Then there must not be an odd loop in the graph .
Because if there is a circuit in a graph and the length of this circuit is odd , Then the points in this circuit should also be odd . According to the previous definition , The two points attached to each edge belong to these two disjoint subsets , However, the number of points is odd , Therefore, it must not be divided into two disjoint subsets .
For example, the following figure is not a bipartite graph , We can find whether the dots in the box are white or red , Will make two points attached to an edge in a subset （ Same color ）.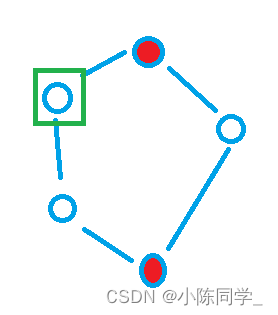

Here we use the coloring method to judge the bipartite graph （ Depth first search version ）

subject

Given a n A little bit m Undirected graph of strip and edge , There may be double edges and self rings in the graph .

Please judge whether this graph is bipartite .

Input format
The first line contains two integers n and m.

Next m That's ok , Each line contains two integers u and v, Indication point u Sum point v There is an edge between .

Output format
If a given graph is a bipartite graph , The output Yes, Otherwise output No.

Data range
1≤n,m≤10^5
sample input ：
4 4
1 3
1 4
2 3
2 4
sample output ：
Yes

---

This is a very basic introductory question , The title is to give us a picture , Let's judge whether it is a bipartite graph .

Ideas ：

1. Dyeing can use 1 and 2 Distinguish between different colors , use 0 Indicates not stained .
2. Traverse all points , Each time, the undyed points are searched for depth first , Default dyeing 1 perhaps 2
3. Here, if we cannot judge whether a certain point is dyed successfully, it means that the graph is a bipartite graph , To judge whether a certain point fails to stain ; Coloring failure is not a bipartite graph , Otherwise, it is a bipartite graph .

AC Code

#include <cstdio>
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;

const int N=1e5+10,M=2*1e5+10;  // Undirected graph , Number of edges *2

int h[N],e[M],ne[M],idx;
int color[N];
int n,m;

void add(int a,int b){
       // Adjacency list 
    e[idx]=b;
    ne[idx]=h[a];
    h[a]=idx++;
}

bool dfs(int u,int c){
    
    color[u]=c;
    for(int i=h[u];i!=-1;i=ne[i]){
    
        int j=e[i];
        if(!color[j]){
    
            if(!dfs(j,3-c)) return false;  // If at present j Nodes are not stained , Will judge j Will there be contradictions when nodes are dyed with another color , In case of contradiction, return false( Is not a bipartite graph )
        }
        else if(color[j]==c) return false;  // If the adjacent nodes have the same color , It's not a bipartite graph 
    }
    return true;   // If there is no dyeing failure, it will succeed 
}

int main(){
    
    int a,b;
    memset(h,-1,sizeof h);
    scanf("%d%d",&n,&m);
    while(m--){
    
        scanf("%d%d",&a,&b);
        add(a,b);   // Undirected graph 
        add(b,a);
    }
    bool flag=true;
    for(int i=1;i<=n;i++){
    
        if(!color[i]){
    
            if(!dfs(i,1)){
    
                flag=false;
                break;
            }
        }
    }
    if(flag)puts("Yes");
    else puts("No");
    return 0;
}