Verilog 和VHDL有符号数和无符号数相关运算

目录

一、Verilog有无符号数运算

1.有符号数和有符号数的加减运算（输入和输出为原码）

2.无符号数和有符号数的加减运算（输入和输出为原码）

3.有符号数和有符号数的乘法（输入和输出为原码）

二、VHDL深度讲解二进制无符号和有符号加法处理溢出的问题

1.Unsigned adders

2.Signed adders

2.1 Analysis

2.2 Summary

---

一、Verilog有无符号数运算

1.有符号数和有符号数的加减运算（输入和输出为原码）

step1：将数据转换为补码。

step2：确定输出结果的位宽。
（结果的位宽是在最大的一个数据的位宽基础上加一位。如6bit与3bit进行加减，则结果为7bit。)

step3：扩展符号位到输出结果的位宽，然后直接进行运算。

step4：处理输出结果。（因为得到的结果是补码，需要转化为原码后再输出。转换方法：判断符号位，如果符号位为0，表明是一个正数，则直接输出（正数原码和补码相等）。如果符号位是1，表明是一个负数，需要符号位不变，有效位取反加一后再输出（补码变原码）。)

例1：（-3） -（-6）
分析：-3用有符号数表示，原码为3bit的111。-6用有符号数表示，原码为4bit的1110。

step1：将每一个数都转换成补码。-3的补码为101，-6的补码为1010

step2：确定输出结果的位宽。最大的一个数据的位宽是4bit,则输出结果的位宽为5bit的有符号数。

step3：扩展符号位到输出结果的位宽，然后直接进行运算。
输出结果out=1_1101-1_1010=0_0011(注意结果要取5bit)

step4：符号位out[5] = 0,表明为正数数，则直接输出，out=0_0011(+3)

例2：（-3） - （+6）
分析：-3用有符号数表示，原码为3bit的111。+6用有符号数表示，原码为4bit的0110。

step1：转换成补码。-3的补码为101，+6的补码为0110。（正数的补码与原码相同）

step2：确定输出结果的位宽。最大的一个数据的位宽是4bit,则输出结果的位宽为5bit的有符号数。

step3：扩展符号位到输出结果的位宽，然后直接进行运算。
输出结果out=1_1101-0_0110=1_0111(注意结果要取5bit)

step4：符号位out[5] = 1,表明为负数，则符号位不变，有效为取反加一后输出，out=1_1001(-9)

2.无符号数和有符号数的加减运算（输入和输出为原码）

step1：将无符号数转换为有符号数。

step2：将数据转换为补码。

step3：确定输出结果的位宽。
（结果的位宽是在最大的一个数据的位宽基础上加一位。如6bit与3bit进行加减，则结果为7bit。)

step4：扩展符号位到输出结果的位宽，然后直接进行运算。

step5：处理输出结果。（因为得到的结果是补码，需要转化为原码后再输出。转换方法：判断符号位，如果符号位为0，表明是一个正数，则直接输出（正数原码和补码相等）。如果符号位是1，表明是一个负数，需要符号位不变，有效位取反加一后再输出（补码变原码）。)

例3： （3） + （-6）

分析：3用无符号数表示，原码为2bit的11。-6用有符号数表示，原码为4bit的1110。
step1：将无符号数转换为有符号数。2bit的无符号数11，为有符号数3bit的011

step2：转换成补码。3的补码为011，-6的补码为1010。（正数的补码与原码相同）

step3：确定输出结果的位宽。最大的一个数据的位宽是4bit,则输出结果的位宽为5bit的有符号数。

sep4：扩展符号位到输出结果的位宽，然后直接进行运算。
输出结果out=0_0011+1_1010=1_1101(注意结果要取5bit)

step5：符号位out[5] = 1,表明为负数，则符号位不变，有效为取反加一后输出，out=1_0011(-3)

总结：无符号数和有符号数的计算可转变为有符号数和有符号数的计算。

3.有符号数和有符号数的乘法（输入和输出为原码）

step1：确定输出结果位宽。（一个符号位+两个数据有效为的位宽之和，如1个4bit的有符号数A,和1个5bit的有符号数B相乘，A的有效位是3bit,B的有效位为4bit,则输出结果的有效位宽为7bit,总位宽为8bit）。

step2：计算输出结果的符号位。（两个数据的符号位进行异或，判断是正数还是负数）。

step3：计算输出结果的有效位。（直接将两个数据相乘，得到的结果就是输出结果的有效位）。

step4：将符号位和有效位拼接后输出。

例4：（-3）*（-6）

分析：-3用有符号数表示，原码为3bit的111。-6用有符号数表示，原码为4bit的1110。

step1：确定输出结果位宽。（-3的有效位是2bit,-6的有效位为3bit,则输出结果的有效位宽为5bit,总位宽为6bit）。

step2：计算输出结果的符号位。两个数据的符号位都是1，则1^1=0，则输出结果是正数。

step3：计算输出结果的有效位。2'b11 * 3'b110 = 5'b1_0010。

step4：将符号位和有效位拼接后输出。out=6'b01_0010(+18)

ps:如果输入是补码，则运算之前先转换为原码，在按照以上步骤即可。

二、VHDL深度讲解二进制无符号和有符号加法处理溢出的问题

1.Unsigned adders

这个比较简单，只需在A、B前面扩展一位0防止溢出，溢出的数填到第n位cout，n-1到0位就是sum。

2.Signed adders

一开始也搞不懂下图中为什么要扩展符号位，两个符号位了怎么加？   往下看↓

2.1 Analysis

在真正开始使用Verilog做signed加法运算前，我们先来看看实际上二进制singed加法是如何运算?

Normal Condition (没有Overflow)

(+6) + (-3) = (+3)

为了节省resource，我们故意使用4 bit的+6与3 bit的-3相加，若直接将两个signed值相加，答案为-7，很显然答案并不正确。

因为4 bit与3 bit相加，结果可能进位到5 bit，正确的作法是将4 bit的+6做signed extension到5 bit，且3 bit的-3也要做signed extension到5 bit后，然后才相加，若最后进位到6 bit，则不考虑6 bit的值。

在此补充一下何谓Singed Extension?简单的说，当以较多bit显示signed型态的值时，重复signed bit补齐。

就意义上来说，就是3 bit的signed值若要以5 bit表示时，必须补上signed bit才能在5 bit表示，所以101要变成11101。

Boundary Condition (正Overflow)

 (+7) + (+3) = (+10)

为了节省resource，我们一样故意使用4 bit的+7与3 bit的+3相加，若直接将两个signed值相加，答案为-6，很显然答案并不正确。

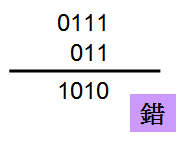
根据上个例子的经验，+7与+3必须做signed extension才能相加，这样才能得到正确答案+10。

不过现在问题来了，+10必须动到5 bit才能显示，若输出的值域为4 bit，只能-8 ~ +7，+10很显然已经正overflow了‧

若只能以4 bit表示，因为是正的，MSB必须是0(SUM[3]=0)，所以若MSB是1就表示由进位而来，也就是正overflow了(此例的SUM[3]为1，所以已经正overflow)，再加上因为目前运算结果为5 bit，且是正，所以SUM[5]必须为0。

也就是说，若SUM[5]=0且SUM[4]=1时，为正overflow，所以01010对于4 bit来说，是正overflow。

Boundary Condition (负Overflow)

(-5) + (-4) = (-9)

同样为了节省resource，我们故意使用4 bit的-5与3 bit的-4相加，若直接将两个signed值相加，答案为-1，很显然的答案并不正确。

根据前面两个例子，-5与-4一样必须做signed extension才能相加，这样才能得到正确答案-9‧进位到6 bit的1要舍去，所以答案是10111‧

问题一样来了，-9必须动到5 bit才能显示，若输出的值域是4 bit，只能-8 ~ +7，-9很显然已经是负overflow了。

若只能以4 bit表示，因为是负的，MSB必须是1(SUM[3]=1)，所以若MSB是0就表示由进位而来，也就是负overflow了(此例的SUM[3]为0，所以已经负overflow)，再加上因为目前运算结果为5 bit，且是负，所以SUM[5]必须为1‧

也就是说，若SUM[5]为1且SUM[4]为0时，为负overflow，所以10111对于4 bit来说，是负overflow。

2.2 Summary

根据之前三个实际的例子，我们得到以下结论：

m bit + m bit =< (m+1) bit m bit + n bit =< (m+1) bit，其中n < m ul style='list-style:disc outside none;' > m bit与n bit都必须先做signed extension到(m+1) bit才能相加 若结果有到(m+2) bit则忽略之，实际的结果为(m+1) bit 若Sum[m+1] ^ Sum[m]为1，表示有overflow 若Sum[m+1]为0且Sum[m]为1，则为正overflow 若Sum[m+1]为1且Sum[m]为0，则为负overflow

[1]如何实现有符号无符号加减法，如何处理overflowhttp://www.eeskill.com/article/id/4575

参考链接：verilog中有符号数和无符号数的相关运算_海畔风的博客-CSDN博客_verilog有符号数和无符号数运算

【VHDL】深度讲解二进制无符号和有符号加法处理溢出的问题