当前位置:网站首页>2022 The 4th C.Easy Counting Problem (EGF+NTT)
2022 The 4th C.Easy Counting Problem (EGF+NTT)
2022-08-05 05:11:00 【The wonderful sauce of eating peppercorns】
题意:give a charset,大小不超过10,第icharacters appear no less than ci,求字符串长度为n的方案数,至多300个询问,ci<=5000,n<=1e7
(Pictures are not copied,I don't know if the competition for money will be held==)
思路:指数生成函数
由egf定义,第k个字符的egf为 f ( k ) = ∑ c k + o o x i i ! f(k)=\sum_{c_k}^{+oo}\frac{x^i}{i!} f(k)=∑ck+ooi!xi
则答案为 [ x n n ! ] ∏ k = 1 w f ( k ) , w 为字符集大小 [\frac{x^n}{n!}]\prod_{k=1}^w{f(k)},w为字符集大小 [n!xn]∏k=1wf(k),w为字符集大小
但是n比较大,It's definitely not possible to roll directly.改写一下f(k)的形式
f ( k ) = e x p ( x ) − ∑ i = 0 c k − 1 x i i ! f(k)=exp(x)-\sum_{i=0}^{c_k-1}\frac{x^i}{i!} f(k)=exp(x)−∑i=0ck−1i!xi
可以将exp(x)看成一个整体,The final answer is in the form
∑ i = 0 w g ( i ) ∗ e x p ( x ) i = ∑ i = 0 w g ( i ) ∗ e x p ( i x ) , 其中 g ( i ) 是一个多项式 \sum_{i=0}^wg(i)*exp(x)^i=\sum_{i=0}^wg(i)*exp(ix),其中g(i)是一个多项式 ∑i=0wg(i)∗exp(x)i=∑i=0wg(i)∗exp(ix),其中g(i)是一个多项式
g(i)The maximum number of times does not exceed ∑ c i \sum{c_i} ∑ci,而exp(ix)Each coefficient of is known,Then just loop over eachg(i)The coefficient of the term is multiplied byexp(ix)Corresponding coefficients are sufficient.最后别忘了乘n!
The specific spelling can be used for referencedp的思路,设dpij表示前i个fThe formula obtained by multiplyingexp(jx)What is the coefficient of ,There is a polynomial
转移方程 d p i , j = d p i − 1 , j − d p i , j − 1 ∗ ∑ k = 0 c i − 1 x k k ! dp_{i,j}=dp_{i-1,j} - dp_{i,j-1}*\sum_{k=0}^{c_i-1}\frac{x^k}{k!} dpi,j=dpi−1,j−dpi,j−1∗∑k=0ci−1k!xk,In fact, it is just a simulation of polynomial violence,This way of thinking a little clearer.
复杂度 O ( w 2 s l o g s + q w s ) , s = ∑ c i O(w^2slogs+qws),s=\sum{ci} O(w2slogs+qws),s=∑ci
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define IOS ios::sync_with_stdio(false),cin.tie(nullptr)
#define _for(i,a,b) for(int i=(a) ;i<=(b) ;i++)
#define _rep(i,a,b) for(int i=(a) ;i>=(b) ;i--)
#define mst(v,s) memset(v,s,sizeof(v))
#define pii pair<int ,int >
#define pb(v) push_back(v)
#define all(v) v.begin(),v.end()
#define int long long
#define inf 0x3f3f3f3f
#define INF 0x7f7f7f7f7f7f7f7f
#define endl "\n"
#define fi first
#define se second
#define ls p<<1
#define rs p<<1|1
#define lson p<<1,l,mid
#define rson p<<1|1,mid+1,r
#define AC return 0
#define ldb long double
const int maxn = 6e6+10;
const int p = 998244353;
const int mod = 998244353;
int Pow(int x,int d){
int tans = 1;
if(d == 0)return 1%p;
int a = Pow(x,d/2);
tans = 1ll*a*a%p;
if(d%2)tans = 1ll*tans*x%p;
return tans%p;
}
typedef vector<int> Poly;//多项式定义
inline Poly operator + (const Poly&A ,const Poly&B){
Poly res (max(A.size(),B.size()),0);
for(int i=0 ;i<max(A.size(),B.size()) ;i++){
if( i < A.size() && i<B.size() ) res[i] = (A[i]+B[i])%mod;
else if( i >= A.size() ){
res[i] = B[i];
}
else res[i] = A[i];
}
return res;
}
inline Poly operator - (const Poly&A ,const Poly&B){
Poly res (max(A.size(),B.size()),0);
for(int i=0 ;i<max(A.size(),B.size()) ;i++){
if( i < A.size() && i<B.size() ) res[i] = (A[i]-B[i]+mod)%mod;
else if( i >= A.size() ){
res[i] = (mod-B[i])%mod;
}
else res[i] = A[i];
}
return res;
}
int F1[maxn],F2[maxn];
int rev[maxn];
void NTT(int * A,int lim,int opt) {
int i, j, k, m, gn, g, tmp;
for(int i = 0; i < lim; ++i)rev[i] = (i & 1)*(lim >> 1) + (rev[i >> 1] >> 1);
for(i = 0; i < lim; ++i)if (rev[i] < i) swap(A[i], A[rev[i]]);
for(m = 2; m <= lim; m <<= 1) {
k = m >> 1;
gn = Pow(3,(p - 1) / m);
for(i = 0; i < lim; i += m) {
g = 1;
for (j = 0; j < k; ++j, g = 1ll * g * gn % p) {
tmp = 1ll * A[i + j + k] * g % p;
A[i + j + k] = (A[i + j] - tmp + p) % p;
A[i + j] = (A[i + j] + tmp) % p;
}
}
}
if(opt == -1){
reverse(A+1,A+lim);
int inv = Pow(lim,p-2);
for(i = 0; i < lim; ++i) A[i] = 1ll * A[i] * inv % p;
}
}
Poly mul(const Poly & A,const Poly & B){
int n = A.size(),m = B.size();
int siz = n + m - 1;
Poly C(siz);
if(siz < 64){
//小于等于64项直接暴力算
for(int i = 0;i < n;i++){
for(int j = 0;j < m;j++)C[i+j] = (C[i+j] + 1LL*A[i]*B[j]%p)%p;
}
return C;
}
int fsiz = 1;
while(fsiz <= siz)fsiz *= 2;
for(int i = 0;i < fsiz;i++)F1[i] = F2[i] = 0;
for(int i = 0;i < n;i++)F1[i] = A[i];
for(int i = 0;i < m;i++)F2[i] = B[i];
NTT(F1,fsiz,1);
NTT(F2,fsiz,1);
for(int i = 0;i < fsiz;i++)F1[i] = 1ll*F1[i]*F2[i]%p;
NTT(F1,fsiz,-1);
for(int i = 0;i < siz;i++){
C[i] = F1[i];
}
return C;
}
const int N = 5e5+10;
const int M = 1e7+5;
int W,n;
int c[11],fac[M],ni_f[M];
int mi[11][M];
Poly f[11][11];
ll qsm(int a,int b){
a %= mod;
ll ans=1,tmp=a;
while( b ){
if( b&1 ) ans = (ans * tmp)%mod;
tmp = tmp * tmp%mod;
b>>=1;
}
return ans;
}
void ini(){
int mx = 1e7;
fac[0]=1;
_for(i,1,mx) fac[i] = fac[i-1]*i%mod;
ni_f[mx] = qsm(fac[mx],mod-2);
_rep(i,mx-1,0) ni_f[i] = ni_f[i+1]*(i+1)%mod;
}
int S;
void ff(Poly F){
F.resize(min(S+1,(int)F.size()));
}
void solve(){
f[1][1].resize(1,1);
f[1][0].resize(c[1]+1,0);
_for(i,0,c[1]-1){
f[1][0][i] = (mod-ni_f[i])%mod;
}
_for(i,2,W){
_for(j,0,i){
Poly t (c[i]+1,0);
_for(k,0,c[i]-1){
t[k] = (mod-ni_f[k])%mod;
}
f[i][0] = mul(f[i-1][0],t);
ff(f[i][0]);
f[i][j] = (f[i-1][j-1] + mul(f[i-1][j],t));
ff(f[i][j]);
}
}
}
int Q(int n){
int ans=0;
for(int i=0 ;i<=W ;i++){
// exp(ix)
int pw = qsm(i,n-min(n,(int)f[W][i].size()-1ll));
for(int j=min(n,(int)f[W][i].size()-1ll) ;j>=0 ;j--){
int t = n-j;
if( j < min(n,(int)f[W][i].size()-1ll) ) pw = pw * i%mod;
ans = (ans + f[W][i][j] * pw %mod*ni_f[t]%mod)%mod;
}
}
return ans*fac[n]%mod;
}
signed main(){
#ifndef ONLINE_JUDGE
freopen("in.txt", "r", stdin);
#endif
IOS;
cin>>W;
_for(i,1,W) cin>>c[i];
S = accumulate(c+1,c+1+W,0ll);
ini();
solve();
int q;cin>>q;
while( q-- ){
int x;cin>>x;
int ans = Q(x);
cout<<ans<<endl;
}
AC;
}
边栏推荐
- 1068 Find More Coins
- Dashboard Display | DataEase Look at China: Data Presents China's Capital Market
- 判断语句_switch与case
- 2023 International Conference on Information and Communication Engineering (JCICE 2023)
- software management rpm
- 人性的弱点
- How to identify false evidence and evidence?
- human weakness
- C#关于set()和get()方法的理解及使用
- The underlying mechanism of the class
猜你喜欢
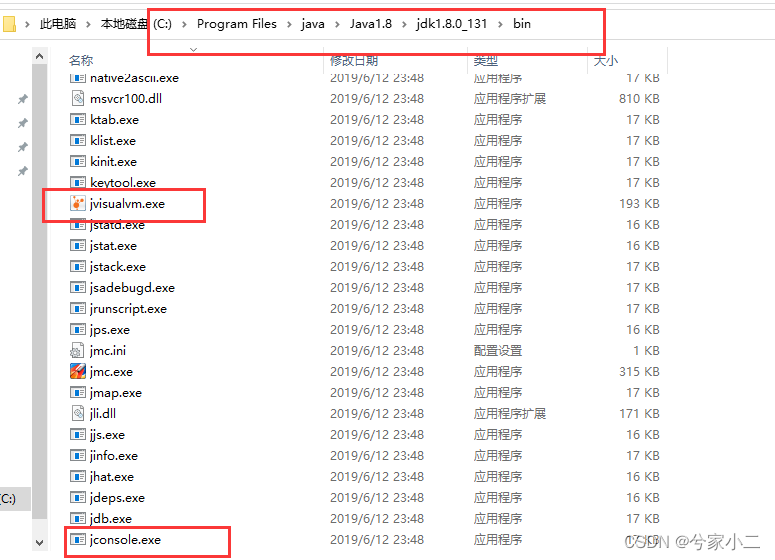
jvm 三 之堆与栈

Structured light 3D reconstruction (1) Striped structured light 3D reconstruction
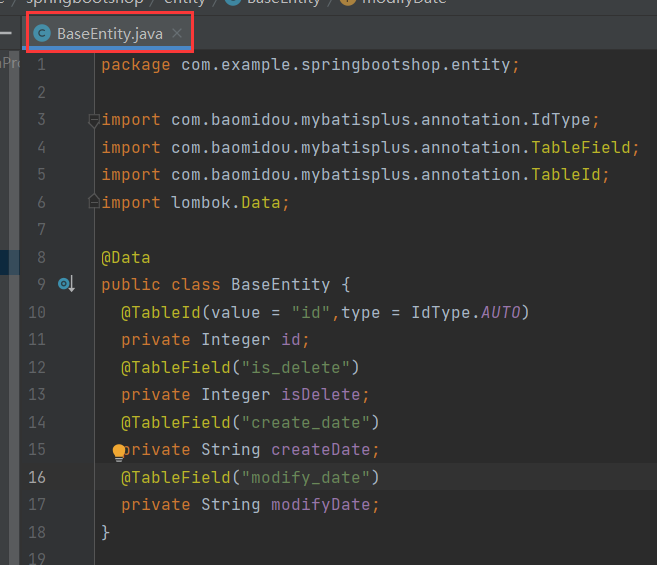
8.04 Day35-----MVC three-tier architecture

What is ASEMI photovoltaic diode, the role of photovoltaic diode

基于Web的商城后台管理系统的设计与实现
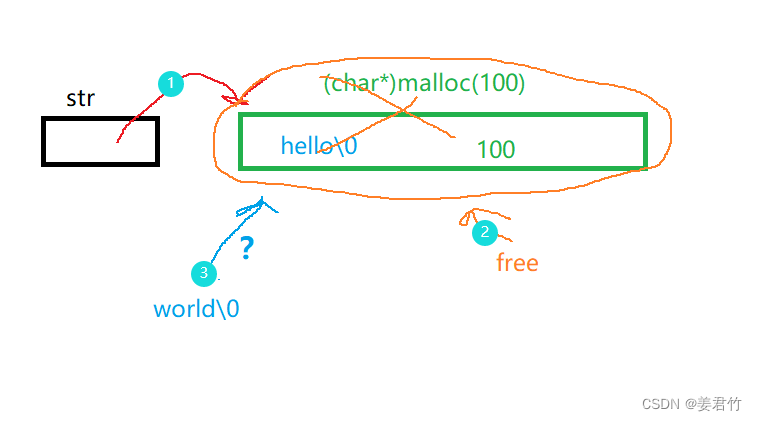
【学习笔记之菜Dog学C】动态内存管理之经典笔试题
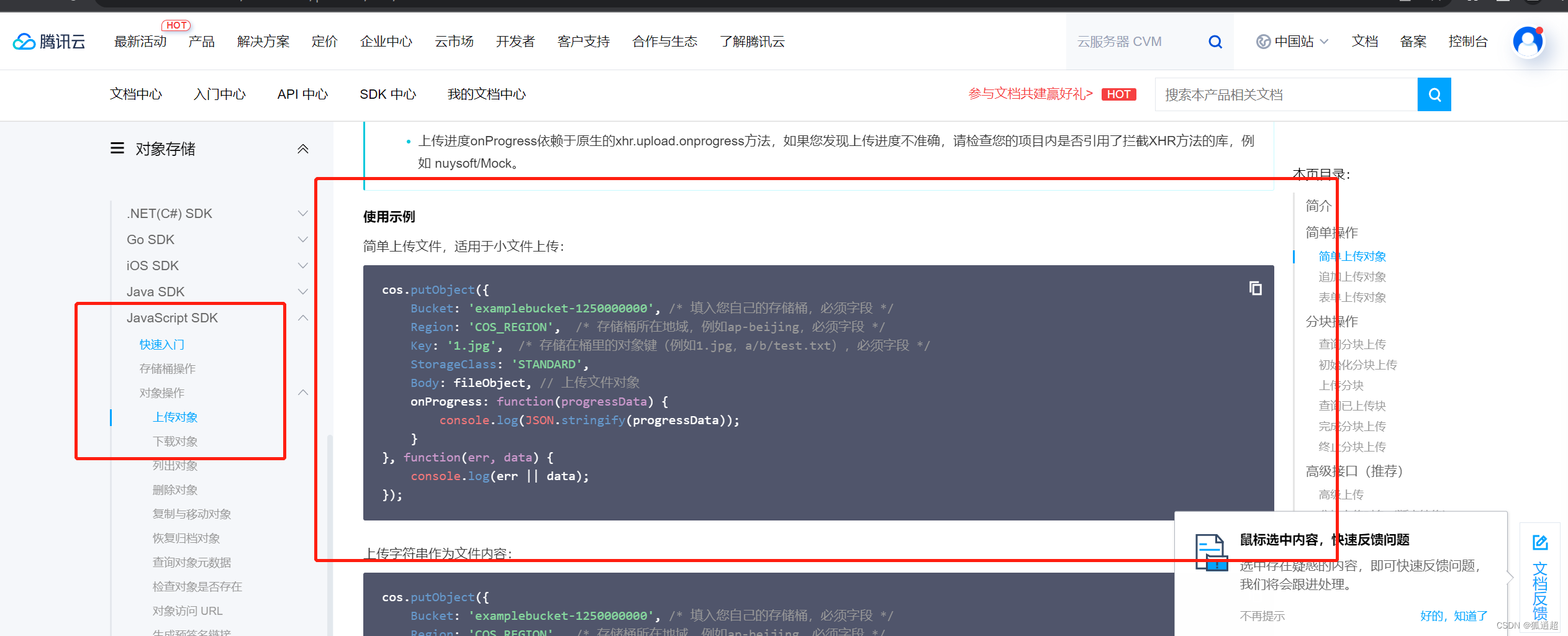
upload upload pictures to Tencent cloud, how to upload pictures
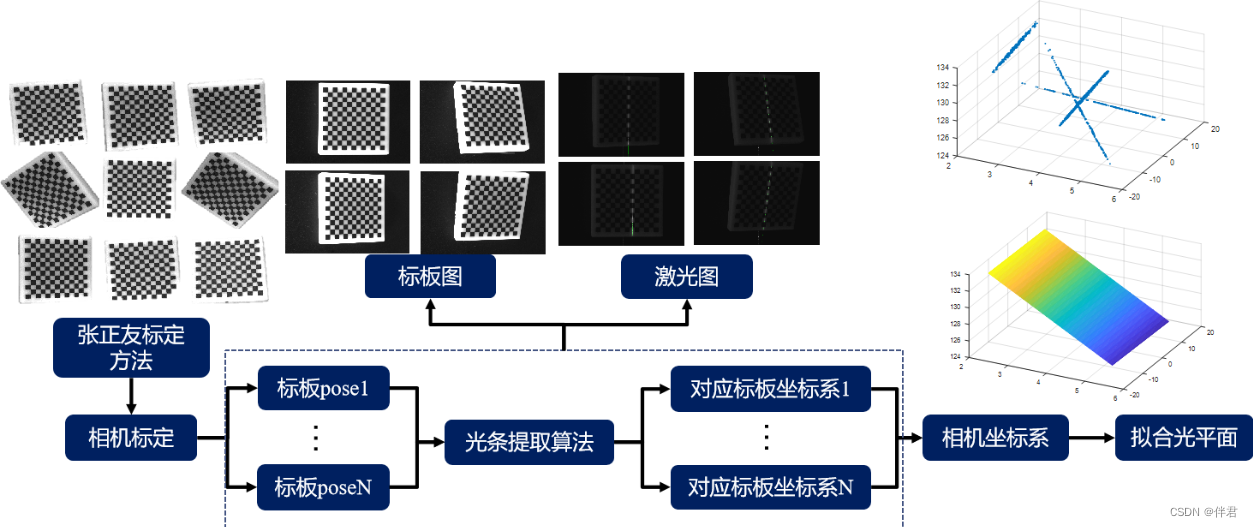
Structured Light 3D Reconstruction (2) Line Structured Light 3D Reconstruction
![[cesium] element highlighting](/img/99/504ca9802db83eb33bc6d91b34fa84.png)
[cesium] element highlighting

算法---一和零(Kotlin)
随机推荐
ansible各个模块详解
2023 International Conference on Information and Communication Engineering (JCICE 2023)
jvm 三 之堆与栈
Day019 方法重写与相关类的介绍
mutillidae download and installation
1068找到更多的硬币
In the hot summer, teach you to use Xiaomi smart home accessories + Raspberry Pi 4 to connect to Apple HomeKit
C#关于set()和get()方法的理解及使用
Talk about 20 common problems in data governance
数字孪生技术在电力系统中的应用现状
LAB Semaphore Implementation Details
u-boot调试定位手段
MySQL Foundation (1) - Basic Cognition and Operation
数字_获取指定位数的小数
请写出SparkSQL语句
How does the Flutter TapGestureRecognizer work
【cesium】Load and locate 3D Tileset
Homework 8.4 Interprocess Communication Pipes and Signals
Excel画图
2022杭电多校第一场01