Stack
The stack is OI A linear data structure commonly used in .
The stack is modified according to the principle of last in first out , So stack is usually called last in first out (last in first out) surface , abbreviation LIFO surface .
The following uses the name st , The bottom of the stack is st[1] , The top of the stack is st[top] Array simulation stack .
The advantage of this is , It is easy to operate :
| operation | Code |
|---|---|
| Size of query stack | top |
| Check if the stack is empty | top |
| Query the top elements of the stack | st[top] |
| Insert elements \(x\) | st[++top] = x; |
| Pop up top element | top--; |
Monotonic stack
What is monotonous stack
seeing the name of a thing one thinks of its function , Monotone stack is a stack structure that satisfies monotonicity . Compared with monotonic queues , It only goes in and out at one end .
Strictly ?
Strict inequality : It only contains marks \(>\) or \(<\) The inequality of is called strict inequality .
Non strict inequality : Contain marks \(\leq\) or \(\geq\) The inequality of is called non strict inequality .
therefore 「 Strictly greater than 」 Namely \(>\),「 Strictly less than 」 Namely \(<\).
Strictly monotonically increasing ( reduce ), It refers to everything except the first element , Each element is strictly greater than ( Less than ) The former element .
application
Consider such a question : Given a sequence of Numbers , For each number , Before finding this number, the first number that is strictly greater than it .
Suppose the number sequence is :\([81, 45, 11, 0, 14, 26]\), Insert the elements into the stack in turn .
Pictured 1-1, At this time, the front \(4\) Elements , The next element to be inserted is \(14\).
chart 1-1( Figure since OI-Wiki)
In order to find \(14\) The first element larger than it , Maintain monotony , Will compare \(14\) Small elements pop up , Then it pops up \(0\) and \(11\)
Pictured 1-2, At this point in the stack \(14\) The previous element of is \(45\), therefore \(14\) The first element larger than it was \(45\).
chart 1-2( Figure since OI-Wiki)
Suppose the next inserted element is \(x\).
If \(14 \leq x\), So then \(14\) Definitely not ( Elements \(x\) Of ) answer , So \(14\) It's still small \(0, 11\) It is even less likely to be the answer .
If \(14 > x\), that \(14\) That's the answer. , Don't think about \(0, 11\).
therefore ,\(0, 11\) Will no longer contribute to the following answers ( influence ), It can pop up .
The idea of dealing with problems with monotony is Eliminate impossible options in time , Keep the strategy highly effective and orderly , So as to provide more conditions and possible methods for us to make decisions .
Code implementation
#include<iostream>
#include<cstdio>
using namespace std;
int main(){
int n = 6;
int a[6] = {81, 45, 11, 0, 14, 26}, ans[6] = { };
int st[6] = { }, top = 0;
for(int i = 0; i < n; i++){
while(top && st[top] <= a[i]){ // Pay attention to top Determine whether the stack is empty , It can only be judged if it is not empty
printf("pop %d.\n", st[top]);
top--;
}
if(top){
ans[i] = st[top];
}else{
ans[i] = -1; // There is nothing bigger than this number , It outputs -1
}
printf("push %d.\n", a[i]);
st[++top] = a[i];
printf("stack: ");
for(int j = 1; j <= top; j++){
printf("%d ", st[j]);
}
puts("\n");
}
printf("ans: ");
for(int i = 0; i < n; i++){
printf("%d ", ans[i]);
}
return 0;
}
Running results :
push 81.
stack: 81
push 45.
stack: 81 45
push 11.
stack: 81 45 11
push 0.
stack: 81 45 11 0
pop 0.
pop 11.
push 14.
stack: 81 45 14
pop 14.
push 26.
stack: 81 45 26
ans: -1 81 45 11 45 45
Complexity of time and space
The spatial complexity is obviously \(O(n)\).
Look at the core of the code :
// ……
for(int i = 0; i < n; i++){
while(top && st[top] <= a[i]){
printf("pop %d.\n", st[top]);
top--;
}
// ……
}
// ……
Pay attention to the inner layer while loop , It is used to pop up elements with the top of the stack smaller than the element to be inserted .
Each element is only pushed once , It will only come out of the stack once , So the inner layer while In total, the loop will only execute \(n\) Time , The time complexity of the whole monotone stack code is \(O(n)\).
Monotone stack simple application
Monotone stack template problem
Topic link
Lougu P5788 【 Templates 】 Monotonic stack
Topic summary
Given a length of \(N\) Sequence of numbers , For each number , After finding this number, the first element that is strictly larger than it The subscript .
analysis
It is found that the monotonous stack cannot be processed , Consider doing the opposite .
At this point, you need to maintain a Strictly monotonic decreasing The stack , That is, pop up all elements smaller than it at the top of the stack before inserting elements .
If the stack is empty before inserting , The answer is \(0\), Otherwise, it is the top element .
One thing to pay attention to in this question is , What is required is the element Subscript , So the stack should store subscripts , Not data .
The subscript used for the title is \(1 \sim n\), For convenience, the subscript of the program is also used \(1 \sim n\).
Reference code
#include<iostream>
#include<cstdio>
using namespace std;
const int N = 3e6 + 10;
int n, a[N], ans[N];
int st[N], top;
int main(){
scanf("%d", &n);
for(int i = 1; i <= n; i++){
scanf("%d", &a[i]);
}
for(int i = n; i > 0; i--){
while(top && a[st[top]] <= a[i]){
top--;
}
if(top){
ans[i] = st[top];
}else{
ans[i] = 0;
}
st[++top] = i;
}
for(int i = 1; i <= n; i++){
printf("%d ", ans[i]);
}
return 0;
}
Bad Hair Day
Topic link
Luogu P2866 [USACO06NOV]Bad Hair Day S
Topic summary
Yes \(N (N \leq 80,000)\) First milk steak in a line , Each cow has a height \(h_{i}\), Ask each cow to see the sum of the hair of how many cows ahead .
analysis
cow A Saw the cow B Hair of , It's equivalent to cows B The hair of the cow A I saw it .
It is difficult to ask how many cows' hair each cow can see behind , But you can ask how many cows in front of you can see the hair of each cow , The final and of these two solutions are the same .
So the problem is transformed into 「 How many cows in front can see the hair of each cow 」.
Using the monotone stack , Maintain a Strictly monotonic decreasing The stack .
Reference code
#include<iostream>
#include<cstdio>
using namespace std;
const int N = 8e4 + 10;
int n, x;
int st[N], top;
long long ans;
int main(){
scanf("%d", &n);
for(int i = 0; i < n; i++){
scanf("%d", &x);
while(top && st[top] <= x){
top--;
}
ans += top;
st[++top] = x;
}
printf("%lld\n", ans);
return 0;
}
Monotonic stack offline processing RMQ problem
「 Templates 」ST surface
It's actually RMQ The template questions .
Topic link
Luogu P3865 【 Templates 】ST surface
Topic summary
Given \(n\) Sum of numbers \(m\) Group inquiry , Each group of questions has a range \(l, r\), Find the maximum value of this interval .
What is the RMQ
RMQ It's English Range Maximum(Minimum) Query Abbreviation , It means that the query range is the largest ( Minimum ) value .
Common algorithms :
| Algorithm | Whether online | Preprocessing time complexity | The time complexity of a single inquiry | Total time complexity | Spatial complexity |
|---|---|---|---|---|---|
| ST surface | On-line | \(O(n \log n)\) | \(O(1)\) | \(O(n \log n + n) \approx O(n \log n)\) | \(O(n \log n)\) |
| Line segment tree | On-line | \(O(n)\) | \(O(log n)\) | \(O(n + m \log n) \approx O(m \log n)\) | \(O(n)\) |
| …… | …… | …… | …… | …… | …… |
| Monotonic stack | offline | \(O(m \log m)\) | \(O(\log n)\) | \(O(m \log m + m \log n) \approx O(m \log m)\) | \(O(n)\) |
among \(n\) Is the size of the array ,\(m\) Is the number of queries .
You can go to RMQ - OI Wiki see .
Online and offline
If an algorithm can answer every query instantly , The algorithm is called On-line Of , Otherwise it is called offline Of .
analysis
Read in all queries , Then sort by the right end of the query from small to large .
Process elements in turn , Maintain strictly monotonically decreasing stacks .
If it reaches the right end of a query , Then binary monotone stack , Find the first subscript at the bottom of the stack that is larger than this query \(l\) The elements of , Record answer .
See code Notes for details .
Reference code
#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
const int N = 1e5 + 10, M = 2e6 + 10;
struct qt{
int id, l, r;
}q[M]; // Structure storage query
int n, a[N], m;
int st[N], top;
int ans[M];
bool cmp(qt x, qt y){
return x.r < y.r;
} // Sort by right endpoint from small to large
int main(){
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; i++){
scanf("%d", &a[i]);
}
for(int i = 0; i < m; i++){
q[i].id = i;
scanf("%d%d", &q[i].l, &q[i].r);
}
sort(q, q+m, cmp);
int nw = 0; // Currently processed queries
for(int i = 1; i <= n && nw < m; i++){ // Process each element in turn , Insert into the stack , Maintain strictly monotonically decreasing stacks
while(top && a[st[top]] <= a[i]){
top--;
}
st[++top] = i;
while(i == q[nw].r){ // If the current processing reaches the right endpoint of a query ( Because the right endpoint may repeat , So use while Instead of if)
int l = 1, r = top; // The first subscript in the dichotomy stack is larger than that of this query l The elements of
while(l < r){
int mid = (l + r) / 2;
if(st[mid] >= q[nw].l){
r = mid;
}else{
l = mid + 1;
}
}
ans[q[nw].id] = a[st[l]]; // Record answer
nw++; // Deal with the next problem
}
}
for(int i = 0; i < m; i++){
printf("%d\n", ans[i]);
}
return 0;
}
summary
Maintain a stack , Make the stored data monotonous , Such a stack is called a monotone stack .
Monotone stack is used to solve 「 The element in the sequence is left / The first one on the right is bigger than it / Small elements 」.
Because each element can go in and out of the stack at most once , So the time complexity is \(O(n)\).
Monotone stacks are often combined with other algorithms , Common examples are dichotomy .
practice
Largest Rectangle in a Histogram
Topic link
POJ 2559 Largest Rectangle in a Histogram
AcWing 131. The largest rectangle in the histogram
Topic summary
Given \(n\) The height of a column , Find the area of the largest rectangle in the polygon .
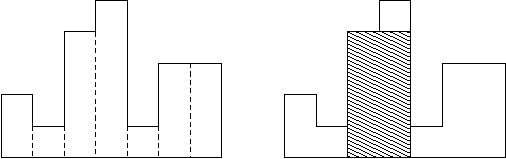
analysis
Observation found that , The largest rectangle must be a column high .
Enumerate each column , Find the first column shorter than it on the left , And the first shorter column on the right , You can calculate the area of the largest rectangle with this column as the height , Finally, take the maximum of all the answers .
「 Find the first column shorter than it on the left , And the first shorter column on the right 」 It can be processed with monotonic stack .
Reference code
#include<iostream>
#include<cstdio>
using namespace std;
const int N = 1e5 + 10;
int n;
int h[N], l[N], r[N];
int st[N], top;
long long ans;
int main(){
while(scanf("%d", &n), n != 0){
ans = 0;
for(int i = 1; i <= n; i++){
scanf("%d", &h[i]);
}
// Deal with the first shorter column on the left
top = 0;
for(int i = 1; i <= n; i++){
while(top && h[st[top]] >= h[i]){
top--;
}
// if(top){
// l[i] = st[top];
// }else{
// l[i] = 0;
// }
// If top == 0,st[top] == st[0] == 0, So it can also be written like this :
l[i] = st[top];
st[++top] = i;
}
// Deal with the first column shorter than it
top = 0;
for(int i = n; i > 0; i--){
while(top && h[st[top]] >= h[i]){
top--;
}
if(top){
r[i] = st[top];
}else{
r[i] = n+1;
}
st[++top] = i;
}
for(int i = 1; i <= n; i++){
ans = max(ans, (long long)(r[i]-l[i]-1)*h[i]);
} // Calculate the maximum area of the rectangle with each column as the height
printf("%lld\n", ans);
}
return 0;
}







![[Tera term] black cat takes you to learn TTL script -- serial port automation skill in embedded development](/img/63/dc729d3f483fd6088cfa7b6fb45ccb.png)
