当前位置:网站首页>Campus network problems
Campus network problems
2022-07-04 06:47:00 【chengqiuming】
One Link to original question
Network of Schools - POJ 1236 - Virtual Judge https://vjudge.net/problem/POJ-1236
https://vjudge.net/problem/POJ-1236
Two Output and output
1 Input
The first 1 Line inclusion 1 It's an integer N, Indicates the number of online secondary schools . The school starts from the front N A positive integer identifies . Next N That's ok , Each line describes the recipient list , The first i+1 Line contains school i The identifier of the recipient of the . Each list is marked with 0 ending . The empty list contains only 0.
2 Output
The output contains two lines . The first 1 The row should contain subtasks 1 Solution , The first 2 The row should contain subtasks 2 Solution .
3、 ... and Input and output examples
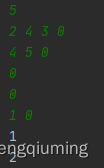
1 sample input
5
2 4 3 0
4 5 0
0
0
1 0
2 sample output
1
2
Four Ideas
1 The subtasks 1
At least to how many schools , So that the software can reach all schools ? actually , After finding the strongly connected components and shrinking points , Each entry is 0 All strongly connected components of must receive a new copy of the software .
sample input 1, The composition diagram is as follows , It includes 3 Strong connected components , The depth after shrinking point is 0 The strongly connected components of are 1 individual , At least send to 1 One school is enough , namely 1、2、5 Any school in .
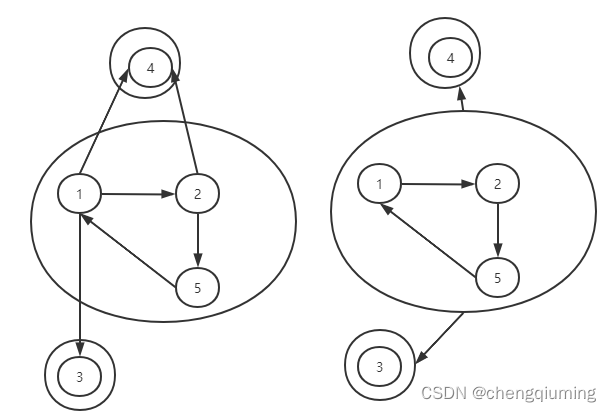
2 The subtasks 2
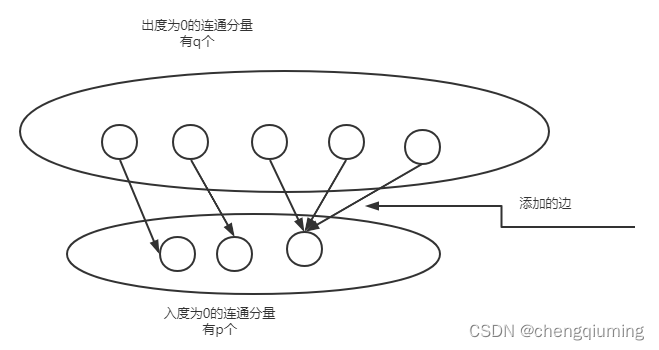
At least how many receiving relationships are added , Can be sent to any school , All schools can receive ? in other words , Every strongly connected component must have an in degree , Again . The penetration is 0 The strong connected component of ,, Add at least one degree ; For an exit of 0 The strong connected component of , Add at least one exit . The number of edges added is max(p,q), As shown in the figure below .
A special case : If there is only one strongly connected component , At least 1 A school , The number of edges to add is 0.
5、 ... and Algorithm design
1 use Targan The algorithm solves strongly connected components , Mark the connected component number .
2 Check each node u Every adjacent point of v, If the connected component numbers are different , be u The outgoing degree of the connected component number is 1,v The degree of connected component sign is 1.
3 The statistical penetration is 0 Number of connected components p And the output is 0 The connected component of q, seek max(p,q).
6、 ... and Code
package graph.poj1236;
import java.util.Scanner;
import java.util.Stack;
public class POJ1236 {
static final int maxn = 1000 + 5;
static int n;
static int head[];
static int belong[];
static int cnt;
static int low[];
static int dfn[];
static int out[]; // Out degree of node
static int in[]; // The penetration of nodes
static int num;
static int id;
static boolean ins[];
static Stack<Integer> s = new Stack<>();
static Edge e[] = new Edge[maxn << 1];
static {
for (int i = 0; i < e.length; i++) {
e[i] = new Edge();
}
}
static void add(int u, int v) { // Add an edge u--v
e[++cnt].to = v;
e[cnt].next = head[u];
head[u] = cnt;
}
/**
* Function description :tarjan Algorithm
*
* @param u Start node
* @author cakin
* @date 2022/7/3
*/
static void tarjan(int u) { // Solving the strongly connected components of a digraph
low[u] = dfn[u] = ++num;
ins[u] = true;
s.push(u);
for (int i = head[u]; i != 0; i = e[i].next) {
int v = e[i].to;
if (dfn[v] == 0) {
tarjan(v);
low[u] = Math.min(low[u], low[v]);
} else if (ins[v])
low[u] = Math.min(low[u], dfn[v]);
}
if (low[u] == dfn[u]) {
int v;
id++;
do {
v = s.peek();
s.pop();
belong[v] = id;
ins[v] = false;
} while (v != u);
}
}
static void init() {
head = new int[maxn];
low = new int[maxn];
dfn = new int[maxn];
out = new int[maxn];
in = new int[maxn];
belong = new int[maxn];
ins = new boolean[maxn];
cnt = num = 0;
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
n = scanner.nextInt();
init();
for (int i = 1; i <= n; i++) {
int v;
while (true) {
v = scanner.nextInt();
if (v == 0) {
break;
}
add(i, v);
}
}
for (int i = 1; i <= n; i++)
if (dfn[i] == 0)
tarjan(i);
for (int u = 1; u <= n; u++)
for (int i = head[u]; i != 0; i = e[i].next) {
int v = e[i].to;
if (belong[u] != belong[v]) {
in[belong[v]]++;
out[belong[u]]++;
}
}
if (id == 1) {
System.out.println(1);
System.out.println(0);
return;
}
int ans1 = 0, ans2 = 0;
for (int i = 1; i <= id; i++) {
if (in[i] == 0)
ans1++;
if (out[i] == 0)
ans2++;
}
System.out.println(ans1);
System.out.println(Math.max(ans1, ans2));
}
}
class Edge {
int to;
int next;
}7、 ... and test
Green is the output , White is the output .
边栏推荐
- Shopping malls, storerooms, flat display, user-defined maps can also be played like this!
- P26-P34 third_ template
- Wechat applet scroll view component scrollable view area
- C语言中的排序,实现从小到大的数字排序法
- 请问旧版的的常用SQL怎么迁移到新版本里来?
- 2022年6月小结
- leetcode 310. Minimum Height Trees
- thread priority
- Tree DP
- Code rant: from hard coding to configurable, rule engine, low code DSL complexity clock
猜你喜欢

2022 where to find enterprise e-mail and which is the security of enterprise e-mail system?
Can the out of sequence message complete TCP three handshakes
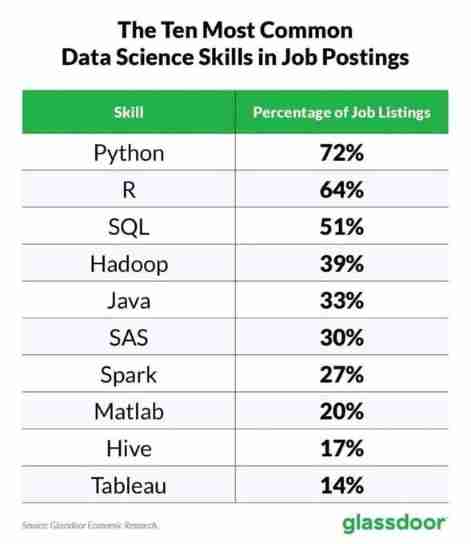
List of top ten professional skills required for data science work
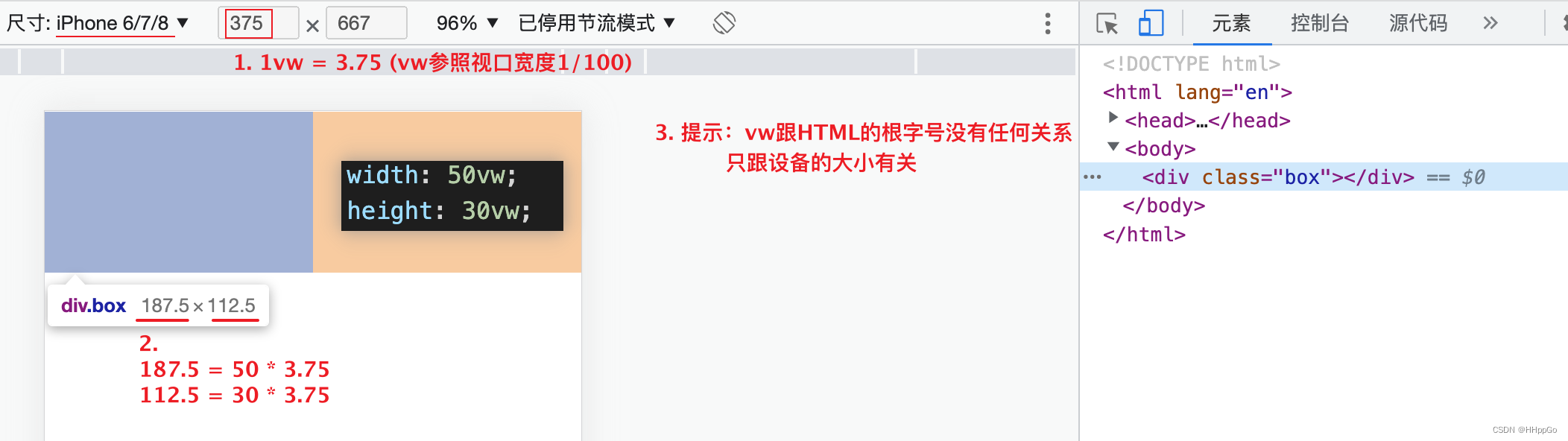
移动适配:vw/vh
![[number theory] fast power (Euler power)](/img/1e/5d032c8f2e43f553b4543d28ea2a2d.jpg)
[number theory] fast power (Euler power)

centos8安装mysql.7 无法开机启动

Bicolor case
![[GF (q) + LDPC] regular LDPC coding and decoding design and MATLAB simulation based on the GF (q) field of binary graph](/img/5e/7ce21dd544aacf23b4ceef1ec547fd.png)
[GF (q) + LDPC] regular LDPC coding and decoding design and MATLAB simulation based on the GF (q) field of binary graph
Native Cloud - SSH articles must be read on Cloud (used for Remote Login to Cloud Server)
Variables d'environnement personnalisées uniapp
随机推荐
The sorting in C language realizes the number sorting method from small to large
uniapp小程序分包
Highly paid programmers & interview questions: how does redis of series 119 realize distributed locks?
Boast about Devops
7. Agency mode
leetcode 310. Minimum Height Trees
Uniapp custom environment variables
运算符<< >>傻瓜式测试用例
JS common time processing functions
SQL injection SQL lab 11~22
MySQL 45 lecture learning notes (XIV) count (*)
图的底部问题
Another company raised the price of SAIC Roewe new energy products from March 1
8. Factory method
2022 where to find enterprise e-mail and which is the security of enterprise e-mail system?
thread priority
How does the recv of TCP socket receive messages of specified length?
selenium IDE插件下载安装使用教程
Tar source code analysis Part 10
1、 Relevant theories and tools of network security penetration testing