当前位置:网站首页>【Day1】 deep-learning-basics
【Day1】 deep-learning-basics
2022-07-04 09:37:00 【weixin_45965693】
ps:我还是觉得csdn比博客园好用。记在这里吧。
get!New
1. yield关键字
1.含有yield的函数称为【生成器函数】,调用【生成器函数】返回的结果称为【生成器】
2.【生成器】对象实际上就是【迭代器】,那么肯定满足【迭代器协议】:
__iter__返回迭代器对象自身__next__每次返回一个迭代数据,如果没有数据,则要抛出StopIteration异常
它的运行方式和迭代器是一致的:
- 通过
next()函数调用 - 每次
next()都会在遇到yield后返回结果 - 如果函数运行结束(即遇到
return)则抛出StopIteration异常
4.yield关键字最根本的作用是改变了函数的性质,返回对象,和类差不多
5.yield语句(Python2.2):Simple Generators
6.yield表达式(Python2.5):Coroutines【协程】 via Enhanced Generators
# 本函数已保存在d2lzh包中方便以后使用
def data_iter(batch_size, features, labels):
num_examples = len(features)
indices = list(range(num_examples))
random.shuffle(indices) # 样本的读取顺序是随机的
for i in range(0, num_examples, batch_size):
j = nd.array(indices[i: min(i + batch_size, num_examples)])
yield features.take(j), labels.take(j) # take函数根据索引返回对应元素
batch_size = 10
for X, y in data_iter(batch_size, features, labels):
print(X, y)
break # 比较随机得遍历一遍就好了
2. 使用autograd自动求导
from mxnet import autograd
x.attach_grad()申请存储梯度所需要的内存。
例如:函数 y = 2 x ⊤ x y = 2\boldsymbol{x}^{\top}\boldsymbol{x} y=2x⊤x 关于 x \boldsymbol{x} x 的梯度应为 4 x 4\boldsymbol{x} 4x
首先,需要调用autograd.record()要求MXNet记录与求梯度有关的计算。
(可以对【控制流(如条件和循环控制)】求梯度)
with autograd.record():
y = 2 * nd.dot(x.T, x)
然后,y.backward()自动求梯度
线性回归linear-regression
scratch
from mxnet import autograd, nd
import random
训练集 X ∈ R 1000 × 2 \boldsymbol{X} \in \mathbb{R}^{1000 \times 2} X∈R1000×2
样本1000,特征个数2
标签 y = X w + b + ϵ \boldsymbol{y} = \boldsymbol{X}\boldsymbol{w} + b + \epsilon y=Xw+b+ϵ
线性回归模型真实权重 w = [ 2 , − 3.4 ] ⊤ \boldsymbol{w} = [2, -3.4]^\top w=[2,−3.4]⊤
偏差 b = 4.2 b = 4.2 b=4.2
随机噪声项 ϵ \epsilon ϵ(噪声项 ϵ \epsilon ϵ服从均值为0、标准差为0.01的正态分布)
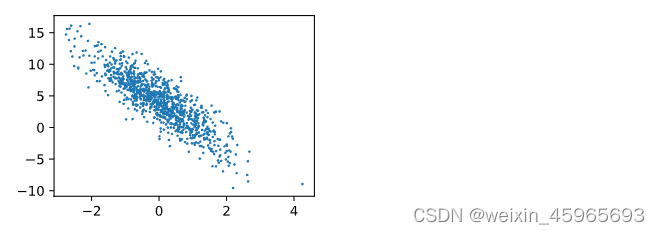
x:features y:labels
初始化【模型参数】:权重初始化成均值为0、标准差为0.01的正态随机数,偏差则初始化成0
定义【损失函数】:平方损失
定义【优化算法】:小批量随机梯度下降算法
训练模型:每次迭代中,我们根据当前读取的小批量数据样本(特征X和标签y),通过调用反向函数backward计算小批量随机梯度并调用【优化算法】sgd迭代【模型参数】来优化【损失函数】。
#初始化模型参数
w = nd.random.normal(scale=0.01, shape=(num_inputs, 1))
b = nd.zeros(shape=(1,))
params = [w, b]
for param in params:
param.attach_grad()
#定义模型
def net(X):
return nd.dot(X, w) + b
#损失函数
def squared_loss(y_hat, y): # 本函数已保存在d2lzh包中方便以后使用
return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2
#优化
def sgd(params, lr, batch_size): # 本函数已保存在d2lzh包中方便以后使用
for param in params:
param[:] = param - lr * param.grad / batch_size
lr = 0.03
num_epochs = 3
net = linreg
loss = squared_loss
for epoch in range(num_epochs): # 训练模型一共需要num_epochs个迭代周期
# 在每一个迭代周期中,会使用训练数据集中所有样本一次(假设样本数能够被批量大小整除)。X
# 和y分别是小批量样本的特征和标签
for X, y in data_iter(batch_size, features, labels):
with autograd.record():
l = loss(net(X, w, b), y) # l是有关小批量X和y的损失
l.backward() # 小批量的损失对模型参数求梯度
sgd([w, b], lr, batch_size) # 使用小批量随机梯度下降迭代模型参数
train_l = loss(net(features, w, b), labels)
print('epoch %d, loss %f' % (epoch + 1, train_l.mean().asnumpy()))
gluon
from mxnet.gluon import nn
net = nn.Sequential()
net.add(nn.Dense(1))
from mxnet import init
net.initialize(init.Normal(sigma=0.01))
from mxnet.gluon import loss as gloss
loss = gloss.L2Loss() # 平方损失又称L2范数损失
from mxnet import gluon
trainer = gluon.Trainer(net.collect_params(), 'sgd', {
'learning_rate': 0.03})
num_epochs = 3
for epoch in range(1, num_epochs + 1):
for X, y in data_iter:
with autograd.record():
l = loss(net(X), y)
l.backward()
trainer.step(batch_size)
l = loss(net(features), labels)
print('epoch %d, loss: %f' % (epoch, l.mean().asnumpy()))
多类逻辑回归softmax-regression
scratch
问题1. exp会导致数值稳定性变差
https://freemind.pluskid.org/machine-learning/softmax-vs-softmax-loss-numerical-stability/
def softmax(X):
X_exp = X.exp()# 变成正数
partition = X_exp.sum(axis=1, keepdims=True)# 对行求和
return X_exp / partition # 这里应用了广播机制
# 使得,每一行都是正和为1
def net(X):
return softmax(nd.dot(X.reshape((-1,num_inputs)), W) + b)
【交叉熵损失函数】:将两个概率分布的负交叉熵作为目标值
最小化这个值等价于最大化这两个概率的相似度
【计算精度】:预测概率最高的那个类作为预测的类,通过比较真实标号计算
def cross_entropy(yhat, y):
return - nd.pick(nd.log(yhat),y)
def accuracy(output, label):
return nd.mean(output.argmax(axis=1)==label).asscalar()
# 本函数已保存在d2lzh包中方便以后使用。该函数将被逐步改进:它的完整实现将在“图像增广”一节中
# 描述
def evaluate_accuracy(data_iter, net):
acc_sum, n = 0.0, 0
for X, y in data_iter:
y = y.astype('float32')
acc_sum += accuracy(net(X),y)
n += y.size
return acc_sum / n
训练+accuracy test_acc
num_epochs, lr = 5, 0.1
# 本函数已保存在d2lzh包中方便以后使用
def train_ch3(net, train_iter, test_iter, loss, num_epochs, batch_size,
params=None, lr=None, trainer=None):
for epoch in range(num_epochs):
train_l_sum, train_acc_sum, n = 0.0, 0.0, 0
for X, y in train_iter:
with autograd.record():
y_hat = net(X)
l = loss(y_hat, y).sum()
l.backward()
if trainer is None:
d2l.sgd(params, lr, batch_size)
else:
trainer.step(batch_size) # “softmax回归的简洁实现”一节将用到
y = y.astype('float32')
train_l_sum += l.asscalar()
train_acc_sum += (y_hat.argmax(axis=1) == y).sum().asscalar()
n += y.size
test_acc = evaluate_accuracy(test_iter, net)
print('epoch %d, loss %.4f, train acc %.3f, test acc %.3f'
% (epoch + 1, train_l_sum / n, train_acc_sum / n, test_acc))
train_ch3(net, train_iter, test_iter, cross_entropy, num_epochs, batch_size,
[W, b], lr)
gluon
net = nn.Sequential()
with net.name_scope():
net.add(gluon.nn.Flatten())# 输入
net.add(nn.Dense(10))# 输出
net.initialize(init.Normal(sigma=0.01))
# Softmax和交叉熵一起
softmax_cross_entropy = gluon.loss.SoftmaxCrossEntropyLoss()
# 使用学习率为0.1的小批量随机梯度下降作为优化算法
trainer = gluon.Trainer(net.collect_params(), 'sgd', {
'learning_rate': 0.1})
多层感知机
Scratch
激活函数:在层之间插入【非线性】的激活函数 r e l u ( x ) = m a x ( x , 0 ) relu(x)=max(x,0) relu(x)=max(x,0)(计算简单)
def relu(X):
return nd.maximum(X, 0)
def net(X):
X = X.reshape((-1, num_inputs))
H = relu(nd.dot(X, W1) + b1)
return nd.dot(H, W2) + b2
gluon
net = nn.Sequential()
with net.name_scope():
net.add(nn.Flatten())
net.add(nn.Dense(256, activation='relu'),nn.Dense(10))
# 多加几个隐含层
net.add(nn.Dense(256, activation='relu'),nn.Dense(10))
net.add(nn.Dense(10))
net.initialize(init.Normal(sigma=0.01))
欠拟合和过拟合underfit-overfit
欠拟合:训练误差就很大
过拟合:训练误差 泛化误差 相差过大
多项式拟合
y ^ = b + ∑ k = 1 K x k w k \hat{y}=b+\sum_{k=1}^{K}x^{k}w_{k} y^=b+k=1∑Kxkwk
目标:找一个K阶多项式,其由向量 w w w和位移 b b b组成,来最好地近似每个样本 x x x和 y y y,并以平方误差为损失函数。
特别地,一阶多项式拟合又叫线性拟合。
具体生成数据样本
y = 1.2 x − 3.4 x 2 + 5.6 x 3 + 5.0 + n o i s e y=1.2x-3.4x^{2}+5.6x^{3}+5.0+noise y=1.2x−3.4x2+5.6x3+5.0+noise
n_train, n_test, true_w, true_b = 100, 100, [1.2, -3.4, 5.6], 5
features = nd.random.normal(shape=(n_train + n_test, 1))
poly_features = nd.concat(features, nd.power(features, 2),
nd.power(features, 3))
labels = (true_w[0] * poly_features[:, 0] + true_w[1] * poly_features[:, 1]
+ true_w[2] * poly_features[:, 2] + true_b)
labels += nd.random.normal(scale=0.1, shape=labels.shape)
略
def fit_and_plot(train_features, test_features, train_labels, test_labels)
三阶多项式拟合
fit_and_plot(poly_features[:n_train, :], poly_features[n_train:, :],
labels[:n_train], labels[n_train:])
线性拟合
fit_and_plot(features[:n_train, :], features[n_train:, :], labels[:n_train],
labels[n_train:])
训练样本不足
fit_and_plot(poly_features[0:2, :], poly_features[n_train:, :], labels[0:2],
labels[n_train:])
正则化reg【罚】
引入 L 2 \bold{L}_{2} L2范数正则化
我们在训练时的最小化就变为:
l o s s + λ ∑ p ∈ p a r a m s ∣ ∣ p ∣ ∣ 2 2 loss+\lambda\sum_{p\in params}||p||_{2}^{2} loss+λp∈params∑∣∣p∣∣22
1.fit loss 2.权衡模型不要特别复杂。直观上, L 2 \bold{L}_{2} L2试图惩罚较大绝对值的参数值,使得 w w w和 b b b变小一点。
值得注意的是,在测试模型时, λ \lambda λ必须为0。
def net(X, lambd, w, b):
return nd.dot(X, w) + b + lambd * ((w**2).sum() + b**2)
用高维线性回归引入一个【过拟合】问题
使用如下的线性函数来生成数据样本
y = 0.05 + ∑ i = 1 p 0.01 x i + n o i s e y=0.05+\sum_{i=1}^{p}0.01x_{i}+noise y=0.05+i=1∑p0.01xi+noise
边栏推荐
- Summary of reasons for web side automation test failure
- Are there any principal guaranteed financial products in 2022?
- Write a jison parser from scratch (2/10): learn the correct posture of the parser generator parser generator
- Some summaries of the third anniversary of joining Ping An in China
- System. Currenttimemillis() and system Nanotime (), which is faster? Don't use it wrong!
- Write a jison parser from scratch (1/10):jison, not JSON
- Hands on deep learning (44) -- seq2seq principle and Implementation
- 自动化的优点有哪些?
- 用数据告诉你高考最难的省份是哪里!
- 百度研发三面惨遭滑铁卢:面试官一套组合拳让我当场懵逼
猜你喜欢
C语言指针经典面试题——第一弹

Servlet基本原理与常见API方法的应用

Hands on deep learning (33) -- style transfer
Svg image quoted from CodeChina

百度研发三面惨遭滑铁卢:面试官一套组合拳让我当场懵逼

Hands on deep learning (42) -- bi-directional recurrent neural network (BI RNN)
Summary of reasons for web side automation test failure
Latex download installation record
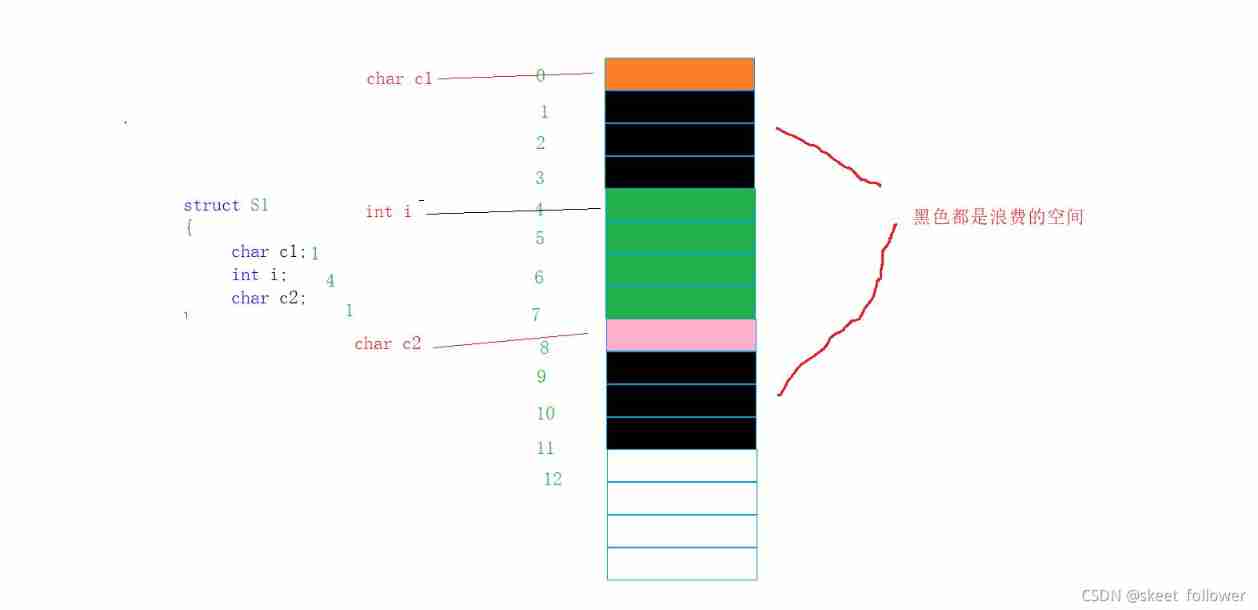
Custom type: structure, enumeration, union
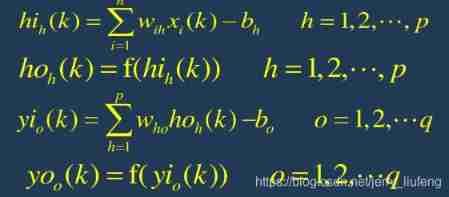
Machine learning -- neural network (IV): BP neural network
随机推荐
Log cannot be recorded after log4net is deployed to the server
Write a jison parser (7/10) from scratch: the iterative development process of the parser generator 'parser generator'
How do microservices aggregate API documents? This wave of show~
MySQL transaction mvcc principle
华为联机对战如何提升玩家匹配成功几率
Golang defer
Kotlin: collection use
Hands on deep learning (39) -- gating cycle unit Gru
Regular expression (I)
Luogu deep foundation part 1 Introduction to language Chapter 4 loop structure programming (2022.02.14)
Exercise 9-5 address book sorting (20 points)
libmysqlclient. so. 20: cannot open shared object file: No such file or directory
Hands on deep learning (35) -- text preprocessing (NLP)
System.currentTimeMillis() 和 System.nanoTime() 哪个更快?别用错了!
uniapp 处理过去时间对比现在时间的时间差 如刚刚、几分钟前,几小时前,几个月前
Daughter love in lunch box
法向量点云旋转
Kotlin:集合使用
Problems encountered by scan, scanf and scanln in golang
Golang Modules
