当前位置:网站首页>codeforces k-Tree (dp仍然不会耶)
codeforces k-Tree (dp仍然不会耶)
2022-08-02 14:23:00 【先求一个导】
题目
题意: 给定一棵树,每个节点恰好有k个儿子,对应的边恰好为1-k. 求一下有多少种方案,满足路径上的权值恰好为n,且至少有一个边满足边权>=d.
思路: 其实就是个线性dp,每一层只能选1-k.好久没dp就d不出来了,可以先dp一遍1-k都能用的,再dp一遍只能用1-(d-1)的,相减就是满足题意的.f[0][i][j]: 用全部边,从前i层中选,边权恰好为j的方案数。只需枚举当前这一层用多少权值,即可递推出。f[0][i][j] = f[0][i-1][j-1…k]
只依赖于上一层,所以可以把i这一维给压缩掉。f[0][j] = f[0][j-1…k]
时间复杂度: O(n* n * k)或O(n*k)
代码:
#include<bits/stdc++.h>
using namespace std;
const int N = 102;
const int mod = 1e9+7;
int n,m,k,T;
int f[2][N]; //0:所有边,1:小于d的边,f[j]:权值为j的方案数
void solve()
{
cin>>n>>k>>m;
f[0][0] = 1;
for(int j=1;j<=n;++j) //权值
{
for(int t=1;t<=k;++t) //枚举从哪转移
{
if(j-t<0) break;
f[0][j] = (f[0][j] + f[0][j-t]) % mod;
}
}
k = m-1;
f[1][0] = 1;
for(int j=1;j<=n;++j) //权值
{
for(int t=1;t<=k;++t) //枚举从哪转移
{
if(j-t<0) break;
f[1][j] = (f[1][j] + f[1][j-t]) % mod;
}
}
long long ans = 0;
ans = (ans + f[0][n]) % mod;
ans = (ans - f[1][n]) % mod;
ans = (ans + mod) % mod;
cout<<ans;
}
signed main(void)
{
solve();
return 0;
}
边栏推荐
猜你喜欢
【时间序列模型】AR模型(原理剖析+MATLAB代码)
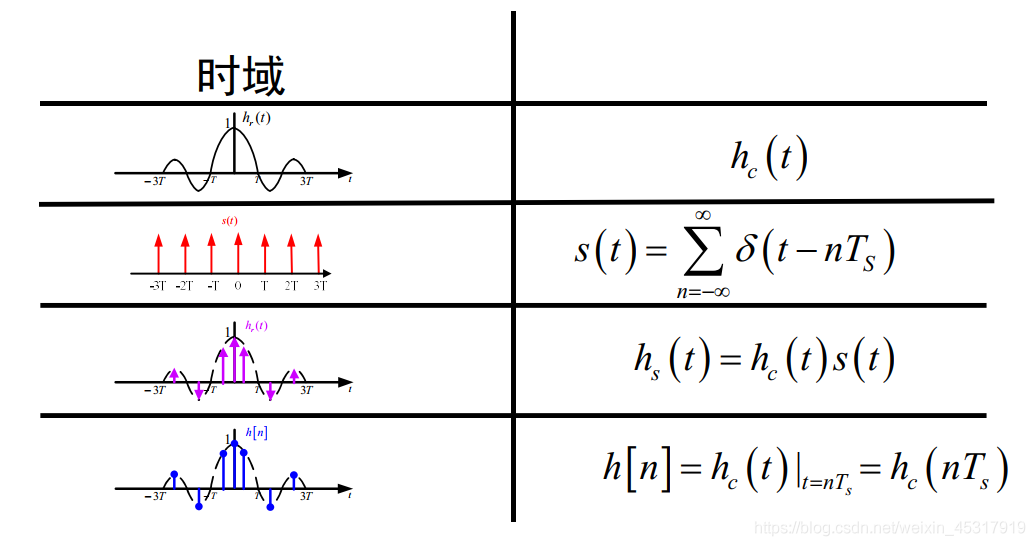
Impulse response invariant method and bilinear transformation method for IIR filter design
加点字符就能让qq昵称很酷的神奇代码?
Based on the SVM regression forecast 】 【 LibSVM realize the prediction of a characteristic data
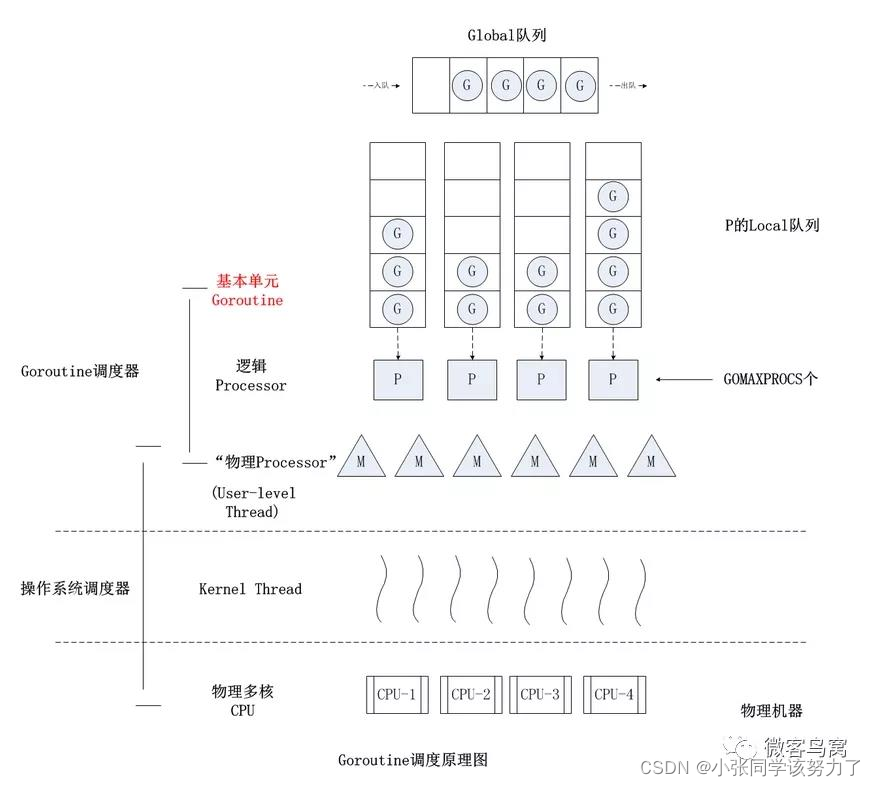
golang八股文整理(持续搬运)

2022-07-13 第五小组 瞒春 学习笔记
MATLAB file operations
集成电路实践----D触发器
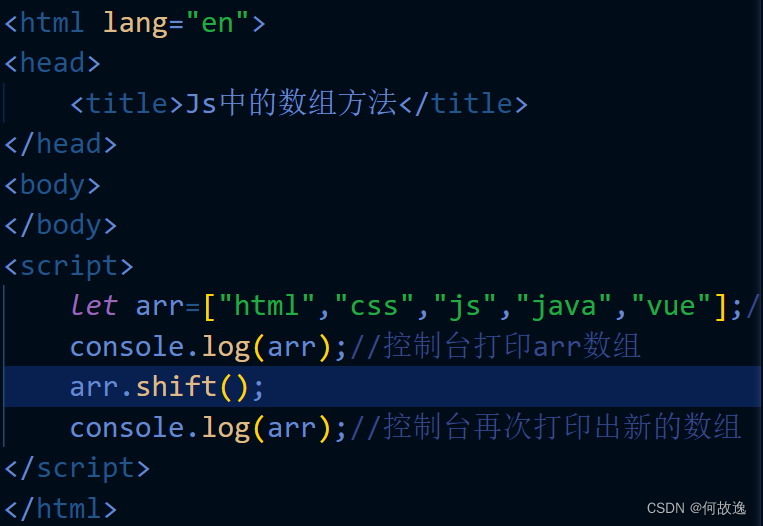
JS中的数组方法和循环

js电梯导航基础案例
随机推荐
我的第一篇博客
golang八股文整理(持续搬运)
DOM —— 事件对象
CUDA programming based on Visual Studio 2015 (1): basic configuration
加载事件的用法
电设3----脉冲信号测试仪
Jenkins 参数化构建(Extended Choice Parameter)
Golang学习(三十五) go 连接redis
2022-07-26 第六小组 瞒春 学习笔记
时频分析之Wigner-Ville分布
scroll、offset、client事件的用法及区别
web渗透之文件上传漏洞
第五章-5.2-指示器随机变量
加点字符就能让qq昵称很酷的神奇代码?
初入c语言
为什么四个字节的float表示的范围比八个字节的long要广?
什么是Knife4j?
DOM —— 事件机制及事件链
this beta version of Typora is expired, please download and install a newer version.Typora的保姆级最新解决方法
DOM —— 事件类型