当前位置：网站首页>[Linear Algebra 02] 2 interpretations of AX=b and 5 perspectives of matrix multiplication

[Linear Algebra 02] 2 interpretations of AX=b and 5 perspectives of matrix multiplication

2022-08-04 21:41:00 【Moonfish and the Fourteen Lines】

在看MITLinear algebra,感谢Gilbert Strang教授,Let me have a new understanding of linear algebra.This article starts from the corresponding course videos and textbooks,talk about interestingAX=b的2interpretation and matrix multiplication5种视角,当然,This is my personal analysis,Inspired by reserved thinking.

AX=b的2种解释

I'll just give an example,比如矩阵A和矩阵B
$\begin{bmatrix}1 &2 \\ 3&4 \end{bmatrix} \ \ \ \ \ \ B= \begin{bmatrix}6 &2 & 1\\ 4&4 &1 \\ 7 & 6 &1 \end{bmatrix}$

If we write it in the form of an equation,Assuming that matrix is better thanAThe right value of the corresponding equation is5和6,那么就有
$x_1 + 2x_2 = 5 \\ 3x_1 + 4x_2 =6$

Row Picture

With the help of the knowledge learned in junior high school,我们知道 这其实是 $x_1x_2$ Two straight lines in the plane,Two straight lines in the plane should only intersect and parallel two cases .我们可以借助matlabDraw out the two straight lines：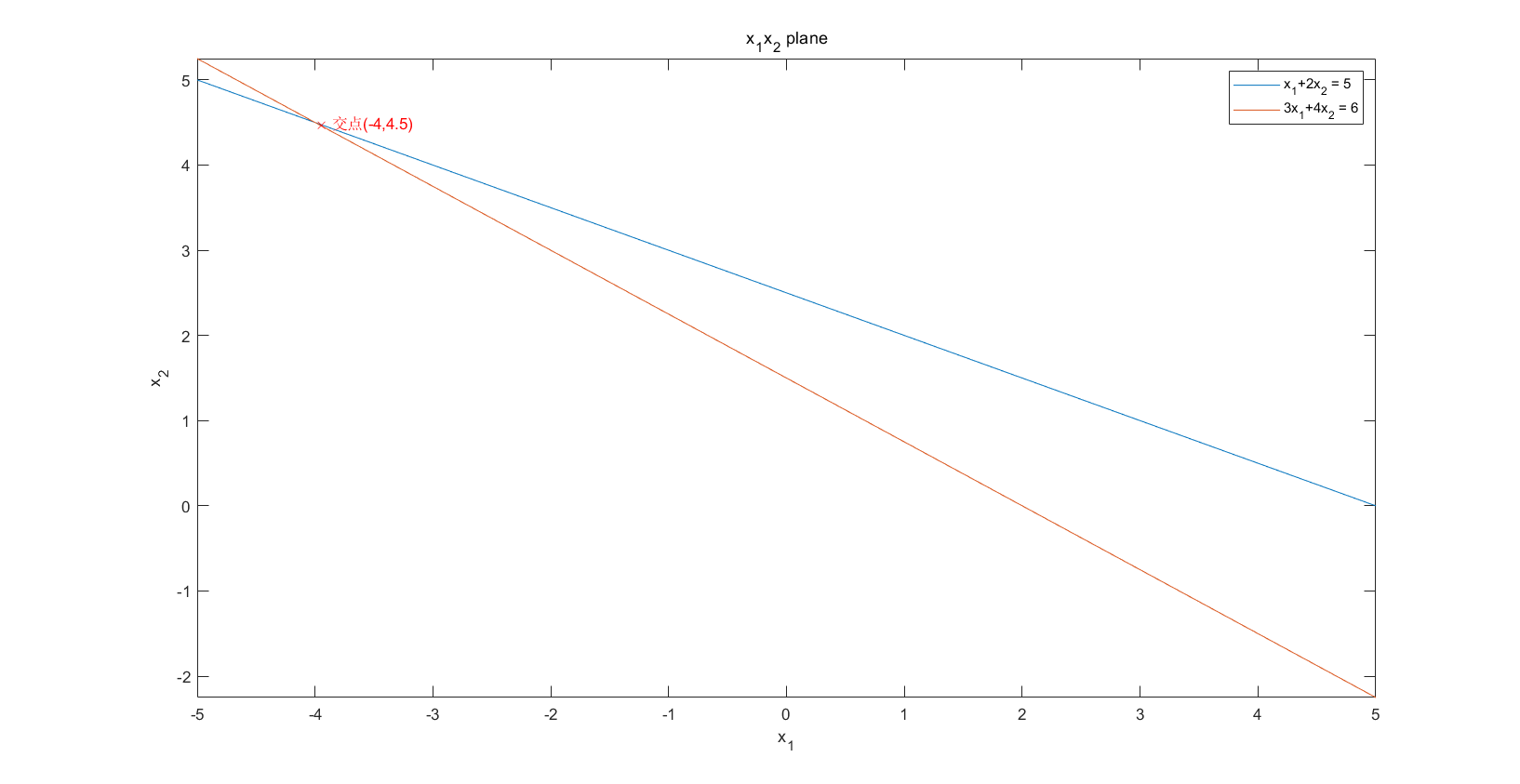
请添加图片描述

The corresponding drawing code is：

% draw two-dimensional lines

% 定义
syms x1;
y1 = 2.5-0.5*x1; y2 = 1.5-3/4*x1;
% fplot画线
fplot(y1);  hold on;  fplot(y2);
% 直线标注
legend('x_1+2x_2 = 5','3x_1+4x_2 = 6');
% solve求解交点
xp = double(solve(y1==y2)); % 转换数据格式
yp = 2.5-0.5*xp;
% Intersection callout
text(xp,yp,['\times ','交点','(',num2str(xp),',',num2str(yp),')'],Color = 'red');
% title and axis
title('x_1x_2 plane');
xlabel('x_1');
ylabel('x_2');

We can find that two lines have a point of intersection,This intersection is(-4,4.5).In fact, this intersection is also the solution of the original equation..应该说明：Correspondence between the intersection situation in this solution space and the matrix equation,就是“Row Picture”,Think of equations represented by matrices as points in space、线、面.我将其理解为Visualized solution space.

Let's look at the more complex 3D scene,假设矩阵BThe right value of the corresponding equation is8、9和10,即
$6x_1 +2x_2 + x_3= 8 \\ 4x_1 + 4x_2 + x_3=9 \\ 7x_1 + 6x_2 + x_3=10$
The corresponding drawing results and drawing codes are respectively：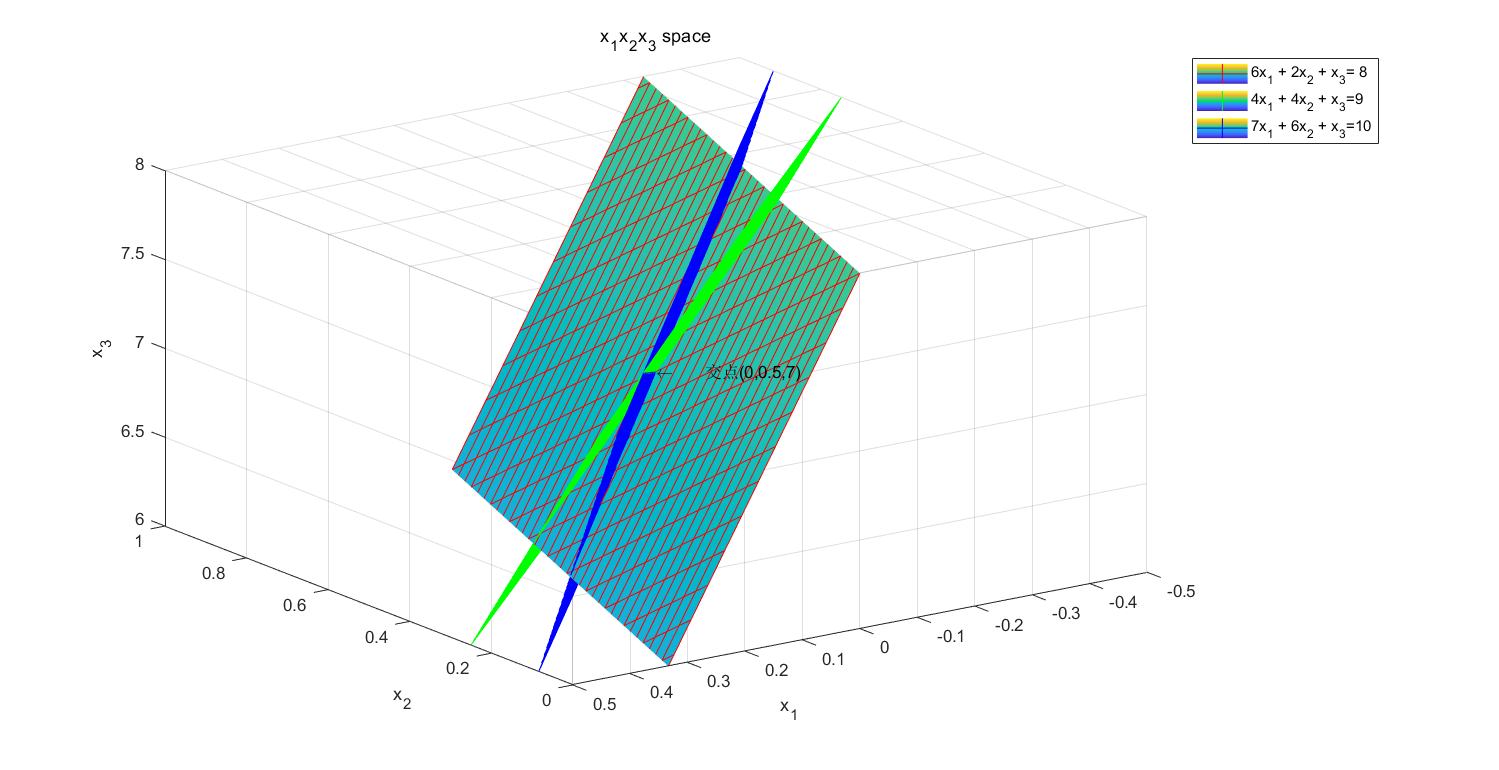
请添加图片描述

% Draw 3 d plane

% 定义
syms x1;
syms x2;
y1 = 8-6*x1-2*x2; y2 = 9-4*x1-4*x2; y3 = 10-7*x1-6*x2;
% fmesh画平面
fsurf(y1,EdgeColor='r'); hold on; fsurf(y2,EdgeColor='g'); hold on ;fsurf(y3,EdgeColor='b');
% Plane callout
legend('6x_1 + 2x_2 + x_3= 8','4x_1 + 4x_2 + x_3=9','7x_1 + 6x_2 + x_3=10');
% solve求解交点
result = solve([y1==y2,y1==y3]);
xp = double(result.x1); % 转换数据格式
yp = double(result.x2);
zp = 8-6*xp-2*yp;
% Intersection callout
text(xp,yp,zp,['\leftarrow ',' 交点','(',num2str(xp),',',num2str(yp),',',num2str(zp),')'],Color = 'black');
% title and axis
title('x_1x_2x_3 space');
xlabel('x_1'); xlim([-0.5,0.5]);
ylabel('x_2'); ylim([0,1]);
zlabel('x_3'); zlim([6,8]);

Similarly, we can find that three planes have three lines of intersection,With one hand in line with the third plane intersection is(0,0.5,7),It can also be verified that this intersection is the solution of the original equation.借助Matlab的绘图工具,We made up the hand-painted intuitive enough defect in the solution space.可以想象,对于更高维的空间,Equations represented by matrices are still points in space、Lines and Hyperplanes.

Column Picture

“Column Picture” Contains the we will matrix as the fundamental nature of linear algebra operations,That is, it should be regarded as a combination of two basic operations,i.e. addition and scalar multiplication,也即 $a\vec{x}+b\vec{y}$ 的形式.我将其理解为Weighted Sum of Matrix Columns .

Let's take a look at an explanation to understand,以矩阵AThe corresponding equation as an example：
$\begin{bmatrix}1 &2 \\ 3&4 \end{bmatrix} \begin{bmatrix}x_1 \\ x_2 \end{bmatrix} = \begin{bmatrix}5 \\ 6 \end{bmatrix}$
实际上, $x_1$ 和 $x_2$ 就是对矩阵AThe weighting coefficients assigned to the two columns in,That is, the above formula should be written as：
$x_1 \begin{bmatrix}1 \\ 3 \end{bmatrix} + x_2 \begin{bmatrix}2 \\ 4 \end{bmatrix} = \begin{bmatrix}5 \\ 6 \end{bmatrix}$
Gilbert StrangThe professor hopes that we can focus on the experience here,To really understand what is called linearity in linear algebra operations.其实,Observe the structure of this solution,We can easily think of,如果bas a result column,It is necessarily matrixALinear combination of two columns,也就是说,so-called solution of the equation,That is, it should be a group that satisfiesbMatrix column weights and coefficients for columns.feel this layer,than come up directly and tell you to follow Matrix dot product algorithm 将 $A X = b$ expand into equations,It is much better to use elimination to solve the equation,Because you discovered the meaning of linearity.

实际上,There are other ways to account for linearity as well.在这里,我们发现XAs a column matrix is placed in the matrixA的右边,This achieves the matrixA的列操作.If for general matrix multiplication,What would a column of coefficients on the right look like?？We will answer this question below.

矩阵乘法的5种视角

The problem we face is to solve matrix multiplication：
$\ \ ?$

第一视角：point multiplication rule

给出A和B的例子：
$A_1= \begin{bmatrix}1 &3 \\ 2&4 \end{bmatrix} \ \ \ \ \ \ B_1= \begin{bmatrix}5 &7 \\ 6&8 \end{bmatrix}$

Dot multiplication is widely used,But it does not directly point out that for a start,即The first left matrixiThe elements of the row are related to the right matrixjDot product of column elements as result matrixi行第j列的元素.结合例子,This idea can be expressed as：
$A_1B_1 = \begin{bmatrix}1 &3 \\ 2&4 \end{bmatrix} \begin{bmatrix}5 &7 \\ 6&8 \end{bmatrix} = \begin{bmatrix}1\times5+3\times6 &1\times7+3\times8 \\ 2\times5+4\times6 & 2\times7+4\times8 \end{bmatrix} = \begin{bmatrix}23 &31 \\ 34&46 \end{bmatrix}$

第二视角：Linear combination of rows

we answer here“What would a column of coefficients on the right look like?？”这个问题,The answer is a linear combination of pairs of rows.that will beB作为一个整体看待,而将AThe coefficients of each row are regarded as pairBBOC's weighting.
修改A和B的例子：
$A_2= \begin{bmatrix}1 \\ 3 \\ 2 \\ 4 \end{bmatrix} \ \ \ \ \ \ B_2= \begin{bmatrix}5 &7 & 6&8 \end{bmatrix}$

This idea is expressed as：
$A_2 B_2= \begin{bmatrix}1 \\ 3 \\ 2 \\ 4 \end{bmatrix} \begin{bmatrix}5 &7 & 6&8 \end{bmatrix} = \begin{bmatrix}1 \times (5 &7 & 6&8) \\ 3 \times (5 &7 & 6&8) \\ 2 \times (5 &7 & 6&8) \\ 4 \times (5 &7 & 6&8) \end{bmatrix} = \begin{bmatrix}5 &7 & 6&8 \\ 15&21 & 18&24 \\ 10 &14 & 12&16\\ 20 & 28 & 24&32 \end{bmatrix}$

第三视角：列的线性组合

其实在 $A X = b$ 的讨论中,我们已经知道了“What would a column of coefficients on the left look like?？”的答案,It should be a linear combination of columns. 修改A和B的例子为：
$A_3= \begin{bmatrix}1 &3 & 2 & 4 \end{bmatrix} \ \ \ \ \ \ B_3= \begin{bmatrix}5 \\ 7 \\ 6\\8 \end{bmatrix}$
Such ideas expressed as：
$A_3B_3= \begin{bmatrix}1 &3 & 2 & 4 \end{bmatrix} \begin{bmatrix}5 \\ 7 \\ 6\\8 \end{bmatrix} =5\times 1+7\times 3+ 6 \times2 + 8 \times 4 = 70$
This is a special enough example,容易发现,At this time, the equations obtained according to the first three perspectives will all obtain such a consistent summation formula,But they get this summation from different angles.Combining second and third perspectives,We can naturally find that a left-multiplied matrix is a linear combination of matrix rows,The right-multiplied matrix is a linear combination of the matrix columns..

第四视角：Linear combination of column and row vectors

Let's revisit $A_1B_1$ ,基于前面的理解,实际上Matrix multiplication can also be expressed as a linear combination of vector multiplication,即：

$\Sigma (column_i \ of \ A) × (row_i \ of \ B)$
即 $A_1B_1$ 可以重新写为：
$A_1B_1= \begin{bmatrix}1 &3 \\ 2&4 \end{bmatrix} \begin{bmatrix}5 &7 \\ 6&8 \end{bmatrix} = \begin{bmatrix}1 \\ 2 \end{bmatrix} \begin{bmatrix}5 &7 \end{bmatrix}+ + \begin{bmatrix}3 \\4 \end{bmatrix} \begin{bmatrix}6 &8 \end{bmatrix} = \begin{bmatrix}5 &7 \\ 10&14 \end{bmatrix} +\begin{bmatrix}18 &24 \\ 24&32 \end{bmatrix} = \begin{bmatrix}23 &31 \\ 34&46 \end{bmatrix}$
从这个角度看,We get another intuitive sense of why scalar multiplication and addition are two basic operations in linear space.

Fifth perspective：矩阵分块

For example, we need to solve the following matrix multiplication problem：
$A_4= \begin{bmatrix}1 &3 & 0 & 0\\ 2&4 & 0 & 0\\ 0& 0 &1 & 0 \\ 0& 0 & 0 &1 \end{bmatrix} \ \ \ \ \ \ B_4= \begin{bmatrix}5 &7 & 0 & 0\\ 6&8 & 0 & 0\\ 0& 0 &1 & 0 \\ 0& 0 & 0 &1 \end{bmatrix}$
Although this problem can be solved with the help of perspective 1 and perspective 4,But in fact, we can look at it from a higher perspective,即
$A_4= \begin{bmatrix}A_1& 0 \\ 0&I \end{bmatrix} \ \ \ \ \ \ B_4= \begin{bmatrix}B_1 &0 \\ 0&I \end{bmatrix}$
也就是说,After matrix block,The block matrix can be considered as an element participating in the matrix multiplication.We directly expand the solution from the first perspective,就有
$A_4 B_4= \begin{bmatrix}A_1& 0 \\ 0&I \end{bmatrix} \begin{bmatrix}B_1 &0 \\ 0&I \end{bmatrix} = \begin{bmatrix}A_1B_1+ 0 \times 0 &A_1\times0+0\times \\ 0\times B_1+I\times0& 0\times 0+I\times I \end{bmatrix} = \begin{bmatrix}A_1B_1 &0 \\ 0&I \end{bmatrix} = \begin{bmatrix}23 &31 & 0 & 0\\ 34&46 & 0 & 0\\ 0& 0 &1 & 0 \\ 0& 0 & 0 &1 \end{bmatrix}$
Results the desires of before application,It can be found that the operation has been significantly simplified.

of the above four matrix multiplicationsMatlabSolving process validation are as follows：

>> A1 = [1,3;2,4]; B1 = [5,7;6,8];
>> A1*B1

ans =

    23    31
    34    46

>> A2 = reshape(A1,[4,1]);B2 = reshape(B1,[1,4]);%reshapefunction to change matrix dimensions
>> A2*B2

ans =

     5     6     7     8
    10    12    14    16
    15    18    21    24
    20    24    28    32

>> A3 = reshape(A1,[1,4]);B3 = reshape(B1,[4,1]);
>> A3*B3

ans =

    70

>> A4 = [1,3,0,0;2,4,0,0;0,0,1,0;0,0,0,1]; B4 = [5,7,0,0;6,8,0,0;0,0,1,0;0,0,0,1];
>> A4*B4

ans =

    23    31     0     0
    34    46     0     0
     0     0     1     0
     0     0     0     1