当前位置:网站首页>Leetcode(215)——数组中的第K个最大元素
Leetcode(215)——数组中的第K个最大元素
2022-07-04 07:35:00 【SmileGuy17】
Leetcode(215)——数组中的第K个最大元素
题目
给定整数数组 nums 和整数 k,请返回数组中第 k 个最大的元素。
请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。
示例 1:
输入: [3,2,1,5,6,4] 和 k = 2
输出: 5
示例 2:输入: [3,2,3,1,2,4,5,5,6] 和 k = 4
输出: 4
提示:
- 1 1 1 <= k <= nums.length <= 1 0 4 10^4 104
- − 1 0 4 -10^4 −104 <= nums[i] <= 1 0 4 10^4 104
题解
方法一:冒泡排序
思路
冒泡排序的原理
代码实现
我的:
class Solution {
public:
int findKthLargest(vector<int>& nums, int k) {
int n = nums.size();
if(n == 1) return nums[0];
bool swapped;
for(int i = 0; i < n; i++){
swapped = false;
for(int t = 0; t < n-i-1; t++){
if(nums[t] < nums[t+1]){
swap(nums[t], nums[t+1]);
swapped = true;
}
}
if(!swapped) break;
}
return nums[k-1];
}
};
复杂度分析
时间复杂度: O ( n log n ) O(n \log n) O(nlogn)
空间复杂度: O ( 1 ) O(1) O(1)
方法二:简单选择排序
思路
简单选择排序的原理
代码实现
我的:
class Solution {
public:
int findKthLargest(vector<int>& nums, int k) {
int n = nums.size();
if(n == 1) return nums[0];
int max, tmp;
for(int i = 0; i < n; i++){
max = i;
for(int t = i+1; t < n; t++){
if(nums[max] < nums[t]) max = t;
}
tmp = nums[i];
nums[i] = nums[max];
nums[max] = tmp;
}
return nums[k-1];
}
};
复杂度分析
时间复杂度: O ( n log n ) O(n \log n) O(nlogn)
空间复杂度: O ( 1 ) O(1) O(1)
方法三:直接插入排序
思路
直接插入排序的原理
代码实现
我的:
class Solution {
public:
int findKthLargest(vector<int>& nums, int k) {
int n = nums.size();
if(n == 1) return nums[0];
for(int i = 1; i < n; i++){
// 设定第一个元素是排好序的长度为1的序列,所以从第二个元素开始排序
for(int t = i; t > 0 && nums[t] > nums[t-1]; t--)
swap(nums[t], nums[t-1]);
}
return nums[k-1];
}
};
复杂度分析
时间复杂度: O ( n log n ) O(n \log n) O(nlogn)
空间复杂度: O ( 1 ) O(1) O(1)
方法四:希尔排序
思路
希尔排序的原理
代码实现
我的:
class Solution {
public:
int findKthLargest(vector<int>& nums, int k) {
int n = nums.size();
if(n == 1) return nums[0];
int increment = n/3+1; // 保底为1
while(increment > 0){
// 直接插入排序
for(int i = 0; i < n; i++){
for(int t = i; t-increment >= 0 && nums[t] > nums[t-increment]; t -= increment)
swap(nums[t], nums[t-increment]);
}
increment--;
}
return nums[k-1];
}
};
复杂度分析
时间复杂度: O ( n 3 / 2 ) O(n^{3/2}) O(n3/2)
空间复杂度: O ( 1 ) O(1) O(1)
方法五:归并排序
思路
归并排序的原理
代码实现
我的(递归):
class Solution {
void MSort(vector<int>& nums, int l, int r){
if(l == r)
nums[l] = nums[l];
else{
vector<int> Tmp(r-l+1);
int mid = (l+r)/2;
MSort(nums, l, mid);
MSort(nums, mid+1, r);
// 将上面两个分组归并到一起
int p1 = l, p2 = mid+1, p = 0;
while(p1 <= mid && p2 <= r){
if(nums[p1] < nums[p2])
Tmp[p++] = nums[p2++];
else Tmp[p++] = nums[p1++];
}
if(p1 <= mid)
while(p1 <= mid) Tmp[p++] = nums[p1++];
if(p2 <= r)
while(p2 <= r) Tmp[p++] = nums[p2++];
p = 0;
while(l <= r)
nums[l++] = Tmp[p++];
}
}
public:
int findKthLargest(vector<int>& nums, int k) {
if(nums.size() == 1) return nums[0];
// for(int i = 0; i < n; i++){}
// 归并排序
MSort(nums, 0, nums.size()-1);
return nums[k-1];
}
};
复杂度分析
时间复杂度: O ( n log n ) O(n \log n) O(nlogn)
空间复杂度: O ( n ) O(n) O(n)
方法六:快速排序(改进——「快速选择」算法)
思路
必须要有打乱数组的操作,即枢轴选取不固定,否则容易遇到极端情况导致时间复杂度为 O ( n 2 ) O(n^2) O(n2)。
我们可以用快速排序来解决这个问题,先对原数组排序,再返回倒数第 k k k 个位置,这样平均时间复杂度是 O ( n log n ) O(n \log n) O(nlogn),但其实我们可以做的更快。
首先我们来回顾一下快速排序,这是一个典型的分治算法。我们对数组 a [ l ⋯ r ] a[l \cdots r] a[l⋯r] 做快速排序的过程是(参考《算法导论》):
- 分解: 将数组 a [ l ⋯ r ] a[l \cdots r] a[l⋯r] 「划分」成两个子数组 a [ l ⋯ q − 1 ] a[l \cdots q - 1] a[l⋯q−1]]、 a [ q + 1 ⋯ r ] a[q + 1 \cdots r] a[q+1⋯r],使得 a [ l ⋯ q − 1 ] a[l \cdots q - 1] a[l⋯q−1] 中的每个元素小于等于 a [ q ] a[q] a[q],且 a [ q ] a[q] a[q] 小于等于 a [ q + 1 ⋯ r ] a[q + 1 \cdots r] a[q+1⋯r] 中的每个元素。其中,计算下标 q q q 也是「划分」过程的一部分。
- 解决: 通过递归调用快速排序,对子数组 a [ l ⋯ q − 1 ] a[l \cdots q - 1] a[l⋯q−1] 和 a [ q + 1 ⋯ r ] a[q + 1 \cdots r] a[q+1⋯r] 进行排序。
- 合并: 因为子数组都是原址排序的,所以不需要进行合并操作, a [ l ⋯ r ] a[l \cdots r] a[l⋯r] 已经有序。
- 上文中提到的 「划分」 过程是:从子数组 a [ l ⋯ r ] a[l \cdots r] a[l⋯r] 中选择任意一个元素 x x x 作为主元,调整子数组的元素使得左边的元素都小于等于它,右边的元素都大于等于它, x x x 的最终位置就是 q q q。
由此可以发现每次经过「划分」操作后,我们一定可以确定一个元素的最终位置,即 x x x 的最终位置为 q q q,并且保证 a [ l ⋯ q − 1 ] a[l \cdots q - 1] a[l⋯q−1] 中的每个元素小于等于 a [ q ] a[q] a[q],且 a [ q ] a[q] a[q] 小于等于 a [ q + 1 ⋯ r ] a[q + 1 \cdots r] a[q+1⋯r] 中的每个元素。所以只要某次划分的 q q q 为倒数第 k k k 个下标的时候,我们就已经找到了答案。 我们只关心这一点,至于 a [ l ⋯ q − 1 ] a[l \cdots q - 1] a[l⋯q−1] 和 a [ q + 1 ⋯ r ] a[q+1 \cdots r] a[q+1⋯r] 是否是有序的,我们不关心。
因此,我们可以改进快速排序算法来解决这个问题:
在分解的过程当中,我们会对子数组进行划分,如果划分得到的 q q q 正好就是我们需要的下标(即当划分完后遇到 k == q-1,此时 a [ q ] a[q] a[q] 左边的 k − 1 k-1 k−1 个元素都大于等于它,右边的元素都小于等于它),就直接返回 a [ q ] a[q] a[q];否则,如果 q q q 比目标下标小,就递归右子区间,否则递归左子区间。
这样就可以把原来递归两个区间变成只递归一个区间,提高了时间效率。这就是「快速选择」算法。
我们知道快速排序的性能和「划分」出的子数组的长度密切相关。直观地理解如果每次规模为 n n n 的问题我们都划分成 1 1 1 和 n − 1 n - 1 n−1,每次递归的时候又向 n − 1 n - 1 n−1 的集合中递归,这种情况是最坏的,时间代价是 O ( n 2 ) O(n ^ 2) O(n2)。我们可以引入随机化来加速这个过程,它的时间代价的期望是 O ( n ) O(n) O(n),证明过程可以参考「《算法导论》9.2:期望为线性的选择算法」。
代码实现
Leetcode 官方题解:
class Solution {
public:
int quickSelect(vector<int>& a, int l, int r, int index) {
int q = randomPartition(a, l, r);
if (q == index) {
return a[q];
} else {
return q < index ? quickSelect(a, q + 1, r, index) : quickSelect(a, l, q - 1, index);
}
}
inline int randomPartition(vector<int>& a, int l, int r) {
int i = rand() % (r - l + 1) + l;
swap(a[i], a[r]);
return partition(a, l, r);
}
inline int partition(vector<int>& a, int l, int r) {
int x = a[r], i = l - 1;
for (int j = l; j < r; ++j) {
if (a[j] <= x) {
swap(a[++i], a[j]);
}
}
swap(a[i + 1], a[r]);
return i + 1;
}
int findKthLargest(vector<int>& nums, int k) {
srand(time(0));
return quickSelect(nums, 0, nums.size() - 1, nums.size() - k);
}
};
我的(递归):
class Solution {
int Partition(vector<int>& nums, int l, int r){
// 打乱数组,采用三数取中
int mid = l+(r-l)/2;
if(nums[l] > nums[r]) swap(nums[l], nums[r]);
if(nums[mid] > nums[r]) swap(nums[mid], nums[r]);
if(nums[mid] > nums[l]) swap(nums[mid], nums[l]);
// 此时nums[l]为三个数字的中位数
int privot = nums[l]; // 选取第一个为枢轴
while(l < r){
while(l < r && nums[r] <= privot)
r--;
nums[l] = nums[r];
while(l < r && nums[l] >= privot)
l++;
nums[r] = nums[l];
}
nums[l] = privot;
return l;
}
void Quicksort(vector<int>& nums, int l, int r){
if(l < r){
int privot = Partition(nums, l, r); // 获取枢轴
Quicksort(nums, l, privot-1);
Quicksort(nums, privot+1, r);
}
}
public:
int findKthLargest(vector<int>& nums, int k) {
if(nums.size() == 1) return nums[0];
// 快速排序
Quicksort(nums, 0, nums.size()-1);
return nums[k-1];
}
};
复杂度分析
时间复杂度:Leetcode 官方题解的时间复杂度为 O ( n ) O(n) O(n)。常规快速排序的平均时间复杂度为 O ( n log n ) O(n \log n) O(nlogn)。
空间复杂度: O ( log n ) O(\log n) O(logn),递归使用栈空间的空间代价的期望为 O ( log n ) O(\log n) O(logn)。
方法七:堆排序
思路
构建一个大顶堆,然后删除 k − 1 k-1 k−1 个堆顶元素,则此时的堆顶元素为第 k k k 大的元素。
代码实现
Leetcode 官方题解:
class Solution {
public:
void maxHeapify(vector<int>& a, int i, int heapSize) {
int l = i * 2 + 1, r = i * 2 + 2, largest = i;
if (l < heapSize && a[l] > a[largest]) {
largest = l;
}
if (r < heapSize && a[r] > a[largest]) {
largest = r;
}
if (largest != i) {
swap(a[i], a[largest]);
maxHeapify(a, largest, heapSize);
}
}
void buildMaxHeap(vector<int>& a, int heapSize) {
for (int i = heapSize / 2; i >= 0; --i) {
maxHeapify(a, i, heapSize);
}
}
int findKthLargest(vector<int>& nums, int k) {
int heapSize = nums.size();
buildMaxHeap(nums, heapSize);
for (int i = nums.size() - 1; i >= nums.size() - k + 1; --i) {
swap(nums[0], nums[i]);
--heapSize;
maxHeapify(nums, 0, heapSize);
}
return nums[0];
}
};
复杂度分析
时间复杂度: O ( n log n ) O(n \log n) O(nlogn),建堆的时间代价是 O ( n ) O(n) O(n),删除的总代价是 O ( k log n ) O(k \log n) O(klogn),因为 k < n k < n k<n,故渐进时间复杂为 O ( n + k log n ) O(n + k \log n) O(n+klogn) 化简为 O ( n log n ) O(n \log n) O(nlogn)。
空间复杂度: O ( log n ) O(\log n) O(logn),即递归写法使用栈空间的空间代价。
边栏推荐
- University stage summary
- Status of the thread
- Write a thread pool by hand, and take you to learn the implementation principle of ThreadPoolExecutor thread pool
- 2022-021rts: from the second half of the year
- MySQL error resolution - error 1261 (01000): row 1 doesn't contain data for all columns
- Zabbix agent主动模式的实现
- 21个战略性目标实例,推动你的公司快速发展
- Four sets of APIs for queues
- 深入浅出:了解时序数据库 InfluxDB
- Rhcsa day 3
猜你喜欢
Comparison between applet framework and platform compilation

The cloud native programming challenge ended, and Alibaba cloud launched the first white paper on application liveliness technology in the field of cloud native
Rhcsa day 3

大学阶段总结
BUUCTF(3)
【森城市】GIS数据漫谈(一)

Summary of MySQL common judgment functions!! Have you used it
![[Mori city] random talk on GIS data (I)](/img/e4/2a2ceb10a2c0285cdd0c922f827930.png)
[Mori city] random talk on GIS data (I)

Splicing plain text into JSON strings - easy language method
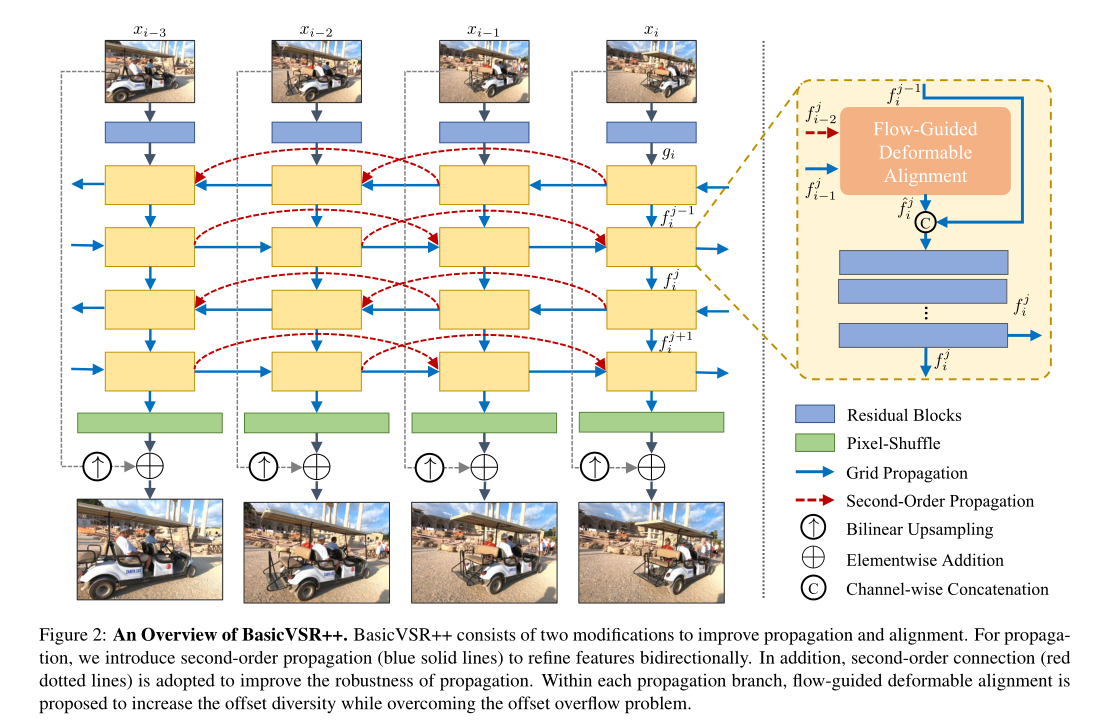
BasicVSR++: Improving Video Super-Resolutionwith Enhanced Propagation and Alignment
随机推荐
Advanced MySQL: Basics (5-8 Lectures)
This article is enough for learning advanced mysql
Implementation of ZABBIX agent active mode
What are the work contents of operation and maintenance engineers? Can you list it in detail?
A real penetration test
[MySQL transaction]
MYCAT middleware installation and use
[kubernetes series] kubesphere is installed on kubernetes
在所有SwiftUI版本(1.0-4.0)中原生实现Charts图表视图之思路
[real case] how to deal with the failure of message consumption?
Book list | as the technical support Party of the Winter Olympics, Alibaba cloud's technology is written in these books!
Boosting the Performance of Video Compression Artifact Reduction with Reference Frame Proposals and
In the era of low code development, is it still needed?
Zhanrui tankbang | jointly build, cooperate and win-win zhanrui core ecology
[network security] what is emergency response? What indicators should you pay attention to in emergency response?
Oceanbase is the leader in the magic quadrant of China's database in 2021
L1-028 judging prime number (10 points)
Technical experts from large factories: common thinking models in architecture design
Text processing function sorting in mysql, quick search of collection
Zephyr study notes 2, scheduling