当前位置:网站首页>[set theory] order relation (eight special elements in partial order relation | ① maximum element | ② minimum element | ③ maximum element | ④ minimum element | ⑤ upper bound | ⑥ lower bound | ⑦ minimu
[set theory] order relation (eight special elements in partial order relation | ① maximum element | ② minimum element | ③ maximum element | ④ minimum element | ⑤ upper bound | ⑥ lower bound | ⑦ minimu
2022-07-03 09:15:00 【Programmer community】
List of articles
- One 、 The biggest dollar
- Two 、 Minimum element
- 3、 ... and 、 The biggest dollar 、 Minimum element example
- Four 、 Great dollar
- 5、 ... and 、 Minima
- 6、 ... and 、 Great dollar 、 Minimal element example
- 7、 ... and 、 upper bound
- 8、 ... and 、 Lower bound
- Nine 、 upper bound 、 Lower bound example
- Ten 、 Upper bound ( Minimum upper bound )
- 11、 ... and 、 Lower bound ( Maximum lower bound )
- Twelve 、 Upper bound 、 Infimum example
One 、 The biggest dollar
<
A
,
≼
>
<A, \preccurlyeq>
<A,≼> yes Posets ,
B
⊆
A
B \subseteq A
B⊆A ,
y
∈
B
y \in B
y∈B ,
B
B
B All elements in are related to
y
y
y Are comparable ,
B
B
B Any element in
x
x
x , All satisfied with
x
x
x Less than or equal to
y
y
y
Symbolize :
∀
x
(
x
∈
B
→
x
≼
y
)
\forall x ( x \in B \to x \preccurlyeq y )
∀x(x∈B→x≼y)
call
y
y
y yes
B
B
B The largest element of a set ;
Two 、 Minimum element
<
A
,
≼
>
<A, \preccurlyeq>
<A,≼> yes Posets ,
B
⊆
A
B \subseteq A
B⊆A ,
y
∈
B
y \in B
y∈B ,
B
B
B All elements in are related to
y
y
y Are comparable ,
B
B
B Any element in
x
x
x , All satisfied with
y
y
y Less than or equal to
x
x
x
Symbolize :
∀
x
(
x
∈
B
→
y
≼
x
)
\forall x ( x \in B \to y \preccurlyeq x )
∀x(x∈B→y≼x)
call
y
y
y yes
B
B
B The smallest element of a set ;
3、 ... and 、 The biggest dollar 、 Minimum element example
aggregate
A
=
{
1
,
2
,
3
,
4
,
5
,
6
,
9
,
10
,
15
}
A = \{ 1, 2, 3, 4, 5, 6, 9, 10, 15 \}
A={ 1,2,3,4,5,6,9,10,15} ,
aggregate
A
A
A On the division relationship “
∣
|
∣” It's a partial order relationship ,
Poset is
<
A
,
∣
>
<A, |>
<A,∣>
x
x
x to be divisible by
y
y
y ,
x
x
x It's a divisor ( The denominator ) ,
y
y
y It's a dividend ( molecular ) ;
y
x
\dfrac{y}{x}
xy
y
y
y Can be
x
x
x to be divisible by ,
x
x
x It's a divisor ( The denominator ) ,
y
y
y It's a dividend ( molecular ) ;
y
x
\dfrac{y}{x}
xy
Draw the above partially ordered set of hastu :
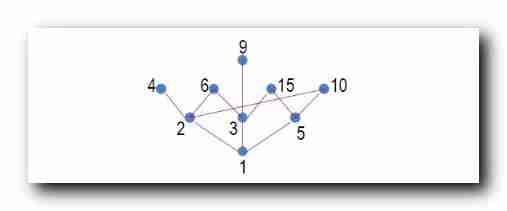
B
1
=
{
1
,
2
,
3
}
B_1 = \{ 1,2,3 \}
B1={ 1,2,3}
B
2
=
{
3
,
5
,
15
}
B_2 = \{ 3 , 5, 15 \}
B2={ 3,5,15}
B
3
=
A
B_3 = A
B3=A
Find the The biggest dollar , Minimum element ?
B
1
=
{
1
,
2
,
3
}
B_1 = \{ 1,2,3 \}
B1={ 1,2,3}
- The biggest dollar :
2
,
3
2, 3
2,3 Not comparable to each other , There is no maximum yuan ;
- Minimum element :
1
1
1 It is comparable with other elements , Are less than or equal to other elements ,
1
1
1 It's the smallest element ;
B
2
=
{
3
,
5
,
15
}
B_2 = \{ 3 , 5, 15 \}
B2={ 3,5,15}
- The biggest dollar :
15
15
15 It is comparable with other elements , Are greater than or equal to other elements ,
15
15
15 Is the largest yuan ;
- Minimum element :
3
,
5
3, 5
3,5 Not comparable to each other , There is no minimum element ;
B
3
=
A
=
{
1
,
2
,
3
,
4
,
5
,
6
,
9
,
10
,
15
}
B_3 = A = \{ 1, 2, 3, 4, 5, 6, 9, 10, 15 \}
B3=A={ 1,2,3,4,5,6,9,10,15}
- The biggest dollar :
9
,
4
,
6
,
15
,
10
9,4,6,15,10
9,4,6,15,10 Not comparable to each other , There is no maximum yuan ;
- Minimum element :
1
1
1 It is comparable with other elements , Are less than or equal to other elements ,
1
1
1 It's the smallest element ;
Four 、 Great dollar
<
A
,
≼
>
<A, \preccurlyeq>
<A,≼> yes Posets ,
B
⊆
A
B \subseteq A
B⊆A ,
y
∈
B
y \in B
y∈B ,
stay
B
B
B There is no better than
y
y
y The bigger element ,
Symbolize :
∀
x
(
x
∈
B
∧
y
≼
x
→
x
=
y
)
\forall x ( x \in B \land y \preccurlyeq x \to x = y )
∀x(x∈B∧y≼x→x=y)
call
y
y
y yes
B
B
B A collection of Great dollar ;
5、 ... and 、 Minima
<
A
,
≼
>
<A, \preccurlyeq>
<A,≼> yes Posets ,
B
⊆
A
B \subseteq A
B⊆A ,
y
∈
B
y \in B
y∈B ,
stay
B
B
B There is no better than
y
y
y Smaller elements ,
Symbolize :
∀
x
(
x
∈
B
∧
x
≼
y
→
x
=
y
)
\forall x ( x \in B \land x \preccurlyeq y \to x = y )
∀x(x∈B∧x≼y→x=y)
call
y
y
y yes
B
B
B A collection of Minima ;
6、 ... and 、 Great dollar 、 Minimal element example
aggregate
A
=
{
1
,
2
,
3
,
4
,
5
,
6
,
9
,
10
,
15
}
A = \{ 1, 2, 3, 4, 5, 6, 9, 10, 15 \}
A={ 1,2,3,4,5,6,9,10,15} ,
aggregate
A
A
A On the division relationship “
∣
|
∣” It's a partial order relationship ,
Poset is
<
A
,
∣
>
<A, |>
<A,∣>
x
x
x to be divisible by
y
y
y ,
x
x
x It's a divisor ( The denominator ) ,
y
y
y It's a dividend ( molecular ) ;
y
x
\dfrac{y}{x}
xy
y
y
y Can be
x
x
x to be divisible by ,
x
x
x It's a divisor ( The denominator ) ,
y
y
y It's a dividend ( molecular ) ;
y
x
\dfrac{y}{x}
xy
Draw the above partially ordered set of hastu :

B
1
=
{
1
,
2
,
3
}
B_1 = \{ 1,2,3 \}
B1={ 1,2,3}
B
2
=
{
3
,
5
,
15
}
B_2 = \{ 3 , 5, 15 \}
B2={ 3,5,15}
B
3
=
A
B_3 = A
B3=A
Find the Great dollar , Minima ?
B
1
=
{
1
,
2
,
3
}
B_1 = \{ 1,2,3 \}
B1={ 1,2,3}
- Great dollar :
2
,
3
2, 3
2,3 Not comparable to each other , There's nothing like
2
,
3
2,3
2,3 The bigger element ,
2
,
3
2,3
2,3 It's a huge yuan ;
- Minima :
1
1
1 It is comparable with other elements , Are less than or equal to other elements , There's nothing like
1
1
1 Smaller elements ,
1
1
1 Is a minimal element ;
B
2
=
{
3
,
5
,
15
}
B_2 = \{ 3 , 5, 15 \}
B2={ 3,5,15}
- Great dollar :
15
15
15 It is comparable with other elements , Are greater than or equal to other elements , There's nothing like
15
15
15 The bigger element ,
15
15
15 yes Great dollar ;
- Minimum element :
3
,
5
3, 5
3,5 Not comparable to each other , There's nothing like
3
,
5
3,5
3,5 Smaller elements ,
3
,
5
3,5
3,5 Is a minimal element ;
B
3
=
A
=
{
1
,
2
,
3
,
4
,
5
,
6
,
9
,
10
,
15
}
B_3 = A = \{ 1, 2, 3, 4, 5, 6, 9, 10, 15 \}
B3=A={ 1,2,3,4,5,6,9,10,15}
- Great dollar :
9
,
4
,
6
,
15
,
10
9,4,6,15,10
9,4,6,15,10 Not comparable to each other , There's nothing like
9
,
4
,
6
,
15
,
10
9,4,6,15,10
9,4,6,15,10 The bigger element ,
9
,
4
,
6
,
15
,
10
9,4,6,15,10
9,4,6,15,10 It's a huge yuan ;
- Minima :
1
1
1 It is comparable with other elements , Are less than or equal to other elements , There's nothing like
1
1
1 Smaller elements ,
1
1
1 Is a minimal element ;
7、 ... and 、 upper bound
<
A
,
≼
>
<A, \preccurlyeq>
<A,≼> yes Posets ,
B
⊆
A
B \subseteq A
B⊆A ,
y
∈
A
y \in A
y∈A
y
y
y Than
B
B
B All elements in should be big
Symbolize :
∀
x
(
x
∈
B
→
x
≼
y
)
\forall x ( x \in B \to x \preccurlyeq y )
∀x(x∈B→x≼y)
call
y
y
y yes
B
B
B A collection of upper bound ;
8、 ... and 、 Lower bound
<
A
,
≼
>
<A, \preccurlyeq>
<A,≼> yes Posets ,
B
⊆
A
B \subseteq A
B⊆A ,
y
∈
A
y \in A
y∈A
y
y
y Than
B
B
B All elements in should be small
Symbolize :
∀
x
(
x
∈
B
→
y
≼
x
)
\forall x ( x \in B \to y \preccurlyeq x )
∀x(x∈B→y≼x)
call
y
y
y yes
B
B
B A collection of Lower bound ;
Nine 、 upper bound 、 Lower bound example
aggregate
A
=
{
1
,
2
,
3
,
4
,
5
,
6
,
9
,
10
,
15
}
A = \{ 1, 2, 3, 4, 5, 6, 9, 10, 15 \}
A={ 1,2,3,4,5,6,9,10,15} ,
aggregate
A
A
A On the division relationship “
∣
|
∣” It's a partial order relationship ,
Poset is
<
A
,
∣
>
<A, |>
<A,∣>
x
x
x to be divisible by
y
y
y ,
x
x
x It's a divisor ( The denominator ) ,
y
y
y It's a dividend ( molecular ) ;
y
x
\dfrac{y}{x}
xy
y
y
y Can be
x
x
x to be divisible by ,
x
x
x It's a divisor ( The denominator ) ,
y
y
y It's a dividend ( molecular ) ;
y
x
\dfrac{y}{x}
xy
Draw the above partially ordered set of hastu :

B
1
=
{
1
,
2
,
3
}
B_1 = \{ 1,2,3 \}
B1={ 1,2,3}
B
2
=
{
3
,
5
,
15
}
B_2 = \{ 3 , 5, 15 \}
B2={ 3,5,15}
B
3
=
A
B_3 = A
B3=A
Find the upper bound , Lower bound ?
B
1
=
{
1
,
2
,
3
}
B_1 = \{ 1,2,3 \}
B1={ 1,2,3}
- upper bound :
6
6
6 And
1
,
2
,
3
1, 2, 3
1,2,3 Comparable ,
6
6
6 Than
B
1
B_1
B1 All elements in the are big ,
6
6
6 It's the upper bound ;
- Lower bound :
1
1
1 And
1
,
2
,
3
1, 2, 3
1,2,3 Comparable ,
1
1
1 Than
B
1
B_1
B1 All elements in are small ,
1
1
1 It's the lower boundary ;
B
2
=
{
3
,
5
,
15
}
B_2 = \{ 3 , 5, 15 \}
B2={ 3,5,15}
- upper bound :
15
15
15 And
3
,
5
,
15
3 , 5, 15
3,5,15 Comparable ,
15
15
15 Than
B
2
B_2
B2 All elements in the are big ,
15
15
15 It's the upper bound ;
- Lower bound :
1
1
1 And
3
,
5
,
15
3 , 5, 15
3,5,15 Comparable ,
1
1
1 Than
B
2
B_2
B2 All elements in are small ,
1
1
1 It's the lower boundary ;
B
3
=
A
=
{
1
,
2
,
3
,
4
,
5
,
6
,
9
,
10
,
15
}
B_3 = A = \{ 1, 2, 3, 4, 5, 6, 9, 10, 15 \}
B3=A={ 1,2,3,4,5,6,9,10,15}
- upper bound : There are no elements and
B
3
B_3
B3 The elements in are comparable ; There is no upper bound ;
- Lower bound :
1
1
1 And
B
3
B_3
B3 The elements in are comparable ,
1
1
1 Than
B
3
B_3
B3 All elements in are small ,
1
1
1 It's the lower boundary ;
Ten 、 Upper bound ( Minimum upper bound )
<
A
,
≼
>
<A, \preccurlyeq>
<A,≼> yes Posets ,
B
⊆
A
B \subseteq A
B⊆A ,
y
∈
A
y \in A
y∈A
The smallest element in the upper bound is Minimum upper bound , Also known as supremum
11、 ... and 、 Lower bound ( Maximum lower bound )
<
A
,
≼
>
<A, \preccurlyeq>
<A,≼> yes Posets ,
B
⊆
A
B \subseteq A
B⊆A ,
y
∈
A
y \in A
y∈A
The biggest element in the lower bound is Maximum lower bound , Also known as infimum
Twelve 、 Upper bound 、 Infimum example
aggregate
A
=
{
1
,
2
,
3
,
4
,
5
,
6
,
9
,
10
,
15
}
A = \{ 1, 2, 3, 4, 5, 6, 9, 10, 15 \}
A={ 1,2,3,4,5,6,9,10,15} ,
aggregate
A
A
A On the division relationship “
∣
|
∣” It's a partial order relationship ,
Poset is
<
A
,
∣
>
<A, |>
<A,∣>
x
x
x to be divisible by
y
y
y ,
x
x
x It's a divisor ( The denominator ) ,
y
y
y It's a dividend ( molecular ) ;
y
x
\dfrac{y}{x}
xy
y
y
y Can be
x
x
x to be divisible by ,
x
x
x It's a divisor ( The denominator ) ,
y
y
y It's a dividend ( molecular ) ;
y
x
\dfrac{y}{x}
xy
Draw the above partially ordered set of hastu :

B
1
=
{
1
,
2
,
3
}
B_1 = \{ 1,2,3 \}
B1={ 1,2,3}
B
2
=
{
3
,
5
,
15
}
B_2 = \{ 3 , 5, 15 \}
B2={ 3,5,15}
B
3
=
A
B_3 = A
B3=A
Find the Upper bound ( Minimum upper bound ) , Lower bound ( Maximum lower bound ) ?
B
1
=
{
1
,
2
,
3
}
B_1 = \{ 1,2,3 \}
B1={ 1,2,3}
- Upper bound :
6
6
6 And
1
,
2
,
3
1, 2, 3
1,2,3 Comparable ,
6
6
6 Than
B
1
B_1
B1 All elements in the are big ,
6
6
6 It's the upper bound ;
6
6
6 It is also the supremum , Minimum upper bound ;
- Lower bound :
1
1
1 And
1
,
2
,
3
1, 2, 3
1,2,3 Comparable ,
1
1
1 Than
B
1
B_1
B1 All elements in are small ,
1
1
1 It's the lower boundary ;
1
1
1 It is also the infimum , Maximum lower bound ;
B
2
=
{
3
,
5
,
15
}
B_2 = \{ 3 , 5, 15 \}
B2={ 3,5,15}
- Upper bound :
15
15
15 And
3
,
5
,
15
3 , 5, 15
3,5,15 Comparable ,
15
15
15 Than
B
2
B_2
B2 All elements in the are big ,
15
15
15 It's the upper bound ;
15
15
15 It is also the supremum , Minimum upper bound ;
- Lower bound :
1
1
1 And
3
,
5
,
15
3 , 5, 15
3,5,15 Comparable ,
1
1
1 Than
B
2
B_2
B2 All elements in are small ,
1
1
1 It's the lower boundary ;
1
1
1 It is also the infimum , Maximum lower bound ;
B
3
=
A
=
{
1
,
2
,
3
,
4
,
5
,
6
,
9
,
10
,
15
}
B_3 = A = \{ 1, 2, 3, 4, 5, 6, 9, 10, 15 \}
B3=A={ 1,2,3,4,5,6,9,10,15}
- Upper bound : There are no elements and
B
3
B_3
B3 The elements in are comparable ; There is no upper bound ; non-existent Upper bound / Minimum upper bound ;
- Lower bound :
1
1
1 And
B
3
B_3
B3 The elements in are comparable ,
1
1
1 Than
B
3
B_3
B3 All elements in are small ,
1
1
1 It's the lower boundary ;
1
1
1 It is also the infimum , Maximum lower bound ;
边栏推荐
- Pic16f648a-e/ss PIC16 8-bit microcontroller, 7KB (4kx14)
- [point cloud processing paper crazy reading classic version 14] - dynamic graph CNN for learning on point clouds
- DOM render mount patch responsive system
- 拯救剧荒,程序员最爱看的高分美剧TOP10
- Discussion on enterprise informatization construction
- Bert install no package metadata was found for the 'sacraments' distribution
- [point cloud processing paper crazy reading classic version 11] - mining point cloud local structures by kernel correlation and graph pooling
- LeetCode 324. 摆动排序 II
- LeetCode 57. Insert interval
- [point cloud processing paper crazy reading cutting-edge version 12] - adaptive graph revolution for point cloud analysis
猜你喜欢

LeetCode 715. Range module
We have a common name, XX Gong

一个优秀速开发框架是什么样的?
![[point cloud processing paper crazy reading cutting-edge version 12] - adaptive graph revolution for point cloud analysis](/img/c6/5f723d9021cf684dcfb662ed3acaec.png)
[point cloud processing paper crazy reading cutting-edge version 12] - adaptive graph revolution for point cloud analysis

LeetCode 438. Find all letter ectopic words in the string
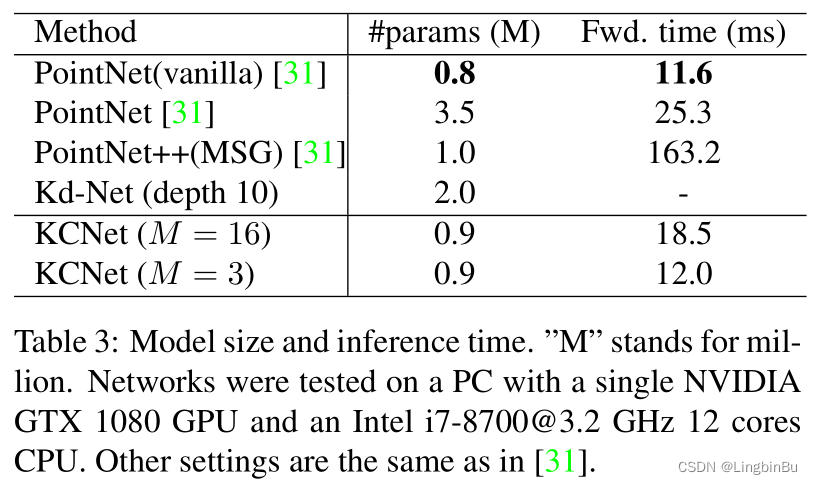
【点云处理之论文狂读经典版11】—— Mining Point Cloud Local Structures by Kernel Correlation and Graph Pooling

2022-1-6 Niuke net brush sword finger offer

Basic knowledge of network security
2022-2-13 learn the imitation Niuke project - Project debugging skills
![[advanced feature learning on point clouds using multi resolution features and learning]](/img/f0/abed28e94eb4a95c716ab8cecffe04.png)
[advanced feature learning on point clouds using multi resolution features and learning]
随机推荐
【点云处理之论文狂读前沿版12】—— Adaptive Graph Convolution for Point Cloud Analysis
Divide candy (circular queue)
Jenkins learning (I) -- Jenkins installation
2022-2-14 learning xiangniuke project - Session Management
2022-2-13 learning xiangniuke project - version control
状态压缩DP AcWing 91. 最短Hamilton路径
LeetCode 532. 数组中的 k-diff 数对
数位统计DP AcWing 338. 计数问题
低代码前景可期,JNPF灵活易用,用智能定义新型办公模式
[point cloud processing paper crazy reading frontier version 11] - unsupervised point cloud pre training via occlusion completion
教育信息化步入2.0,看看JNPF如何帮助教师减负,提高效率?
Low code momentum, this information management system development artifact, you deserve it!
CSDN markdown editor help document
State compression DP acwing 291 Mondrian's dream
LeetCode 535. TinyURL 的加密与解密
What is an excellent fast development framework like?
[point cloud processing paper crazy reading frontier version 8] - pointview gcn: 3D shape classification with multi view point clouds
【点云处理之论文狂读经典版14】—— Dynamic Graph CNN for Learning on Point Clouds
Discussion on enterprise informatization construction
The "booster" of traditional office mode, Building OA office system, was so simple!