当前位置:网站首页>Leetcode(547)——省份数量
Leetcode(547)——省份数量
2022-07-06 16:50:00 【SmileGuy17】
Leetcode(547)——省份数量
题目
有 n n n 个城市,其中一些彼此相连,另一些没有相连。如果城市 a a a 与城市 b b b 直接相连,且城市 b b b 与城市 c c c 直接相连,那么城市 a a a 与城市 c c c 间接相连。
省份 是一组直接或间接相连的城市,组内不含其他没有相连的城市。
给你一个 n × n n \times n n×n 的矩阵 i s C o n n e c t e d isConnected isConnected,其中 i s C o n n e c t e d [ i ] [ j ] = 1 isConnected[i][j] = 1 isConnected[i][j]=1 表示第 i i i 个城市和第 j j j 个城市直接相连,而 i s C o n n e c t e d [ i ] [ j ] = 0 isConnected[i][j] = 0 isConnected[i][j]=0 表示二者不直接相连。
返回矩阵中 省份 的数量。
示例 1:
输入:isConnected = [[1,1,0],[1,1,0],[0,0,1]]
输出:2
示例 2:
输入:isConnected = [[1,0,0],[0,1,0],[0,0,1]]
输出:3
提示:
- 1 1 1 <= n <= 200 200 200
- n == isConnected.length
- n == isConnected[i].length
- isConnected[i][j] 为 1 1 1 或 0 0 0
- isConnected[i][i] == 1 1 1
- isConnected[i][j] == isConnected[j][i]
题解
方法一:DFS
思路
深度优先搜索的思路是很直观的。遍历所有城市,对于每个城市,如果该城市尚未被访问过,则从该城市开始深度优先搜索,通过矩阵 isConnected \textit{isConnected} isConnected 得到与该城市直接相连的城市有哪些,这些城市和该城市属于同一个连通分量,然后对这些城市继续深度优先搜索,直到同一个连通分量的所有城市都被访问到,即可得到一个省份。遍历完全部城市以后,即可得到连通分量的总数,即省份的总数。
代码实现
Leetcode 官方题解(递归):
class Solution {
public:
void dfs(vector<vector<int>>& isConnected, vector<int>& visited, int cities, int i) {
for (int j = 0; j < cities; j++) {
if (isConnected[i][j] == 1 && !visited[j]) {
visited[j] = 1;
dfs(isConnected, visited, cities, j);
}
}
}
int findCircleNum(vector<vector<int>>& isConnected) {
int cities = isConnected.size();
vector<int> visited(cities);
int provinces = 0;
for (int i = 0; i < cities; i++) {
if (!visited[i]) {
dfs(isConnected, visited, cities, i);
provinces++;
}
}
return provinces;
}
};
我自己的(迭代):
class Solution {
public:
int findCircleNum(vector<vector<int>>& isConnected) {
// 已知无向图的邻接矩阵,找出图中连通分量的个数
int size = isConnected.size(), ans = 0, city;
stack<int> tmp;
vector<bool> visited(size, false);
for(int n = 0; n < size; n++){
// 该城市尚未划分省份
if(visited[n] == false){
++ans;
tmp.push(n);
while(!tmp.empty()){
city = tmp.top();
tmp.pop();
if(visited[city] == true) continue;
visited[city] = true; // 划分省份
for(int i = 0; i < size; i++)
if(isConnected[city][i] == 1) tmp.push(i);
}
}
}
return ans;
}
};
复杂度分析
时间复杂度: O ( n 2 ) O(n^2) O(n2),其中 n n n 是城市的数量。需要遍历矩阵 isConnected \textit{isConnected} isConnected 中的每个元素。
空间复杂度: O ( n ) O(n) O(n),其中 n n n 是城市的数量。需要使用数组 visited \textit{visited} visited 记录每个城市是否被访问过,数组长度是 n n n,递归调用栈的深度不会超过 n n n。
方法二:BFS
思路
也可以通过广度优先搜索的方法得到省份的总数。对于每个城市,如果该城市尚未被访问过,则从该城市开始广度优先搜索,直到同一个连通分量中的所有城市都被访问到,即可得到一个省份。
代码实现
Leetcode 官方题解:
class Solution {
public:
int findCircleNum(vector<vector<int>>& isConnected) {
int cities = isConnected.size();
vector<int> visited(cities);
int provinces = 0;
queue<int> Q;
for (int i = 0; i < cities; i++) {
if (!visited[i]) {
Q.push(i);
while (!Q.empty()) {
int j = Q.front(); Q.pop();
visited[j] = 1;
for (int k = 0; k < cities; k++) {
if (isConnected[j][k] == 1 && !visited[k]) {
Q.push(k);
}
}
}
provinces++;
}
}
return provinces;
}
};
我自己的(迭代写法):
class Solution {
public:
int findCircleNum(vector<vector<int>>& isConnected) {
// 已知无向图的邻接矩阵,找出图中连通分量的个数
int size = isConnected.size(), ans = 0, city;
queue<int> tmp;
vector<bool> visited(size, false);
for(int n = 0; n < size; n++){
// 该城市尚未划分省份
if(visited[n] == false){
++ans;
tmp.push(n);
while(!tmp.empty()){
city = tmp.front();
tmp.pop();
if(visited[city] == true) continue;
visited[city] = true; // 划分省份
for(int i = 0; i < size; i++)
if(isConnected[city][i] == 1) tmp.push(i);
}
}
}
return ans;
}
};
复杂度分析
时间复杂度: O ( n 2 ) O(n^2) O(n2),其中 n n n 是城市的数量。需要遍历矩阵 isConnected \textit{isConnected} isConnected 中的每个元素。
空间复杂度: O ( n ) O(n) O(n),其中 n n n 是城市的数量。需要使用数组 visited \textit{visited} visited 记录每个城市是否被访问过,数组长度是 n n n,广度优先搜索使用的队列的元素个数不会超过 n n n。
方法三:并查集
思路
计算连通分量数的另一个方法是使用并查集。初始时,每个城市都属于不同的连通分量。遍历矩阵 isConnected \textit{isConnected} isConnected,如果两个城市之间有相连关系,则它们属于同一个连通分量,对它们进行合并。
遍历矩阵 isConnected \textit{isConnected} isConnected 的全部元素之后,计算连通分量的总数,即为省份的总数。
代码实现
Leetcode 官方题解:
class Solution {
public:
int Find(vector<int>& parent, int index) {
if (parent[index] != index) {
parent[index] = Find(parent, parent[index]);
}
return parent[index];
}
void Union(vector<int>& parent, int index1, int index2) {
parent[Find(parent, index1)] = Find(parent, index2);
}
int findCircleNum(vector<vector<int>>& isConnected) {
int cities = isConnected.size();
vector<int> parent(cities);
for (int i = 0; i < cities; i++) {
parent[i] = i;
}
for (int i = 0; i < cities; i++) {
for (int j = i + 1; j < cities; j++) {
if (isConnected[i][j] == 1) {
Union(parent, i, j);
}
}
}
int provinces = 0;
for (int i = 0; i < cities; i++) {
if (parent[i] == i) {
provinces++;
}
}
return provinces;
}
};
我自己的:
class Solution {
int Find(vector<int>& citys, int city){
if(citys[city] == city) return city;
else return citys[city] = Find(citys, citys[city]);
}
void Union(vector<int>& citys, int city1, int city2){
citys[Find(citys, city2)] = Find(citys, city1); // 将两个集合连接起来
}
public:
int findCircleNum(vector<vector<int>>& isConnected) {
// 已知无向图的邻接矩阵,找出图中连通分量的个数
int size = isConnected.size(), ans = 0, city, root1, root2;
vector<int> citys;
// 创建并查集数组
for(int n = 0; n < size; n++)
citys.push_back(n);
for(int n = 0; n < size; n++){
for(int i = 0; i < size; i++){
if(isConnected[n][i] == 1)
Union(citys, n, i);
}
}
for(int n = 0; n < size; n++)
if(citys[n] == n) ans++;
return ans;
}
};
复杂度分析
时间复杂度: O ( n 2 log n ) O(n^2 \log n) O(n2logn),其中 n n n 是城市的数量。需要遍历矩阵 isConnected \textit{isConnected} isConnected 中的所有元素,时间复杂度是 O ( n 2 ) O(n^2) O(n2),如果遇到相连关系,则需要进行 2 2 2 次查找和最多 1 1 1 次合并,一共需要进行 2 n 2 2n^2 2n2 次查找和最多 n 2 n^2 n2 次合并,因此总时间复杂度是 O ( 2 n 2 log n 2 ) = O ( n 2 log n ) O(2n^2 \log n^2)=O(n^2 \log n) O(2n2logn2)=O(n2logn)。这里的并查集使用了路径压缩,但是没有使用按秩合并,最坏情况下的时间复杂度是 O ( n 2 log n ) O(n^2 \log n) O(n2logn),平均情况下的时间复杂度依然是 O ( n 2 α ( n ) ) O(n^2 \alpha (n)) O(n2α(n)),其中 α \alpha α 为阿克曼函数的反函数, α ( n ) \alpha (n) α(n) 可以认为是一个很小的常数。
空间复杂度: O ( n ) O(n) O(n),其中 n n n 是城市的数量。需要使用数组 parent \textit{parent} parent 记录每个城市所属的连通分量的祖先。
边栏推荐
- 从外企离开,我才知道什么叫尊重跟合规…
- Uniapp uploads and displays avatars locally, and converts avatars into Base64 format and stores them in MySQL database
- AI super clear repair resurfaces the light in Huang Jiaju's eyes, Lecun boss's "deep learning" course survival report, beautiful paintings only need one line of code, AI's latest paper | showmeai info
- What is web penetration testing_ Infiltration practice
- TypeScript增量编译
- 如何判断一个数组中的元素包含一个对象的所有属性值
- Lombok 同时使⽤ @Data 和 @Builder 的坑,你中招没?
- Geo data mining (III) enrichment analysis of go and KEGG using David database
- GPIO简介
- Advanced learning of MySQL -- basics -- multi table query -- inner join
猜你喜欢
DAY THREE

stm32F407-------DAC数模转换

How can computers ensure data security in the quantum era? The United States announced four alternative encryption algorithms
Data analysis course notes (V) common statistical methods, data and spelling, index and composite index
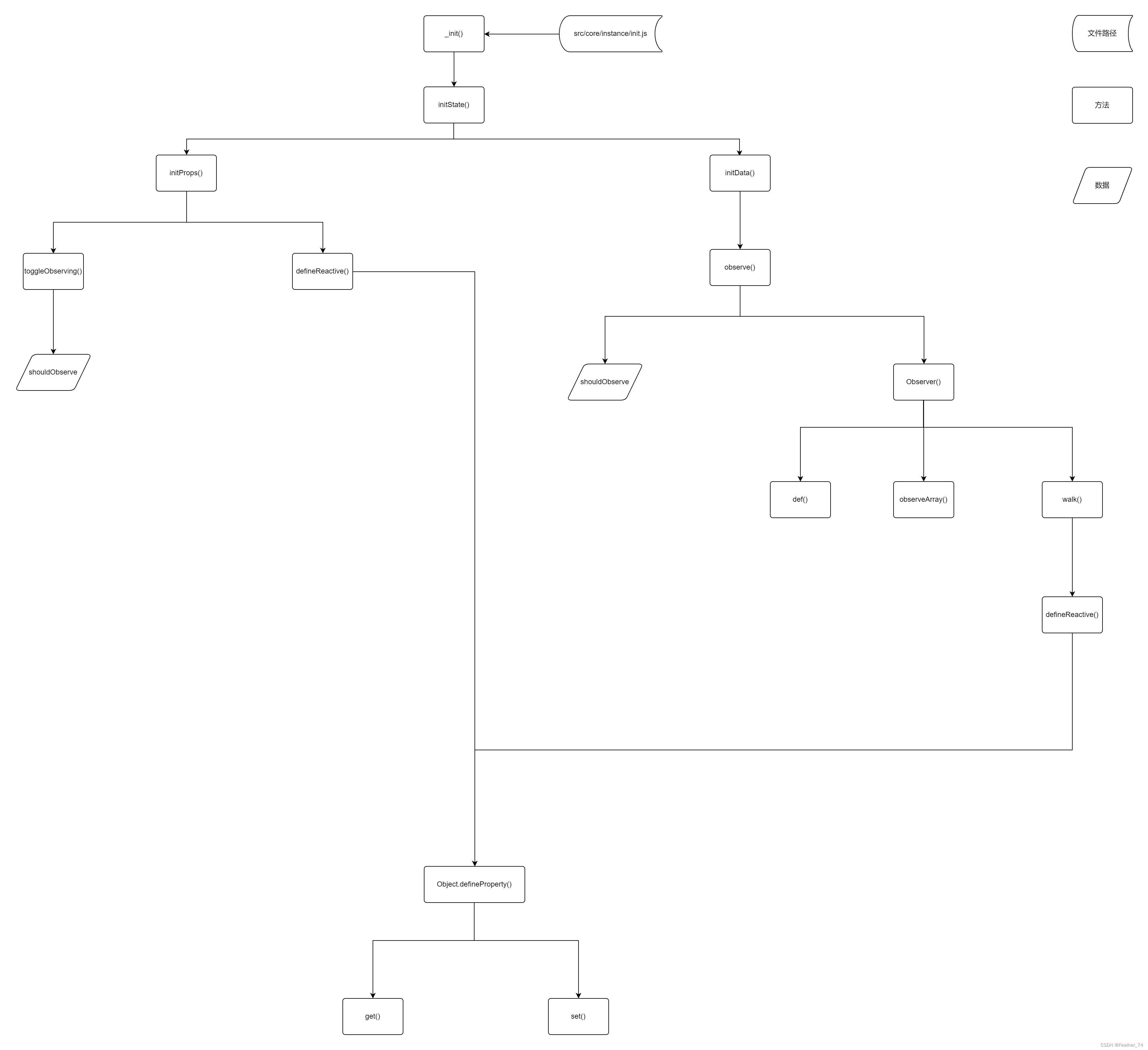
What is a responsive object? How to create a responsive object?
基于SSM框架的文章管理系统

Core knowledge of distributed cache

Mujoco second order simple pendulum modeling and control
The way of intelligent operation and maintenance application, bid farewell to the crisis of enterprise digital transformation
基於GO語言實現的X.509證書
随机推荐
Use source code compilation to install postgresql13.3 database
Data operation platform - data collection [easy to understand]
TypeScript增量编译
Uniapp uploads and displays avatars locally, and converts avatars into Base64 format and stores them in MySQL database
Three sentences to briefly introduce subnet mask
Use type aliases in typescript
2022/2/11 summary
Amazon MemoryDB for Redis 和 Amazon ElastiCache for Redis 的内存优化
基于SSM框架的文章管理系统
Command line kills window process
GPIO简介
How to set encoding in idea
Business process testing based on functional testing
Are you ready to automate continuous deployment in ci/cd?
Three application characteristics of immersive projection in offline display
如何判断一个数组中的元素包含一个对象的所有属性值
ldap创建公司组织、人员
How to use vector_ How to use vector pointer
Advanced learning of MySQL -- Fundamentals -- four characteristics of transactions
Leecode brush question record sword finger offer 58 - ii Rotate string left