当前位置:网站首页>2022/07/04学习记录
2022/07/04学习记录
2022-07-07 02:28:00 【a simple_boy】
简单的异或问题(构造 + 异或)
Description:
有一组整数 {0,1,2,…,2^m−1}, 请从中选出 k 个数,使得这 k 个数的异或和为 n, 请输出最大的满足条件的 k。
Solution:
既然要选择最多的k 那么我们可以想到0和x异或为x 我们让尽量多的数字异或和为0 最后找一个x
对 于 任 何 [ 0 , 2 m − 1 ] 中 , 举 例 0 ⊕ 7 = 1 ⊕ 6 = 2 ⊕ 5 = 3 ⊕ 4 = 0 那 么 总 异 或 和 就 为 0 所 以 如 果 我 们 需 要 一 个 数 n 的 话 , 我 们 就 会 将 带 有 n 的 数 对 拆 掉 , 且 去 掉 n 的 另 一 个 , 这 是 一 般 情 况 特 殊 情 况 就 是 当 n 和 m 特 别 小 的 时 候 我 们 需 要 分 类 讨 论 一 下 边 界 情 况 当 n = = 0 且 m ! = 1 的 时 候 , 我 们 可 以 一 个 都 不 去 掉 , k = 2 m 当 n = = 1 且 m = = 1 的 时 候 , k = 2 其 余 情 况 , 皆 为 正 常 情 况 , 有 k = 2 m − 1 对于任何[0, 2^m-1]中,举例0\oplus7 = 1\oplus6 = 2\oplus5 = 3\oplus4 = 0 \\那么总异或和就为0\\所以如果我们需要一个数n的话,我们就会将带有n的数对拆掉,且去掉n的另一个,这是一般情况\\特殊情况就是当n和m特别小的时候 我们需要分类讨论一下边界情况\\当n==0且m!=1的时候,我们可以一个都不去掉,k=2^m\\当n==1且m==1的时候,k=2\\其余情况,皆为正常情况,有k=2^m-1 对于任何[0,2m−1]中,举例0⊕7=1⊕6=2⊕5=3⊕4=0那么总异或和就为0所以如果我们需要一个数n的话,我们就会将带有n的数对拆掉,且去掉n的另一个,这是一般情况特殊情况就是当n和m特别小的时候我们需要分类讨论一下边界情况当n==0且m!=1的时候,我们可以一个都不去掉,k=2m当n==1且m==1的时候,k=2其余情况,皆为正常情况,有k=2m−1
Code:
int main()
{
cin >> n >> m;
LL res = (1LL << m);
if(n == 0 && m != 1)
cout << res << '\n';
else if(n == 1 && m == 1)
cout << 2 << '\n';
else
cout << res - 1LL << '\n';
}
完美数(构造 + 排列组合)
Description:
对于给定的数字 a , b ,当整数 n 在十进制下的所有数位都为 a 或 b 时,我们称 n 是“好数”
对于好数 n ,当 n 在十进制下每一位的数字之和也为“好数”时,我们称 n 是一个“完美数”
请你求出有多少 m 位数是“完美数”
(1≤m≤1e6,1≤a,b≤9)。
Solution:
由于m很大 你心想的dfs暴力行不通 O(2^m) 想来也是岂会那么简单
为什么dfs如此缓慢呢 因为对于每一位我都确认了他是a还是b 如果我避免这一点就可以节省大量时间
所以我们想到枚举a和b分别的数量 但是不考虑其摆放 花费时间O(n)
我们在枚举的同时 验证方案是否可行 大概是常数级别的时间
当方案可行的时候 我们要更新答案 如何更新呢 假设有x个a n-x个b 这是一种合法的方案
由于方案跟摆放顺序无关 于是这x个a可以放置在任意数位上 此时一个排列组合的做法就想到了
Code:
const int N = 1e6 + 5, mod = 1e9 + 7;
int a, b;
LL m;
LL fac[N], inv[N];
LL qmi(int a, int b)
{
LL res = 1;
while(b)
{
if(b & 1) res = res * a % mod;
a = a * 1LL * a % mod;
b >>= 1;
}
return res;
}
void init()
{
inv[0] = fac[0] = 1;
rep(i, 1, N)
fac[i] = i * fac[i - 1] % mod;
inv[N - 1] = qmi(fac[N - 1], mod - 2);
for(int i = N - 2; i; i --)
inv[i] = inv[i + 1] * (i + 1) % mod;
}
LL C(int a, int b)
{
return (fac[a] * inv[b] % mod * inv[a - b] % mod) % mod;
}
//组合数学板子
int main()
{
cin >> a >> b >> m;
init();
LL res = 0;
rep(i, 0, m + 1) //选i个b m-i个a 组合
{
LL last = m - i;
LL num = last * a + i * b;
bool flag = 1;
while(num)
{
if(num % 10 != a && num % 10 != b)
{
flag = false;
break;
}
num /= 10;
}
if(flag)
res = (res + C(m, i)) % mod;
}
cout << res;
}
数字组合(01背包求方案数)
Description:
给定 N 个正整数 A_1,A_2,…,A_N,从中选出若干个数,使它们的和为 M,求有多少种选择方案。
N < 100, M < 10000, A_i < 1000
Solution:
我们可以定义一个数组dp[ j ],表示和为j的方案数有多少种
显然dp[0] = 1
转移方程为dp[j] += dp[j - a[i]]
Code:
int main()
{
cin >> n >> m;
rep(i, 1, n + 1)
cin >> a[i];
dp[0] = 1;
rep(i, 1, n + 1)
for(int j = m; j >= a[i]; j --)
dp[j] += dp[j - a[i]];
cout << dp[m];
}
自然数拆分(完全背包求方案数)
Description:
给定一个自然数 N,要求把 N 拆分成若干个正整数相加的形式,参与加法运算的数可以重复。
- 拆分方案不考虑顺序;
- 至少拆分成 2 个数的和。
Solution:
这题还是求和的方案数,但是跟上一题的差别就在于上一题是每个数只能选一次 然而这一题每个数可以选任意次,所以这就是01背包和完全背包的区别了
定义数组dp[ j ] 表示和为j的方案数
dp[0] = 1
转移方程为dp[j] += dp[j - a[i]]
Code:
int main()
{
cin >> n;
dp[0] = 1;
for(int i = 1; i < n; i ++) //[1, n - 1]
for(int j = i; j <= n; j ++)
dp[j] = (dp[j] + dp[j - i]) % mod;
cout << dp[n];
}
记录一下区间DP板子题:合并石子
每次合并相邻两堆石子,合并代价为两堆石子的质量和,由于合并的顺序不同,因此付出的代价也就不同,请问合并长度为n的石子需要的最小代价是多少
N = 300
我们来了解一下区间DP的概念
区间DP是为了解决线性DP中分阶段划分问题时,与顺序相关和合并相关的问题而产生的
其主要的特点分为以下三点
- 合并:将两个或者多个部分进行整合,或者拆分
- 特征:将问题分解为两两合并的形式
- 求解:对整个问题设置最优值,枚举合并点,将问题分解为左右两个部分,最后通过合并两个部分的最优值来得到整个问题的最优值
对于本题而言 我们需要设置dp[ i ] [ j ]来表示和并[i, j]的最小代价
通过区间DP的特点 我们不难写出转移方程dp[ i ] [ j ] = min(dp[i] [k] + dp[k + 1] [j] + 合并需要付出的代价)
因为区间dp的性质 是将一个问题分为左右两个部分 于是我们必须先知道小的部分 才能向大的部分递推求解 这就决定了区间DP中的遍历顺序 也就是说我们必须先得到长度更小的区间的最优值 再向长度更大的区间递推而得最优值
//本题核心代码
memset(dp, 0x3f, sizeof dp);
for(int len = 1; len <= n; len ++)
{
for(int i = 1; i + len - 1 <= n; i ++)
{
int j = i + len - 1;
if(len == 1) //初始化为0
dp[i][j] = 0;
else //若len不为1 开始递推
{
for(int k = i; k < j; k ++)
dp[i][j] = min(dp[i][j], dp[i][k] + dp[k + 1][j] + s[j] - s[i - 1]); //s代表前缀和数组
}
}
}
//练习一下记忆化搜索写法
int dfs(int s, int e)
{
if(s == e) return 0;
int &v = dp[s][e];
if(v != -1) return v;
v = 1e9;
for(int k = s; k < e; k ++)
v = min(v, dfs(s, k) + dfs(k + 1, e) + pre_[e] - pre_[s - 1]);
return v;
}
明天一套CF 刷区间DP题目
边栏推荐
- matlab / ENVI 主成分分析实现及结果分析
- C language (structure) defines a user structure with the following fields:
- 如何解决数据库插入数据显示SQLSTATE[HY000]: General error: 1364 Field ‘xxxxx‘ doesn‘t have a default value错误
- 【luogu P1971】兔兔与蛋蛋游戏(二分图博弈)
- 软件测试到了35岁,真的就干不动了吗?
- string(讲解)
- Navicat导入15G数据报错 【2013 - Lost connection to MySQL server during query】 【1153:Got a packet bigger】
- 品牌电商如何逆势增长?在这里预见未来!
- Apache ab 压力测试
- 化工园区危化品企业安全风险智能化管控平台建设四大目标
猜你喜欢
力扣62 不同路径(从矩阵左上到右下的所有路径数量) (动态规划)
Several key steps of software testing, you need to know
SVN version management in use replacement release and connection reset
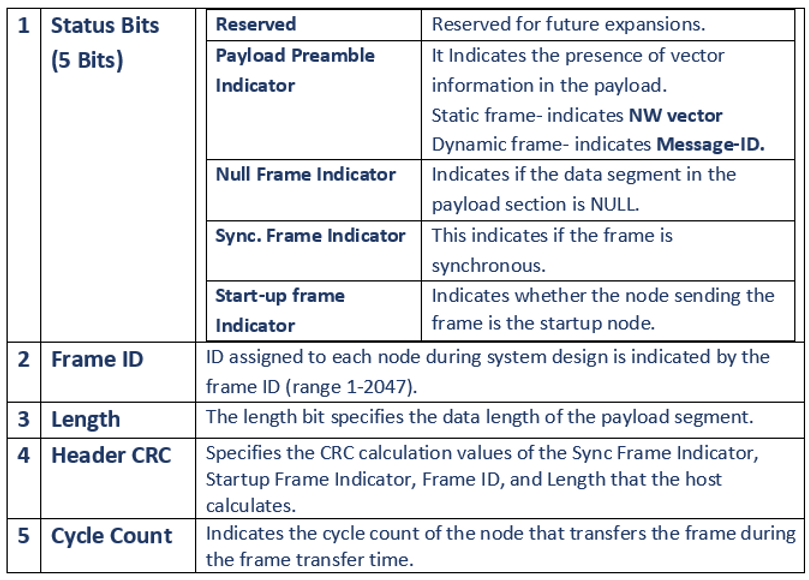
Overview of FlexRay communication protocol
Abnova 免疫组化服务解决方案
学习笔记|数据小白使用DataEase制作数据大屏
精准时空行程流调系统—基于UWB超高精度定位系统
MySQL installation

Which foreign language periodicals are famous in geology?
使用TCP/IP四层模型进行网络传输的基本流程
随机推荐
What are the classic database questions in the interview?
matlab / ENVI 主成分分析实现及结果分析
Haqi projection Black Horse posture, avec seulement six mois de forte pénétration du marché des projecteurs de 1000 yuans!
Stack and queue-p79-9
Wechat applet hides the progress bar component of the video tag
The difference between string constants and string objects when allocating memory
POI导出Excel:设置字体、颜色、行高自适应、列宽自适应、锁住单元格、合并单元格...
How can I check the DOI number of a foreign document?
LM11丨重构K线构建择时交易策略
Kotlin之 Databinding 异常
学习笔记|数据小白使用DataEase制作数据大屏
docker-compose启动redis集群
使用net core优势/为什么使用
JESD204B时钟网络
力扣62 不同路径(从矩阵左上到右下的所有路径数量) (动态规划)
Ha Qu projection dark horse posture, only half a year to break through the 1000 yuan projector market!
屏幕程序用串口无法调试情况
SVN version management in use replacement release and connection reset
MySQL卸载文档-Windows版
String (explanation)
