当前位置:网站首页>求组合数 AcWing 887. 求组合数 III
求组合数 AcWing 887. 求组合数 III
2022-07-05 06:16:00 【T_Y_F666】
求组合数 AcWing 887. 求组合数 III
原题链接
算法标签
组合数学 组合计数 Lucas定理 逆元 快速幂 费马小定理
思路

代码
#include<bits/stdc++.h>
#define int long long
#define abs fabs
#define rep(i, a, b) for(int i=a;i<b;++i)
#define Rep(i, a, b) for(int i=a;i>=b;--i)
using namespace std;
const int N = 105;
double a[N][N], eps = 1e-8;
int n;
inline int read(){
int s=0,w=1;
char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
return s*w;
}
void put(int x) {
if(x<0) putchar('-'),x=-x;
if(x>=10) put(x/10);
putchar(x%10^48);
}
int qmi(int a, int b, int p){
int ans=1;
while(b){
if(b&1){
ans=ans*a%p;
}
a=a*a%p;
b>>=1;
}
return ans;
}
int C(int a, int b, int p){
if(a<b){
return 0;
}else{
int res=1;
// for循环只执行了b次,所以是从a开始乘了b个数,即a*(a-1)*…*(a-b+1),也就等于a!/(a-b)!
for(int i=1, j=a; i<=b; ++i, --j){
res=res*j%p;
res=res*qmi(i, p-2, p)%p;
}
return res;
}
}
int lu(int a, int b, int p){
if(a<p&&b<p){
return C(a, b, p);
}else{
return C(a%p, b%p, p)*lu(a/p, b/p, p)%p;
}
}
signed main(){
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
n=read();
while(n--){
int a=read(), b=read(), p=read();
printf("%lld\n", lu(a, b, p));
}
}
原创不易
转载请标明出处
如果对你有所帮助 别忘啦点赞支持哈
边栏推荐
- 4. 对象映射 - Mapping.Mapster
- C - XOR to all (binary topic)
- Leetcode-1200: minimum absolute difference
- 【LeetCode】Easy | 20. Valid parentheses
- A reason that is easy to be ignored when the printer is offline
- [BMZCTF-pwn] ectf-2014 seddit
- Record the process of configuring nccl and horovod in these two days (original)
- One question per day 1020 Number of enclaves
- 4. Object mapping Mapster
- 实时时钟 (RTC)
猜你喜欢

阿里新成员「瓴羊」正式亮相,由阿里副总裁朋新宇带队,集结多个核心部门技术团队
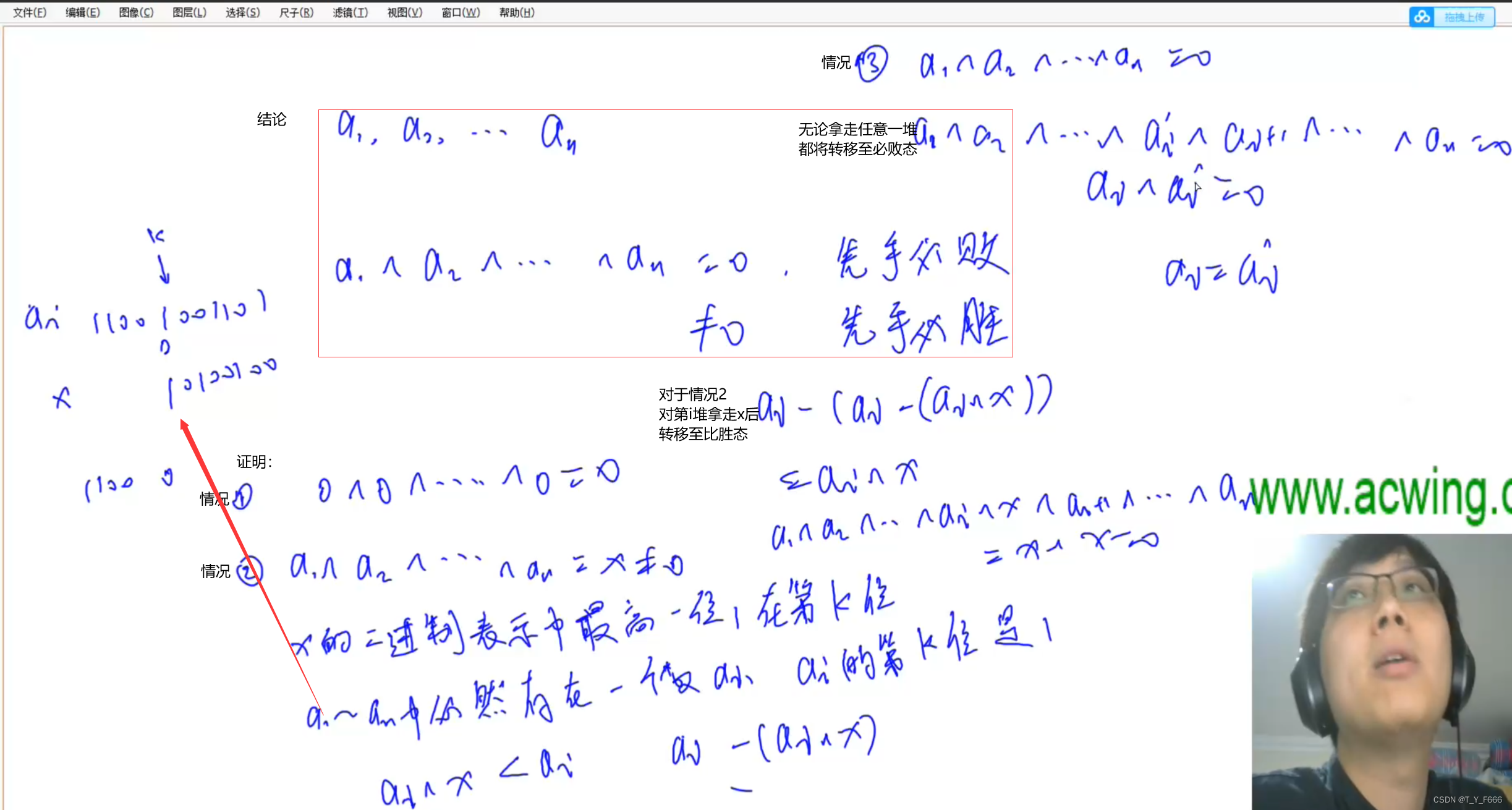
博弈论 AcWing 891. Nim游戏
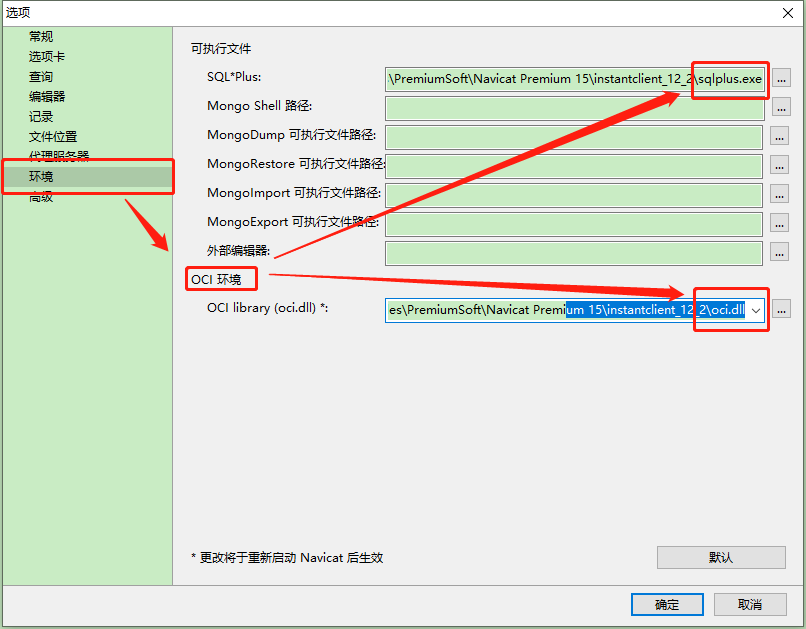
Error ora-28547 or ora-03135 when Navicat connects to Oracle Database

博弈论 AcWing 894. 拆分-Nim游戏

Operator priority, one catch, no doubt
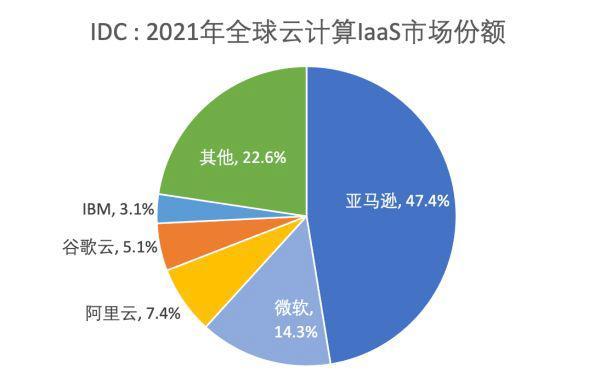
快速使用Amazon MemoryDB并构建你专属的Redis内存数据库
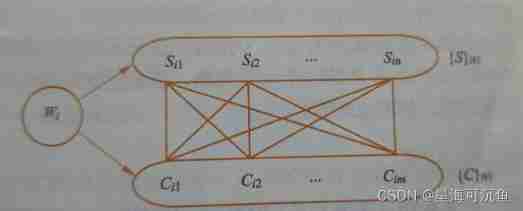
Chapter 6 relational database theory
QQ电脑版取消转义符输入表情

背包问题 AcWing 9. 分组背包问题

redis发布订阅命令行实现
随机推荐
Presentation of attribute value of an item
2021apmcm post game Summary - edge detection
Sqlmap tutorial (II) practical skills I
SPI details
Chapter 6 relational database theory
数据可视化图表总结(二)
MySQL advanced part 1: index
阿里巴巴成立企业数智服务公司“瓴羊”,聚焦企业数字化增长
leetcode-6110:网格图中递增路径的数目
Leetcode-6109: number of people who know secrets
Real time clock (RTC)
Leetcode-1200: minimum absolute difference
Leetcode backtracking method
【Rust 笔记】17-并发(下)
Currently clicked button and current mouse coordinates in QT judgment interface
Niu Mei's math problems
Leetcode-9: palindromes
How to understand the definition of sequence limit?
11-gorm-v2-02-create data
中国剩余定理 AcWing 204. 表达整数的奇怪方式