当前位置:网站首页>【LeetCode】Day95-有效的数独&矩阵置零
【LeetCode】Day95-有效的数独&矩阵置零
2022-07-05 06:13:00 【倒过来是圈圈】
题目1
题解
如果按照规则行、列、3*3矩阵挨个试的话,工作量巨大…所以怎么才能降低复杂度呢?是这道题要重点考虑的问题
可以使用哈希表记录每一行、每一列和每一个小九宫格中,每个数字出现的次数。只需要遍历数独一次,在遍历的过程中更新哈希表中的计数,并判断是否满足有效的数独的条件即可。
class Solution {
public boolean isValidSudoku(char[][] board) {
int rows[][]=new int[9][9];//行
int columns[][]=new int[9][9];//列
int three[][][]=new int[3][3][9];//小九宫格
for(int i=0;i<9;i++){
for(int j=0;j<9;j++){
if(board[i][j]!='.'){
int index=board[i][j]-'0'-1;//字符转换为数字
rows[i][index]++;
columns[index][j]++;
three[i/3][j/3][index]++;//注意怎么表示小九宫格的哈希表
if(rows[i][index]>1||columns[index][j]>1||three[i/3][j/3][index]>1)
return false;
}
}
}
return true;
}
}
时间复杂度: O ( 1 ) O(1) O(1),数独大小是固定的,因此复杂度为O(1)
空间复杂度: O ( 1 ) O(1) O(1),由于数独大小固定,因此哈希表大小也固定,复杂度为O(1)
题目2
题解
使用两个数组row[]和column[]标记哪行哪列有0
class Solution {
public void setZeroes(int[][] matrix) {
int m=matrix.length,n=matrix[0].length;
boolean[] row=new boolean[m];
boolean[] column=new boolean[n];
for(int i=0;i<m;i++){
for(int j=0;j<n;j++){
//元素为0,行列打标记
if(matrix[i][j]==0){
row[i]=true;
column[j]=true;
}
}
}
//根据标记,行列赋零
for(int i=0;i<m;i++){
for(int j=0;j<n;j++){
if(row[i]==true||column[j]==true)
matrix[i][j]=0;
}
}
}
}
时间复杂度: O ( m n ) O(mn) O(mn)
空间复杂度: O ( m + n ) O(m+n) O(m+n)
边栏推荐
- Data visualization chart summary (I)
- “磐云杯”中职网络安全技能大赛A模块新题
- Binary search template
- Leetcode-31: next spread
- Sqlmap tutorial (II) practical skills I
- leetcode-556:下一个更大元素 III
- Groupbykey() and reducebykey() and combinebykey() in spark
- Introduction and experience of wazuh open source host security solution
- leetcode-9:回文数
- 多屏电脑截屏会把多屏连着截下来,而不是只截当前屏
猜你喜欢

1.15 - input and output system
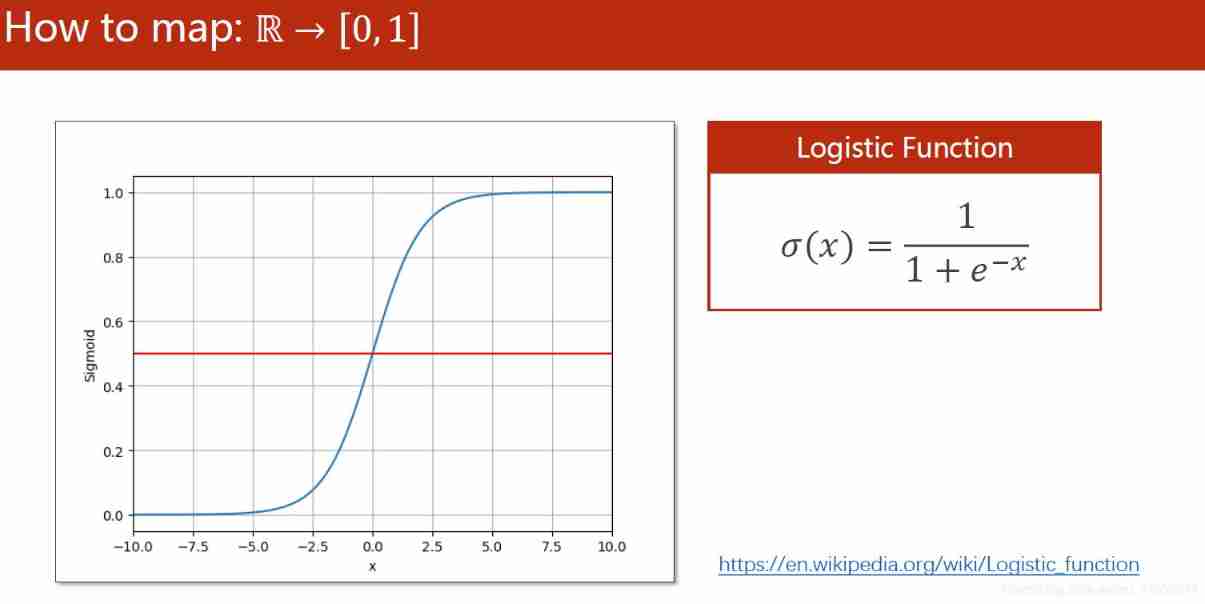
6. Logistic model
Appium自动化测试基础 — Appium测试环境搭建总结
QQ computer version cancels escape character input expression
WordPress switches the page, and the domain name changes back to the IP address
Error ora-28547 or ora-03135 when Navicat connects to Oracle Database
Leetcode-6108: decrypt messages

Navicat連接Oracle數據庫報錯ORA-28547或ORA-03135

数据可视化图表总结(二)

Arduino 控制的 RGB LED 无限镜
随机推荐
Individual game 12
Implement a fixed capacity stack
Time of process
leetcode-22:括号生成
2022年贵州省职业院校技能大赛中职组网络安全赛项规程
redis发布订阅命令行实现
leetcode-31:下一个排列
Data visualization chart summary (II)
Leetcode-3: Longest substring without repeated characters
SQLMAP使用教程(二)实战技巧一
“磐云杯”中职网络安全技能大赛A模块新题
[rust notes] 15 string and text (Part 1)
Arduino 控制的 RGB LED 无限镜
SPI 详解
Quickly use Amazon memorydb and build your own redis memory database
MIT-6874-Deep Learning in the Life Sciences Week 7
Sword finger offer II 058: schedule
[practical skills] how to do a good job in technical training?
WordPress switches the page, and the domain name changes back to the IP address
Control unit