当前位置:网站首页>Xcit learning notes
Xcit learning notes
2022-07-07 08:21:00 【Fried dough twist ground】
XCiT Learning notes
XCiT: Cross-Covariance Image Transformers
Abstract
After the great success of natural language processing ,transformers Recently, it has shown great prospects in computer vision .transformers The underlying self attention operation generates all tokens ( That is, text or image block ) Global interaction between , It also allows flexible modeling of image data beyond the local interaction of convolution . However , This flexibility has secondary complexity in terms of time and memory , It hinders the application of long sequence and high-resolution images . We put forward a kind of “transposed” Self attention of version , It operates across feature channels rather than tokens , The interaction is based on the cross covariance matrix between the key and the query . The resulting cross-covariance attention(XCA) It has linear complexity in the number of tokens , And allows efficient processing of high-resolution images . Our cross covariance image converter (XCiT) be based on XCA structure , Combine the accuracy of traditional converter with the scalability of convolution architecture . We verify this by reporting excellent results on multiple visual benchmarks XCiT Effectiveness and generality of , Included in ImageNet-1k Upper ( Self supervision ) Image classification 、 stay COCO Object detection and instance segmentation on and on ADE20k Semantic segmentation on . The code is published in :https://github.com/facebookresearch/xcit
1 Introduction
Transformers framework [69] In speech and natural language processing (NLP) Has achieved quantitative and qualitative breakthroughs . lately ,Dosovitskiy wait forsomeone [22] take transformers Establish a feasible framework for learning visual representation , Report the competitive results of image classification , At the same time, rely on large-scale pre training .Touvron wait forsomeone [65] indicate , When extensive data enhancement and improved training programs are used ImageNet-1k When training transformer , With strong convolution baseline ( Such as efficiency net [58]) comparison , precision / Throughput is equal to or better . For other visual tasks , Including image retrieval [23]、 Object detection and semantic segmentation [44、71、81、83] And video understanding [2、7、24], Good results have been achieved .
transformers One of the main disadvantages of is the time and memory complexity of the core self attention operation , As the number of input tokens or similar patches in computer vision increases, it increases twice . about w×h Images , This translates into O ( w 2 h 2 ) O(w^2h^2) O(w2h2) Complexity , This is forbidden for most tasks involving high-resolution images , For example, object detection and segmentation . Various strategies have been proposed to alleviate this complexity , For example, using Approximate form of self attention [44,81], or Gradually reduce the pyramid structure of feature map sampling [71]. However , None of the existing solutions is completely satisfactory , Because they either trade complexity for accuracy , Or its complexity is still too high for processing large images .
We will Vaswani wait forsomeone [69] The self attention initially introduced is replaced by “ Transposition ” attention , We express it as “cross-covariance attention”(XCA). Cross covariance attention replaces the explicit pairwise interaction between tokens by self attention between features , Note that the graph is derived from the cross covariance matrix calculated on the key and query projection of the token feature . It is important to ,XCA Linear complexity in the number of patches . In order to construct a cross covariance image converter (XCiT), We will XCA Combined with local patch interaction module , These modules rely on effective depth convolution and point feedforward networks commonly used in converters , See the picture 1.XCA Can be considered dynamic 1×1 A form of convolution , This convolution multiplies all tokens by the same data correlation weight matrix . We found that , our XCA The performance of layer can be further improved by applying it to channel blocks rather than directly mixing all channels together .XCA This kind of “ Block diagonally ” Shape further reduces the computational complexity , The factor in the number of blocks is linear .
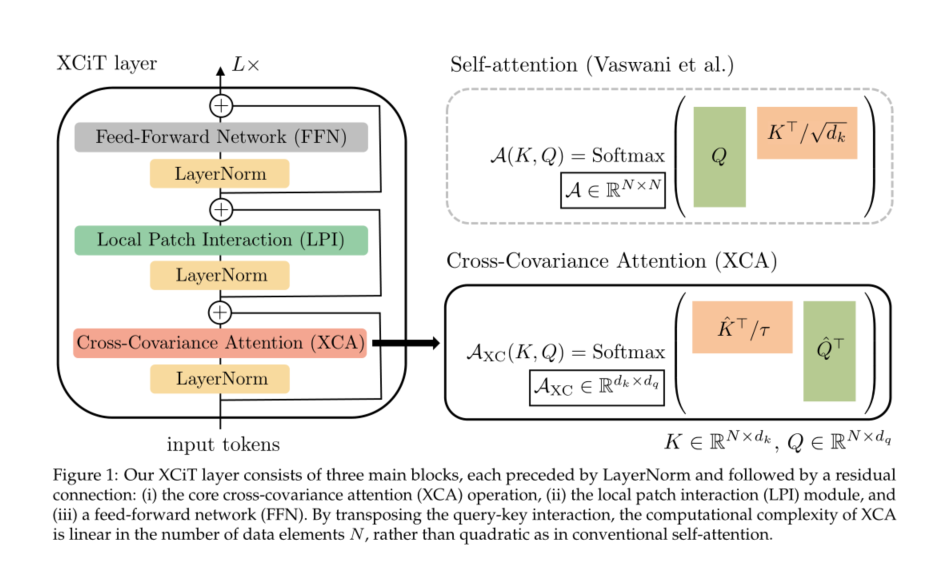
Given the linear complexity of the number of tokens **,XCiT It can effectively deal with more than 1000 Pixel image **. It is worth noting that , Our experiments show that ,XCiT Will not affect the accuracy , And under similar settings, we get DeiT[65] and CaiT[68] Similar results . Besides , For intensive forecasting tasks , Such as object detection and image segmentation , Our model is superior to the popular ResNet[28] Backbone and recently based on transformer Model of [44、71、81]. Last , We have also succeeded in XCiT Apply to use DINO[12] Self supervised feature learning , And it is proved that DeiT The backbone of [65] Compared with the performance .
in general , Our contributions are summarized as follows :
1) We introduce cross covariance attention (XCA), It provides traditional self attention “ Transposition ” Alternatives , adopt Channels rather than tokens participate . Its complexity is linear in the number of tokens , Allows efficient processing of high-resolution images , See the picture 2.
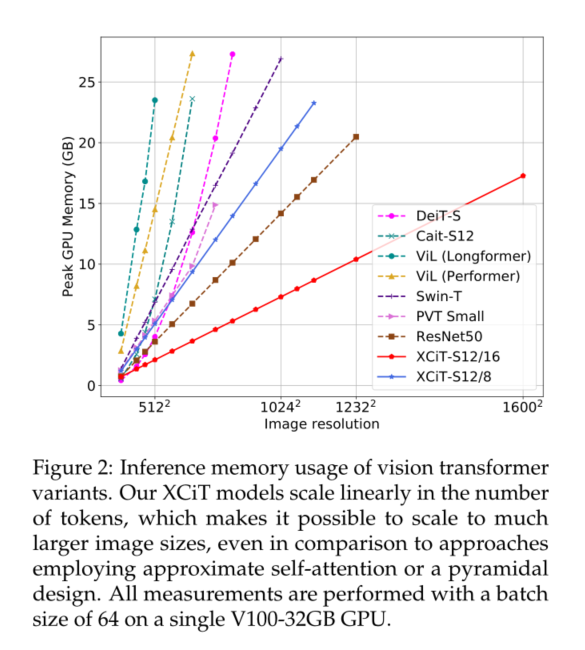
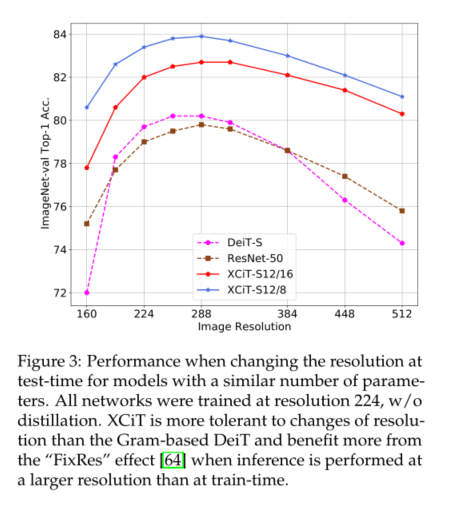
2)XCA Focus on a fixed number of channels , It has nothing to do with the number of tokens . therefore , Our model is more robust to changes in image resolution during testing , Therefore, it is more suitable for processing variable size images .
3) For image classification , We prove , about Multiple model sizes using simple columnar structures , Our model is equivalent to the most advanced visual converter , namely , We keep the resolution constant between layers . especially , our XCiT-L24 Model in ImageNet It has been realized. 86.0% Of top-1 precision , Better than the equivalent number of parameters CaiT-M24[68] and NFNet-F2[10].
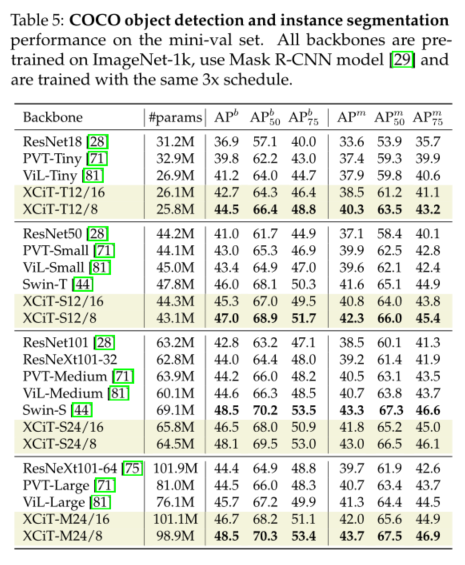
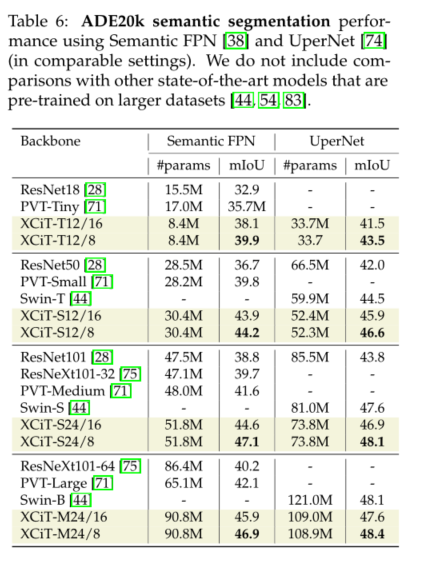
4) For dense prediction tasks with high-resolution images , Our model is superior to ResNet And multi transformer based backbone . stay COCO On the benchmark , We have achieved 48.5% and 43.7% Object detection and instance segmentation . Besides , We are ADE20k Reported on the benchmark 48.4% Of mIoU For semantic segmentation , It is superior to the most advanced in all comparable model sizes Swin Transformer[44] The trunk .
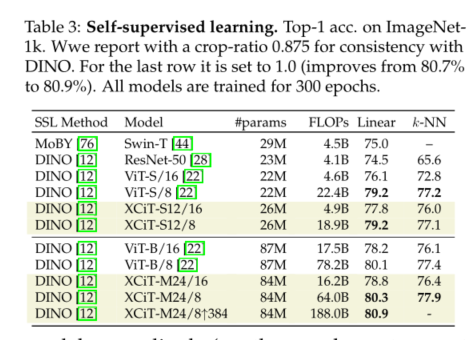
5) Last , our XCiT The model is very effective in self supervised learning settings , Use DINO[12] stay ImageNet-1k It has been realized. 80.9% Of top-1 precision .
2 Related work
Deep vision transformers.
Due to instability and optimization problems , Training depth vision converters can be challenging .Touvron wait forsomeone [68] Use layered scale (LayerScale) Successfully trained up to 48 Layer model , This ratio measures the contribution of the remaining blocks of each layer , And improved optimization . Besides , The author introduces the class attention layer , Decouple the learning of patch features from the feature aggregation stage of classification .
Spatial structure in vision transformers.
Yuan et al [79] Soft segmentation is applied to patch projection with overlapping patches , The patch is applied repeatedly on the model layer , Gradually reduce the number of patches . Han et al [27] The converter module for on-chip structure is introduced 2, Utilize pixel level information and integrate with inter chip converter to obtain higher representation capability .d’Ascoli wait forsomeone [19] The initialization of self attention block is regarded as convolution operator , It is proved that this initialization improves the performance of the visual converter in low data state .Graham wait forsomeone [26] It introduces LeViT, It adopts a multi-level architecture , Similar to the popular convolution architecture , With gradually decreasing feature resolution , Allow the model to have high reasoning speed , While maintaining strong performance . Besides , The author uses a convolution based module to extract the patch descriptor . Yuan et al [78] By replacing linear patch projection with convolution layer and maximum pool , And modifying the feedforward network in each transform layer to merge the depth convolution , The performance and convergence speed of the visual converter are improved .
Efficient attention
In order to solve the secondary complexity of self attention in the number of input tokens , Many effective self attention methods have been proposed in the literature . These include limiting the scope of self attention to local windows [48,50]、 Step mode [14]、 Axial mode [30] Or cross layer adaptive computing [57]. Other methods provide an approximation of the self attention matrix , You can mark the projection on the dimension [70] Or through softmax Factorization of attention nuclei [15、37、56、77] To achieve , This avoids explicit computation of the attention matrix . Although conceptually different , our XCA Perform similar calculations , But not sensitive to the choice of kernel . Again ,Lee Thorp wait forsomeone [41] Faster training is achieved by replacing self attention with nonparametric Fourier transform . Other effective attention methods rely on local attention and add a small number of global tokens , Therefore, the interaction between all tokens is allowed only by jumping the global token [1、5、34、80].
Transformers for high-resolution images.
Some works use visual converters to complete high-resolution image tasks other than image classification , Such as object detection and image segmentation . Wang et al [71] A model with pyramid structure is designed , And solve the complexity by gradually reducing the spatial resolution of keys and values . Similarly , For video recognition ,Fan wait forsomeone [24] Use the pool to reduce the resolution across the space-time dimension , To allow effective calculation of the attention matrix .Zhang wait forsomeone [81] Adopt global token and local attention to reduce the complexity of the model , and Liu wait forsomeone [44] It provides an effective method of local attention using moving windows . Besides ,Zheng wait forsomeone [83] and Ranftl wait forsomeone [54] The semantic segmentation and monocular depth estimation of secondary self attention operation are studied .
Data-dependent layers
our XCiT The layer can be regarded as a “ dynamic ”1×1 Convolution , It multiplies all token characteristics by the same data correlation weight matrix , The matrix is derived from the key and query cross covariance matrix . In the context of convolutional Networks , Dynamic filter network [9] Explored a related idea , That is, a filter generation sub network is used to generate a convolution filter based on the features in the previous layer .**Squeeze-and-Excitation The Internet [32] Use data related in convolution structures 1×1 Convolution . The spatial average pool feature is fed to 2 layer MLP, The MLP Generate scaling parameters per channel .** Closer to our work in spirit ,Lambda layers Proposed a way to ensure ResNet The method of global interaction in the model [4]. their “ Content based lambda function ” The calculated term is similar to our cross covariance note , But in the application softmax and ’2 Normalization is different . Besides ,Lambda The layer also includes specific location-based Lambda function ,LambdaNetworks be based on resnet, and XCiT follow ViT framework . Recently, we also found that , Data independent self attention analogues are effective substitutes for visual task convolution layer and self attention layer [21、46、63、67]. These methods visualize the bars in the attention map as learnable parameters , Instead of dynamically deriving attention maps from queries and keys , But its complexity is still secondary in the number of tokens . Zhao et al [82] Alternative forms of attention in computer vision are considered .
3 Method
In this section , We first review the self attention mechanism , as well as Gram The relationship between matrix and covariance matrix , This inspired our work . then , We propose a cross covariance attention operation (XCA)—— This operation operates along the feature dimension rather than the token dimension in the traditional converter —— It is combined with local patch interaction and feedforward layer to construct cross covariance image converter (XCiT). See Fig 1 For an overview
3.1 Background
Token self-attention.
Vaswani wait forsomeone [69] The self attention introduced acts on the input matrix X ∈ R N × d X∈ R^{N×d} X∈RN×d, among N Is the number of tokens , The dimension of each token is d. Input X Use the weight matrix W q ∈ R d × d q , W k ∈ R d × d k and W v ∈ R d × d v W_q∈ R^{d×d_q},W_k∈ R^{d×d_k} and W_v∈ R^{d×d_v} Wq∈Rd×dq,Wk∈Rd×dk and Wv∈Rd×dv Linear projection to query 、 Key and value , bring Q = X W q , K = X W k , V = X W v Q=XW_q,K=XW_k,V=XW_v Q=XWq,K=XWk,V=XWv, among d q = d k d_q=d_k dq=dk. Keys and values are used to calculate the attention map A ( K , Q ) = S o f t m a x ( Q K > / √ d k ) A(K,Q)=Softmax(QK>/√d_k) A(K,Q)=Softmax(QK>/√dk), And the output of self attention operation is defined as V in N Weighted sum of token characteristics , Its weight corresponds to attention mapping : A t t e n t i o n ( Q , K , V ) = A ( K , Q ) V Attention(Q,K,V)=A(K,Q)V Attention(Q,K,V)=A(K,Q)V. Because of all N Pairwise interaction between elements , The computational complexity of self attention is N Zoom twice in .
Relationship between Gram and covariance matrices
In order to stimulate our cross covariance, pay attention to the operation , We recall Gram And covariance matrix . Informal d×d The covariance matrix is C = X T X C=X^TX C=XTX Obtained at .N×N Gram The matrix contains all pairwise inner products : G = X X T G=XX^T G=XXT.Gram It is equivalent to the non-zero part of the characteristic spectrum of the covariance matrix , And can calculate each other C and G Eigenvector of . If V yes G Eigenvector of , be C The eigenvector of is determined by U=XV give . To minimize computing costs , It can be obtained from the decomposition of another matrix Gram Characteristic decomposition of matrix or covariance matrix , It depends on which of the two matrices is the smallest .
We make use of Gram And covariance matrix to consider whether it is possible to avoid calculation N×N Notice the quadratic cost of the matrix , Note that the matrix is from N×N Gram matrix Q K T = X W q W k T X T QK^T=XW_qW_k^{T}X^{T} QKT=XWqWkTXT Simulated by . Now let's consider how to use dk×dq Cross covariance matrix , K T Q = W k T X T X W q K^TQ=W_k^{T}X^TXW_q KTQ=WkTXTXWq, The matrix can be expressed in the number of elements in linear time N Calculation , To define the attention mechanism .
3.2 Cross-covariance attention
We propose a self attention function based on cross covariance , This function runs along the feature dimension , Instead of running along the token dimension like token self attention . Use the above query 、 Definition of keys and values , The cross covariance attention function is defined as :
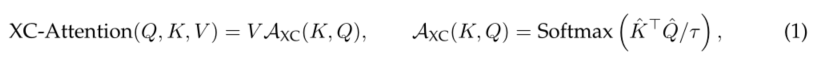
among , Each output token is embedded in its corresponding token V Medium dv Convex combination of features . Attention weight A Based on the cross covariance matrix .
L2-Normalization and temperature scaling.
In addition to constructing attention operations on the cross covariance matrix , We also modified the token self attention for the second time . We go through "L2- Regularization ” To limit the size of query matrix and key matrix , Make the normalized matrix Q ^ \hat{Q} Q^ and K ^ \hat{K} K^ The length of N Each column of has a unit norm , also d×d Cross covariance matrix $ \hat{K}^{\top} \hat{Q}$ Every element in is in scope [−1, 1]. We observed that , Controlling norms can significantly enhance the stability of training , Especially when training with a variable number of tokens . However , Limiting specifications reduces the power of representativeness by removing degrees of freedom . therefore , We introduce a learnable temperature parameter τ, The parameter is in Softmax Before scaling the inner product , Allow the distribution of attention weights to be clearer or more uniform .
Block-diagonal cross-covariance attention.
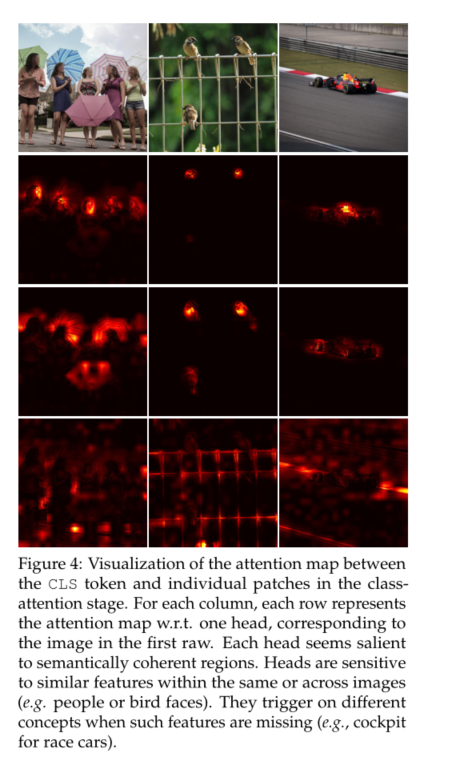
We don't allow all features to interact , Instead, divide them into h Group , or “ head ”, In a way similar to the way that bulls mark their attention . We apply cross covariance attention to each head separately , For each head , Let's learn the individual weight matrix , take X Project to query 、 Key and value , And in tensor W q ∈ R h × d × d q , W k ∈ R h × d × d k and W v ∈ R h × d × d v W_q∈ R^{h×d×d_q},W_k∈ R^{h×d×d_k} and W_v∈R^{h×d×d_v} Wq∈Rh×d×dq,Wk∈Rh×d×dk and Wv∈Rh×d×dv Collect the corresponding weight matrix , Among them, we set d k = d q = d v = d / h d_k=d_q=d_v=d/h dk=dq=dv=d/h. Limiting attention in the head has two advantages :(i) use The complexity of the aggregated value of attention weight is reduced by a factor h;(ii) what's more , We have observed from experience that , The block diagonal version is easier to optimize , And usually the reasons for improving the results . This observation is consistent with Group Normalization[73] The observations are consistent ,Group Normalization The channel groups are normalized according to the statistical data of the channel groups , And merge all channels into a single group Layer Normalization[3] comparison , Good results have been achieved for computer vision tasks . chart 4 Show , Each head learns to focus on the semantic coherence of the image , At the same time, it can flexibly change the feature type it focuses on according to the image content .
Complexity analysis.
Usual h The time complexity of head marking self attention is O ( N 2 D ) O(N^2D) O(N2D), The space complexity is O ( h N 2 + N d ) O(hN^ 2+Nd) O(hN2+Nd). Due to quadratic complexity , It is problematic to extend the self attention of tokens to images with a large number of tokens . Our cross covariance attention overcomes this shortcoming , Because of its calculation cost O ( N d 2 / h ) O(Nd^2/h) O(Nd2/h) Linearly proportional to the number of tokens , as well as O ( d 2 / h + N d ) O(d^2/h+Nd) O(d2/h+Nd) Memory complexity . therefore , Our model can be better extended to the number of tokens N more 、 Characteristic dimension d Relatively small case , This is a typical case , Especially when splitting features into h At the beginning .
3.3 Cross-covariance image transformers
In order to construct a cross covariance image converter (XCiT), We use a columnar structure , The structure maintains the same spatial resolution between layers , Be similar to [22、65、68]. We will pay attention to the cross covariance (XCA) Block is combined with the following add-on modules , There is one in front of each module LayerNorm[3]. See Fig 1 For an overview . Because in this section , We designed models specifically for computer vision tasks , Therefore, the token corresponds to the image patch in this context .
Local patch interaction.
stay XCA In block , The communication between patches is only implicit by sharing statistical information . To achieve explicit communication across patches , We are in each XCA A simple local patch interaction is added after the block (LPI) block .**LPI By two depth directions 3×3 The convolution layer consists of , There are batch normalization and GELU nonlinear .** Because of its depth structure ,LPI The cost of the block in terms of parameters is negligible , The overhead in terms of throughput and memory usage during reasoning is very limited .
Feed-forward network.
As is common in Transformer Models , We add a point by point feedforward network (FFN), The network has a network with 4d Hidden layers of hidden cells . Although the interaction between features is limited to XCA Within the group in the block , also LPI There is no feature interaction in the block , but FFN Allow interaction between all features .
Global aggregation with class attention
When training our image classification model , We used Touvron wait forsomeone [68] Proposed Class attention layer . These layers pass CLS One way note writing between token and patch embedding CLS Token to aggregate the last XCiT Layer patch embedding . Classified attention also applies to each head , Feature group .
Handling images of varying resolution.
Different from the attention map involved in token self attention , In our case , Covariance block size is fixed , It has nothing to do with the resolution of the input image .softmax Always run on the same number of elements , This can explain why our model performs better when dealing with images with different resolutions ( See the picture 3). stay XCiT in **, We include additive sine position coding with input tokens [69]**. We from 2d Patch coordinates are in 64 To sustain them , Then, it is linearly projected to the working dimension of the transformer . This choice is orthogonal to the use of learning location coding , Such as ViT[22]. However , It is more flexible , Because there is no need to interpolate or fine tune the network when changing the image size .
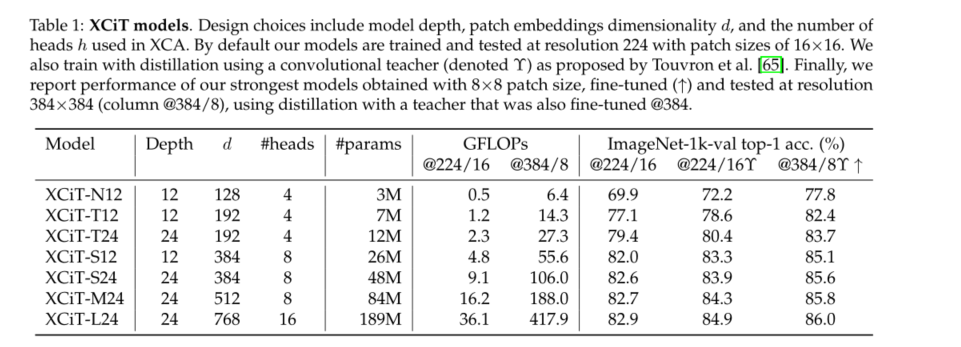
Model configurations.
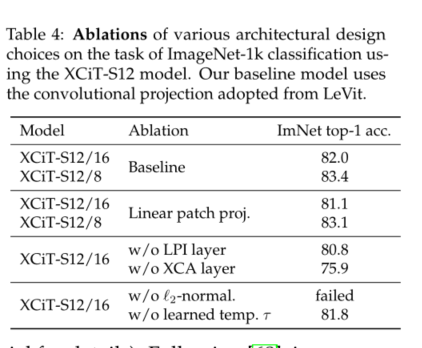
In the table 1 in , We listed different variants of the model we used in the experiment , There are different choices for the width and depth of the model . For patch coding layer , Unless otherwise stated , Otherwise we adopt Graham wait forsomeone [26] Use the convolution patch projection layer alternative . We also tested [22] Linear patch projection described in , See table 4 Melting in . Our default patch size is 16×16, Like other visual converter models , Include ViT[22]、DeiT[65] and CaiT[68]. We also treat smaller 8×8 The patch was tested , It is observed that this patch can improve performance [12]. Be careful , This is for XCiT It works , Because its complexity is linearly proportional to the number of patches , and ViT、DeiT and CaiT It becomes a quadratic proportion
4 Experimental evaluation
5 Conclusion
We propose an alternative method of token self attention that operates on the feature dimension , It eliminates the need for expensive calculation of secondary attention mapping . We establish a cross covariance attention centered XCiT Model , It also proves the effectiveness and versatility of our model in various computer vision tasks . especially , It shows up with the most advanced transformer The model has quite strong image classification performance , At the same time, the change of image resolution also has ConvNet Similar robustness .XCiT It is an effective backbone for intensive prediction tasks , In object detection 、 Excellent performance in instance and semantic segmentation . Last , We proved that XCiT It can become a strong pillar of self supervised learning , Match the most advanced results with less computation .XCiT Is a common architecture , It can be easily deployed in other research fields , In these areas , Self attention has shown success .
边栏推荐
- MES系统,是企业生产的必要选择
- Easy to understand SSO
- Notes on PHP penetration test topics
- 【雅思口语】安娜口语学习记录 Part3
- It's too true. There's a reason why I haven't been rich
- ROS bridge notes (05) - Carla_ ackermann_ Control function package (convert Ackermann messages into carlaegovehiclecontrol messages)
- Standard function let and generic extension function in kotlin
- Wang Zijian: is the NFT of Tencent magic core worth buying?
- DeiT学习笔记
- Using helm to install rainbow in various kubernetes
猜你喜欢
调用 pytorch API完成线性回归

CTF-WEB shrine模板注入nmap的基本使用
Réplication de vulnérabilité - désrialisation fastjson

opencv学习笔记三——图像平滑/去噪处理

Leetcode medium question my schedule I

解析机器人科技发展观对社会研究论
![[step on the pit series] H5 cross domain problem of uniapp](/img/53/bd836a5c5545f51be929d8d123b961.png)
[step on the pit series] H5 cross domain problem of uniapp
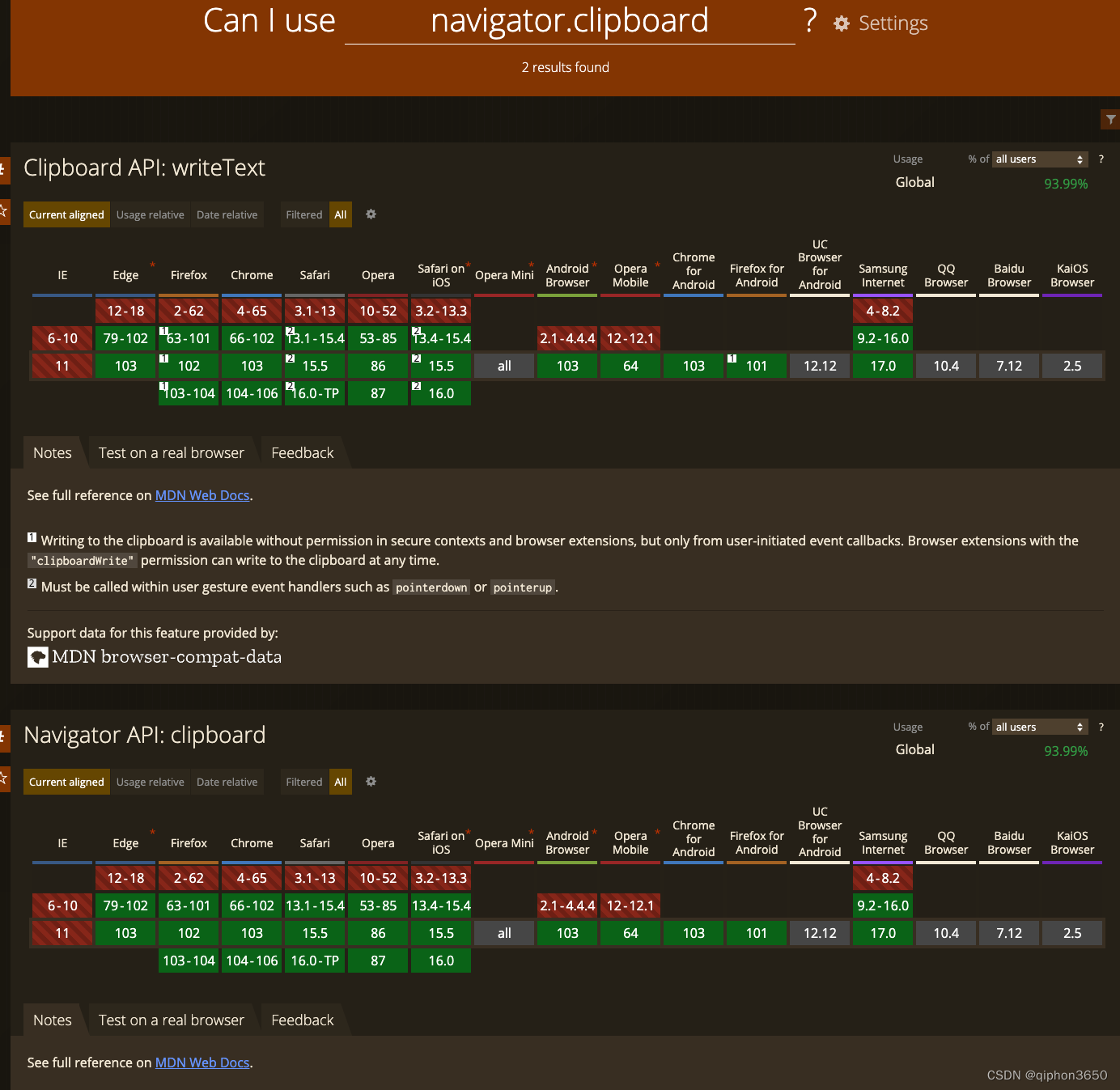
JS复制图片到剪切板 读取剪切板

Explore creativity in steam art design
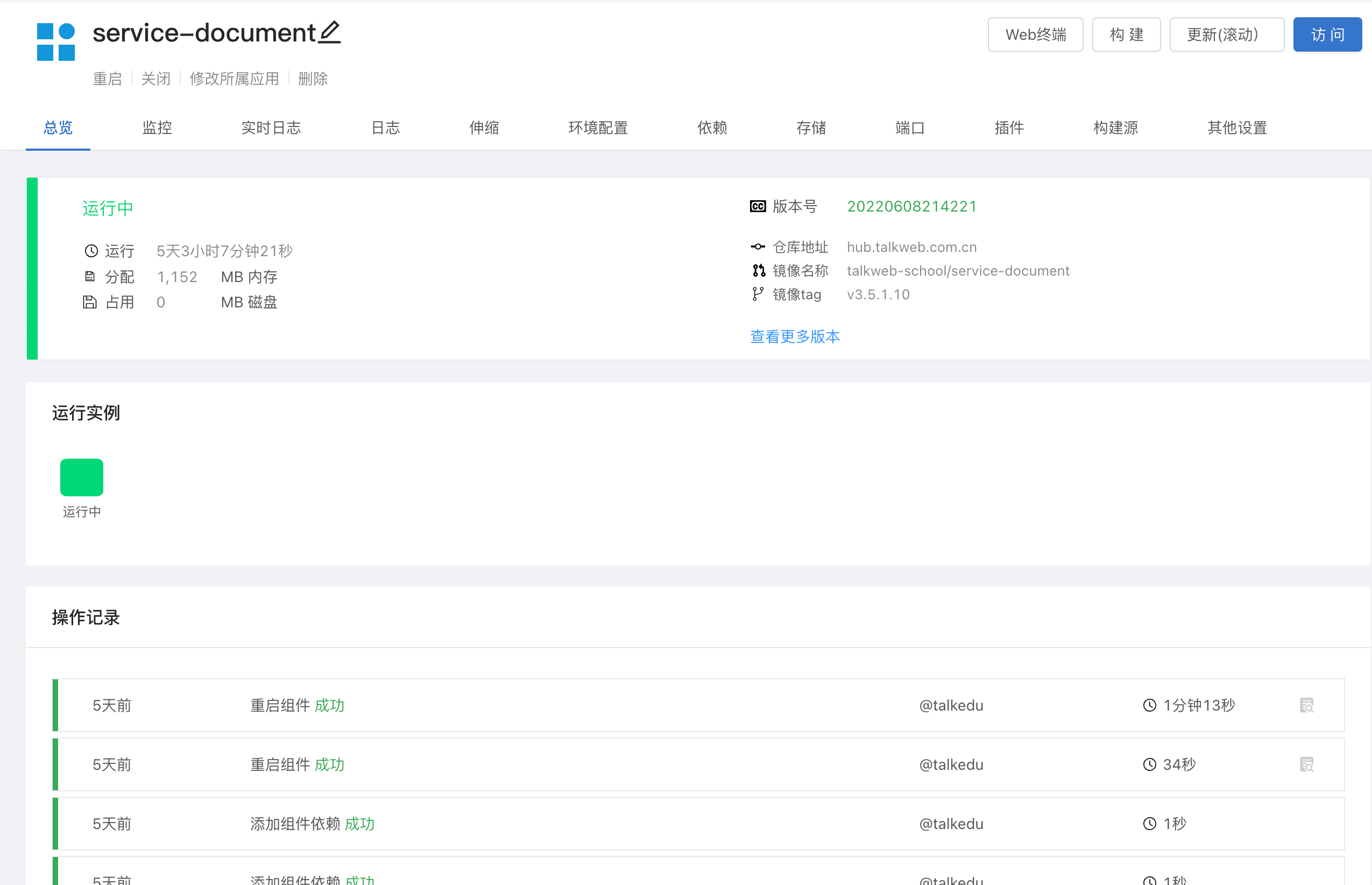
拓维信息使用 Rainbond 的云原生落地实践
随机推荐
ZCMU--1492: Problem D(C语言)
Wang Zijian: is the NFT of Tencent magic core worth buying?
Register of assembly language by Wang Shuang
Rainbond 5.6 版本发布,增加多种安装方式,优化拓扑图操作体验
One click installation of highly available Nacos clusters in rainbow
Use of any superclass and generic extension function in kotlin
JS复制图片到剪切板 读取剪切板
复杂网络建模(三)
Lua 编程学习笔记
Ebpf cilium practice (2) - underlying network observability
藏书馆App基于Rainbond实现云原生DevOps的实践
Splunk中single value视图使用将数值替换为文字
It took "7" years to build the robot framework into a micro service
CDC (change data capture technology), a powerful tool for real-time database synchronization
解析创新教育体系中的创客教育
Qinglong panel - today's headlines
复杂网络建模(一)
The reified keyword in kotlin is used for generics
Relevant data of current limiting
Analyzing the influence of robot science and technology development concept on Social Research