当前位置:网站首页>每日刷题记录 (十五)
每日刷题记录 (十五)
2022-07-06 15:41:00 【独一无二的哈密瓜】
文章目录
第一题: 剑指 Offer 57. 和为s的两个数字
LeetCode: 剑指 Offer 57. 和为s的两个数字
添加链接描述
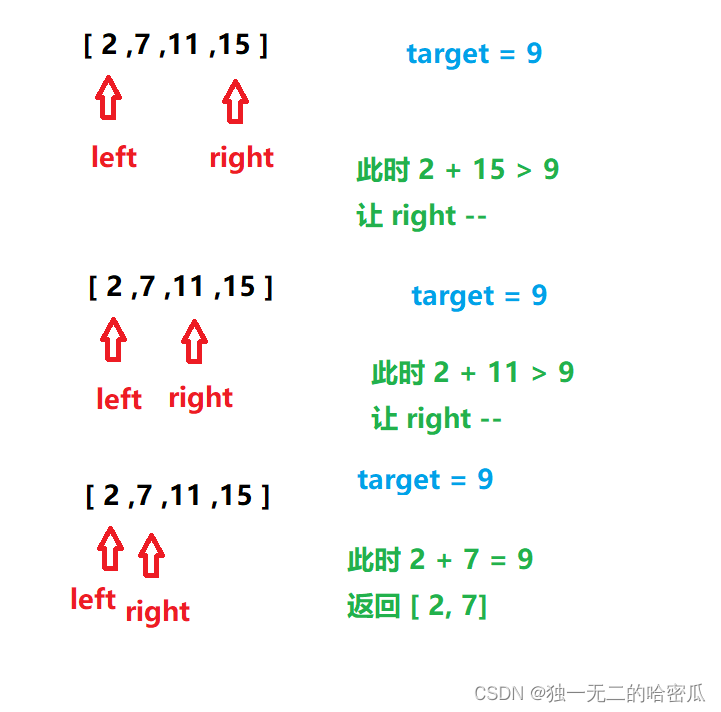
描述:
输入一个递增排序的数组和一个数字s,在数组中查找两个数,使得它们的和正好是s。如果有多对数字的和等于s,则输出任意一对即可。

解题思路:
- 这里题目中说数组
nums是递增排序. 可以使用双指针的方法- 用
left指向 0 下标, 用right指向nums.length-1下标- 如果
nums[left] + nums[right] > target, 此时和大了, 就选择小的数字, 让right--- 如果
nums[left] + nums[right] < target, 此时和小了, 就选择大的数组, 让left++- 如果此时
nums[left] + nums[right] = target, 返回该下标的值.
代码实现:
class Solution {
public int[] twoSum(int[] nums, int target) {
int left = 0;
int right = nums.length-1;
while(left < right) {
int total = nums[left] + nums[right];
if (total > target) {
right--;
}else if(total < target) {
left++;
}else{
return new int[]{
nums[left],nums[right]};
}
}
return new int[]{
};
}
}
第二题: 剑指 Offer 57 - II. 和为s的连续正数序列
LeetCode: 剑指 Offer 57 - II. 和为s的连续正数序列
描述:
输入一个正整数 target ,输出所有和为 target 的连续正整数序列(至少含有两个数)。
序列内的数字由小到大排列,不同序列按照首个数字从小到大排列。
解题思路:
- 这里也是使用双指针的办法.
- 让
left = 1, 让right=2, 从1, 2开始遍历- 数学中
1~n求和, 高斯定理,(n + 1) * (n - 1 + 1) / 2, 所以求得[left , right]的和为,(right+left) * (right-left+1) / 2- 如果当前求的和
total > target, 让left++- 如果当前求的和
total < target, 让right++- 如果当前求的和
total = target, 将 [left,right] 加入结果集中.并让left++(否则无法跳出循环)
代码实现:
class Solution {
public int[][] findContinuousSequence(int target) {
List<int[]> res = new ArrayList<>();
int left = 1;
int right = 2;
while(left < right) {
int total = (right + left) * (right - left + 1) / 2;
if(total > target) {
left++;
}else if(total < target){
right++;
}else{
int[] tmp = new int[right-left+1];
for(int i = 0; i < tmp.length; i++) {
tmp[i] = i + left;
}
res.add(tmp);
left++;
}
}
int[][] ans = new int[res.size()][];
for(int i = 0; i < res.size(); i++) {
ans[i] = res.get(i);
}
return ans;
}
}
第三题: 剑指 Offer 58 - I. 翻转单词顺序
LeetCode: 剑指 Offer 58 - I. 翻转单词顺序
描述:
输入一个英文句子,翻转句子中单词的顺序,但单词内字符的顺序不变。为简单起见,标点符号和普通字母一样处理。例如输入字符串"I am a student. “,则输出"student. a am I”。

解题思路:
- 对于本题, 首先对字符串进行去除首尾多余的空格.
- 然后根据空格,拆分成字符串数组
- 然后从后到前遍历, 记住, 可能出现多个空格的情况,
- 如果当前字符串为空, continue
5, 不为空, 直接添加当前的字符串, 然后注意添加空格的情况
代码实现:
class Solution {
public String reverseWords(String s) {
s = s.trim();
String[] str = s.split(" ");
StringBuilder sb = new StringBuilder();
for(int i = str.length-1; i >=0; i--) {
if(str[i].equals("")) continue;
sb.append(str[i]);
if(i != 0) {
sb.append(" ");
}
}
return sb.toString();
}
}
第四题: 剑指 Offer 59 - I. 滑动窗口的最大值
LeetCode: 剑指 Offer 59 - I. 滑动窗口的最大值
描述:
给定一个数组 nums 和滑动窗口的大小 k,请找出所有滑动窗口里的最大值。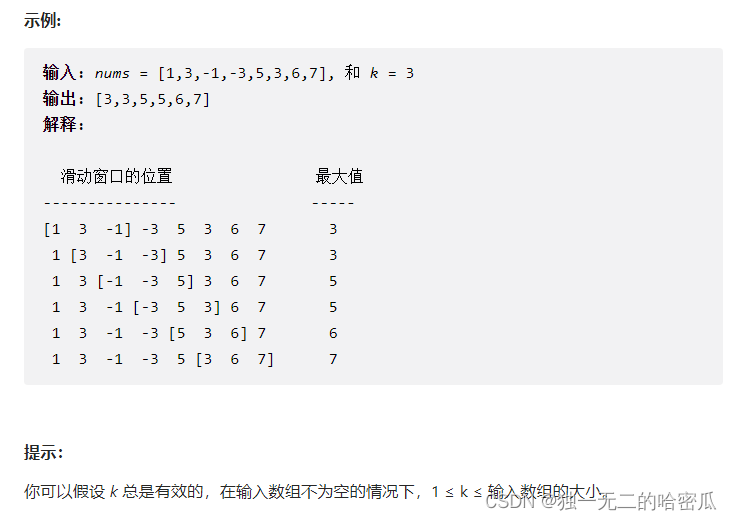
解题思路:
- 这里构造一个大小为 k 的滑动窗口
- 如果当前滑动窗口的左边界, 不在初始位置, 且 该窗口的右边界 > 前一个窗口的最大值, 那么直接让这个窗口的最大值等于前一个窗口的最大值.
- 如果当前滑动窗口的左边界不在初始位置, 且 该窗口的左边界的前一个值,小于前一个窗口的最大值, 那么, 就让该窗口的最大值等于前一个窗口的最小值.(因为新加入的值, 没有前一个窗口的最大值大, 要丢弃的值, 要比前一个窗口的最大值要小, 那么, 这个最大值就没有改变)
- 不满足2, 3 就直接遍历查找最大值.
- 最后返回每一个窗口的最大值.
代码实现:
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
if(nums.length == 0) return new int[]{
};
int left = 0;
int right = k - 1;
int[] ans = new int[nums.length-k+1];
while (right < nums.length) {
if(left > 0 && nums[right] > ans[left-1]) {
ans[left] = nums[right];
}else if(left > 0 && nums[left-1] < ans[left-1]){
ans[left] = ans[left-1];
}else {
int max = Integer.MIN_VALUE;
for(int i = left; i <= right; i++) {
max = Math.max(max,nums[i]);
}
ans[left] = max;
}
left++;
right++;
}
return ans;
}
}
第五题: 剑指 Offer 59 - II. 队列的最大值
LeetCode: 剑指 Offer 59 - II. 队列的最大值
描述:
请定义一个队列并实现函数 max_value 得到队列里的最大值,要求函数max_value、push_back 和 pop_front 的均摊时间复杂度都是O(1)。
若队列为空,pop_front 和 max_value 需要返回 -1

解题思路:
- 这题思路是使用一个队列, 添加元素. 使用一个双端队列, 进行对最大值的添加
- 在入队的时候, 判断当前双端队列是否为空, 不为空要进行比较
- 如果插入的value 要大于队尾元素, 就弹出队尾元素, 直到小于队尾元素, 或者队为空
- 这个双端队列中始终放的是目前队列的最大值.
- 出队的时候, 如果为空直接返回-1, 如果不为空. 比较队列和双端队列的队首值,是否一直, 如果不一致, 表示目前最大值还没有出队, 不用管. 此时只用出队首元素, 不需要出双端队列队首元素.
- 在得到最大值的时候, 如果队列为空就返回-1, 如果不为空, 直接返回双端队列的队首元素.
代码实现:
class MaxQueue {
private Queue<Integer> res;
private Deque<Integer> tmp;
public MaxQueue() {
res = new LinkedList<>();
tmp = new LinkedList<>();
}
public int max_value() {
if(res.isEmpty()) {
return -1;
}
return tmp.peekFirst();
}
public void push_back(int value) {
res.offer(value);
while(!tmp.isEmpty() && value > tmp.peekLast()) {
tmp.pollLast();
}
tmp.offerLast(value);
}
public int pop_front() {
if(res.isEmpty()) {
return -1;
}
int val = res.poll();
if(val == tmp.peekFirst()){
tmp.pollFirst();
}
return val;
}
}
/** * Your MaxQueue object will be instantiated and called as such: * MaxQueue obj = new MaxQueue(); * int param_1 = obj.max_value(); * obj.push_back(value); * int param_3 = obj.pop_front(); */
第六题: 剑指 Offer 60. n个骰子的点数
LeetCode: 剑指 Offer 60. n个骰子的点数
描述:
把n个骰子扔在地上,所有骰子朝上一面的点数之和为s。输入n,打印出s的所有可能的值出现的概率。
你需要用一个浮点数数组返回答案,其中第 i 个元素代表这 n 个骰子所能掷出的点数集合中第 i 小的那个的概率。

解题思路:
- 这里使用动态规划
- 动态规划思路:
- 状态 F(i,j): 表示投了i个筛子, 点数为 j 的概率
- 状态转移方程: F(i,j) = dp[i-1][j-k] * 1/6 (j>k)
- 初始状态: F(1,j) = 1/6;
- 返回结果: F
代码实现:
class Solution {
public double[] dicesProbability(int n) {
// 点数j [1~6*n]
double[][] dp = new double[n+1][6*n+1];
// 初始状态
for (int i = 1; i <= 6; i++) {
dp[1][i] = 1/6.0;
}
for(int i = 2; i <= n; i++) {
// j的范围[i,6i]
for(int j = i; j <= 6*i; j++) {
for(int k = 1; k <= 6; k++) {
// 当 j > k 的时候,求的点数才有可能否者不可能丢出0 -1
if(j>k) {
dp[i][j] += dp[i-1][j-k] * 1 / 6.0;
}else{
// 只要这里 j<=k, 后面的情况只会更小, 直接跳过
break;
}
}
}
}
// n个筛子,结果是[n,6n], 一共有, (6n-n)+1 = 5n+1个数
double[] res = new double[5*n+1];
for(int i = 0; i < 5 * n + 1; i++) {
res[i] = dp[n][n+i];
}
return res;
}
}
第七题: 剑指 Offer 61. 扑克牌中的顺子
LeetCode: 剑指 Offer 61. 扑克牌中的顺子
描述:
从若干副扑克牌中随机抽 5 张牌,判断是不是一个顺子,即这5张牌是不是连续的。2~10为数字本身,A为1,J为11,Q为12,K为13,而大、小王为 0 ,可以看成任意数字。A 不能视为 14。

解题思路:
- 本题的意思就是, 0可以当成别的牌
- 这里首先进行排序.
- 然后记录 zero 的次数
- zero记录完之后, 查看两个数组是否相差为1,
- 如果相差为1, 继续
- 如果两个相等, 直接返回false;
- 如果相差还有别的情况, 得到相差的牌数, 计算公式
right - left -1, 根据这个数据, 查看zero是否足够, 如果zero<0 直接返回false.- 遍历结束, 返回true
代码实现:
class Solution {
public boolean isStraight(int[] nums) {
Arrays.sort(nums);
int zero = 0;
int index = 0;
for(int i = 0; i < nums.length - 1; i++) {
if (nums[i] == 0) {
zero++;
}else{
if(nums[i] == nums[i+1]) {
return false;
}
if(nums[i+1] - nums[i] != 1){
zero -= nums[i+1] - nums[i] - 1;
if(zero < 0) return false;
}
}
}
return true;
}
}
边栏推荐
- Detailed explanation of ThreadLocal
- ICLR 2022 | 基于对抗自注意力机制的预训练语言模型
- Dayu200 experience officer runs the intelligent drying system page based on arkui ETS on dayu200
- 机器人材料整理中的套-假-大-空话
- ACL 2022 | small sample ner of sequence annotation: dual tower Bert model integrating tag semantics
- Gpt-3 is a peer review online when it has been submitted for its own research
- MySQL authentication bypass vulnerability (cve-2012-2122)
- DevSecOps软件研发安全实践——发布篇
- 企业不想换掉用了十年的老系统
- Machine test question 1
猜你喜欢
Dayu200 experience officer homepage AITO video & Canvas drawing dashboard (ETS)
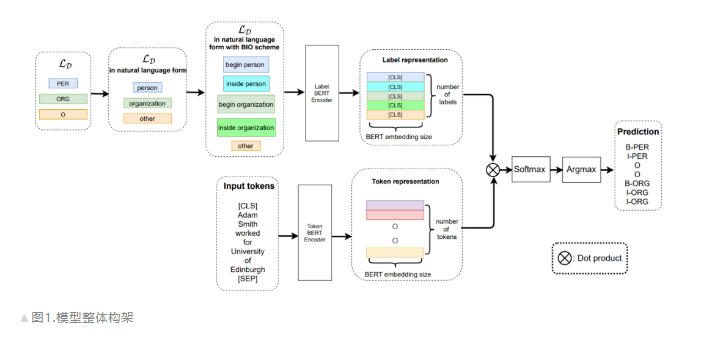
ACL 2022 | small sample ner of sequence annotation: dual tower Bert model integrating tag semantics

室内LED显示屏应该怎么选择?这5点注意事项必须考虑在内

#DAYU200体验官# 首页aito视频&Canvas绘制仪表盘(ets)
Thinkphp5 multi table associative query method join queries two database tables, and the query results are spliced and returned
docker启动mysql及-eMYSQL_ROOT_PASSWORD=my-secret-pw问题解决
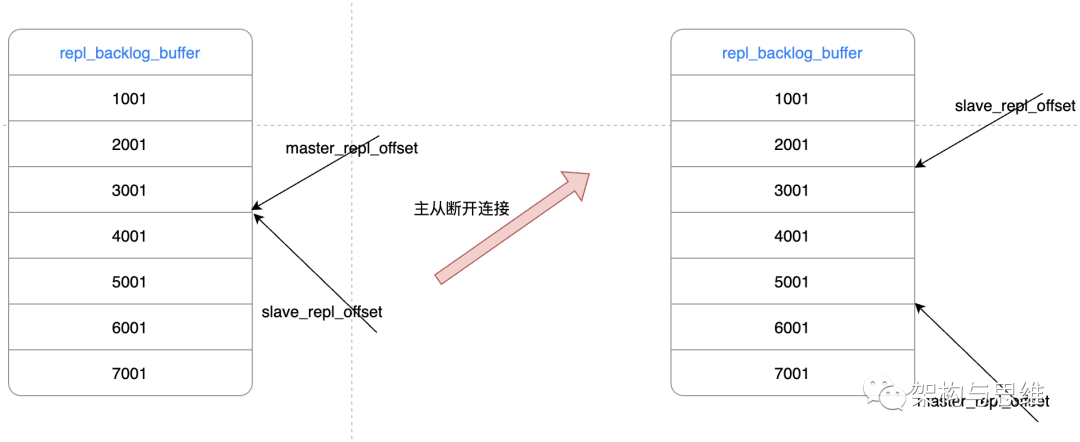
【全网首发】Redis系列3:高可用之主从架构的
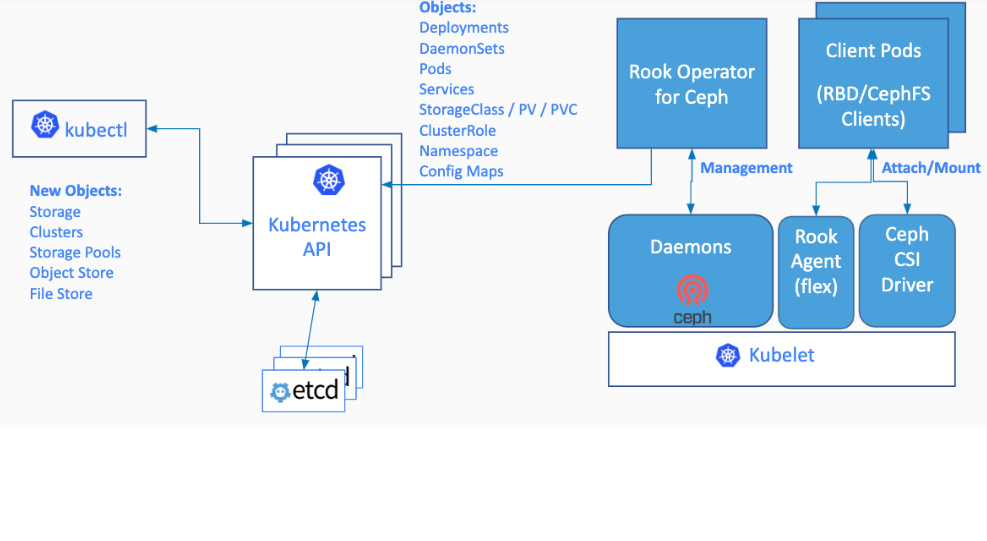
Cloud native (32) | kubernetes introduction to platform storage system
None of the strongest kings in the monitoring industry!

Coscon'22 community convening order is coming! Open the world, invite all communities to embrace open source and open a new world~
随机推荐
ICLR 2022 | 基于对抗自注意力机制的预训练语言模型
Unified Focal loss: Generalising Dice and cross entropy-based losses to handle class imbalanced medi
Jafka source analysis processor
B站大佬用我的世界搞出卷積神經網絡,LeCun轉發!爆肝6個月,播放破百萬
动作捕捉用于蛇运动分析及蛇形机器人开发
Devsecops software R & D security practice - release
MATLAB小技巧(27)灰色预测
安全保护能力是什么意思?等保不同级别保护能力分别是怎样?
spark调优(二):UDF减少JOIN和判断
The problem that dockermysql cannot be accessed by the host machine is solved
[unity] upgraded version · Excel data analysis, automatically create corresponding C classes, automatically create scriptableobject generation classes, and automatically serialize asset files
Matlab tips (27) grey prediction
Case recommendation: An Qing works with partners to ensure that the "smart court" is more efficient
A few suggestions for making rust library more beautiful! Have you learned?
Machine test question 1
Motion capture for snake motion analysis and snake robot development
Hard core observation 545 50 years ago, Apollo 15 made a feather landing experiment on the moon
Demonstration of the development case of DAPP system for money deposit and interest bearing financial management
石墨文档:4大对策解决企业文件信息安全问题
koa2对Json数组增删改查