Storage of data

One 、 Data type introduction

char           // Character data type  1
short          // Short  2
int            // plastic  4
long           // Long integer  4(32 position )/8（64 position ）
long long      // Longer plastic surgery  8 C99
float          // Single-precision floating-point  4
double         // Double precision floating point  8

The meaning of type :

1. Use this type to exploit the size of memory space （ Size determines the range of use ）.
2. Look at memory space from different perspectives .

1.1 Basic classification of types

（1） Plastic surgery Family

（2） Floating point family

（3） Construction type

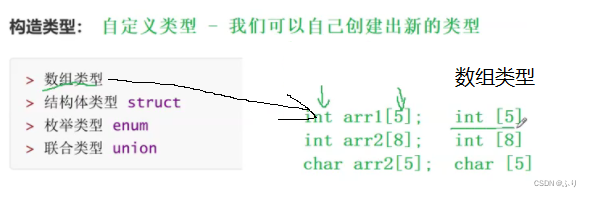
notes ： The rest will be explained later

（4） Pointer types

（5） Empty type

1. void Indicates empty type （ No type ）
2. Usually applied to the return type of a function 、 The parameters of the function 、 Pointer types

#include <stdio.h>
// first  void  Indicates that the function will not return a value  ( Function return type )
// the second  void  Indicates that the function does not require any arguments  （ Function parameter type ）
void test(void)
{
    
	printf("hehe\n");
}
int main()
{
    
	printf("hehehe\n");
	test();
	return 0;
}

Two 、 Shaping storage in memory

The creation of a variable is to open up space in memory . The size of space is determined according to different types .

#include <stdio.h>

// Values have different representations 
//2 Base number 
//8 Base number 
//10 Base number 
//16 Base number 
// Decimal 21
//0b10101
//025
//21
//0x1

int main()
{
    
	int a = 20;
	int b = -10;
	  
	return 0;
}

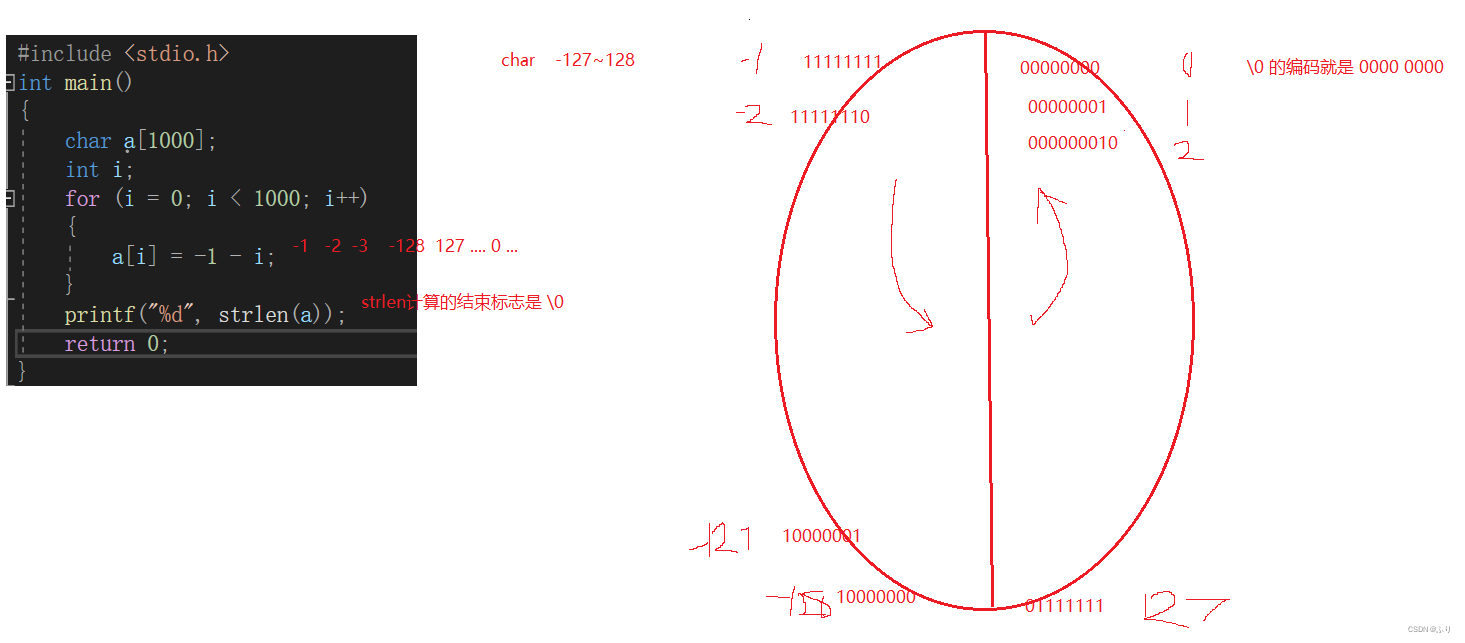
2.1 Original code 、 Inverse code 、 Complement code

#include <stdio.h>

// Values have different representations 
//2 Base number 
//8 Base number 
//10 Base number 
//16 Base number 
// Decimal 21
//0b10101
//025
//21
//0x1

//
// The integer 2 There are three representations of base 
//1.  Positive integer ,  Original code 、 Inverse code 、 The complement is the same 
//2.  Negative integer ,  Original code 、 Inverse code 、 Complement needs to be calculated 
// Original code  ：  The binary sequence written directly in positive and negative form is the original code 
// Inverse code  ：  The sign bit of the original code remains the same , Other bits are reversed 
// Complement code  ：  Inverse code  + 1  It's complement 
//


int main()
{
    
	int a = 20;
	//20
	//0000 0000 0000 0000 0000 0000 0001 0100
	//0x00 00 00 14  Hexadecimal 
	int b = -10;
	//-10
	//1000 0000 0000 0000 0000 0000 0000 1010 --  Original code 
	// 0x80 00 00 00 0a
	//1111 1111 1111 1111 1111 1111 1111 0101 --  Inverse code 
	// 0xfffffff5
	//1111 1111 1111 1111 1111 1111 1111 1010 --  Complement code 
	//0xfffffff6 
	return 0;
}

&a

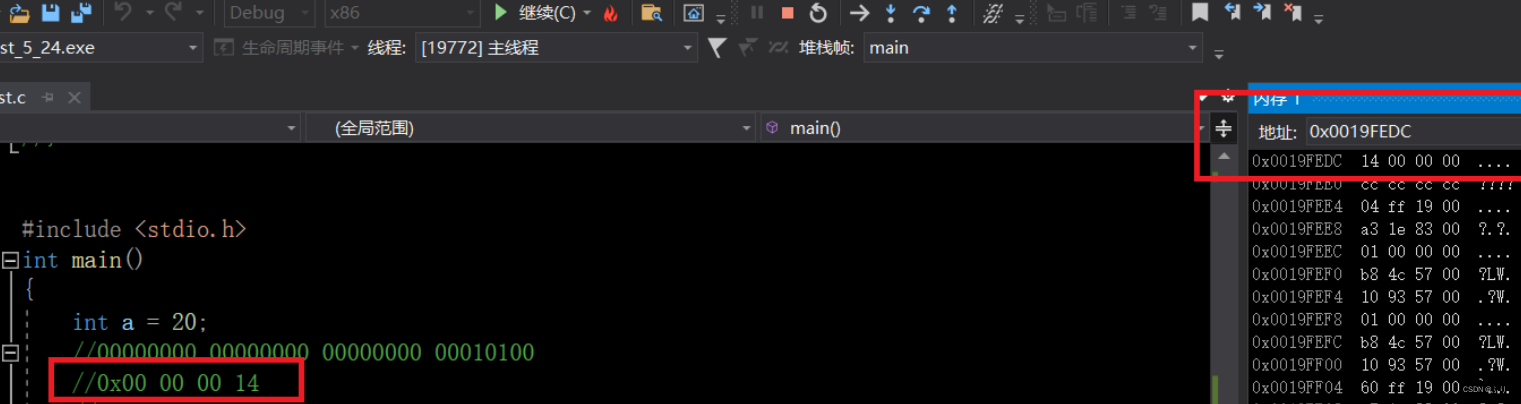
We can see that for a and b The complement code is stored separately . But we found something wrong with the order .
That's why ？

2.2 Introduction to big and small end

What big end, small end ：

1. Big end （ Storage ） Pattern , The low bit of data is stored in the high address of memory , And the high end of the data , Stored in a low address in memory ;
2. The small end （ Storage ） Pattern , The low bit of data is stored in the low address of memory , And the high end of the data ,, Stored in memory
   Address .

Why are there big and small ends

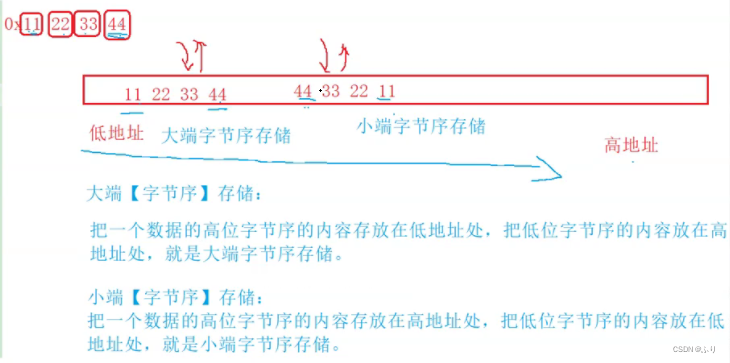
notes ：0x 11 22 33 44 The high position is 11 , The low position is 44 , Be similar to 150 , The high position is 1
The low position is 0

Baidu 2015 System Engineer written test questions ：

// Please briefly describe the concepts of big end byte order and small end byte order ,
// Design a small program to determine the current machine byte order .（10 branch ）

#include <stdio.h>
int check()
{
    
	int i = 1;
	//&i  Get the first address  , Force type to  char*  Type and then dereference to get  00  still  01
	return (*(char*)&i);
}
int main()
{
    
	int ret = check();
	if (ret == 1)
	{
    
		printf(" The small end \n");
	}
	else
	{
    
		printf(" Big end \n");
	}
	return 0;
}

2.4 practice

One 、

// What output ？
#include <stdio.h>
int main()
{
    
    char a= -1;
    signed char b=-1;
    unsigned char c=-1;
    printf("a=%d,b=%d,c=%d",a,b,c);
    return 0; 
}

Two 、

2.
#include <stdio.h>
int main()
{
    
    char a = -128;
    printf("%u\n",a);
    return 0; 
}

3、 ... and 、

#include <stdio.h>
int main()
{
    
    char a = 128;
    printf("%u\n",a);
    printf("%d\n", a);
    return 0;
 }

Four 、

#include <stdio.h>
int main()
{
    
	int i = -20;
	unsigned int j = 10;
	return 0;
}

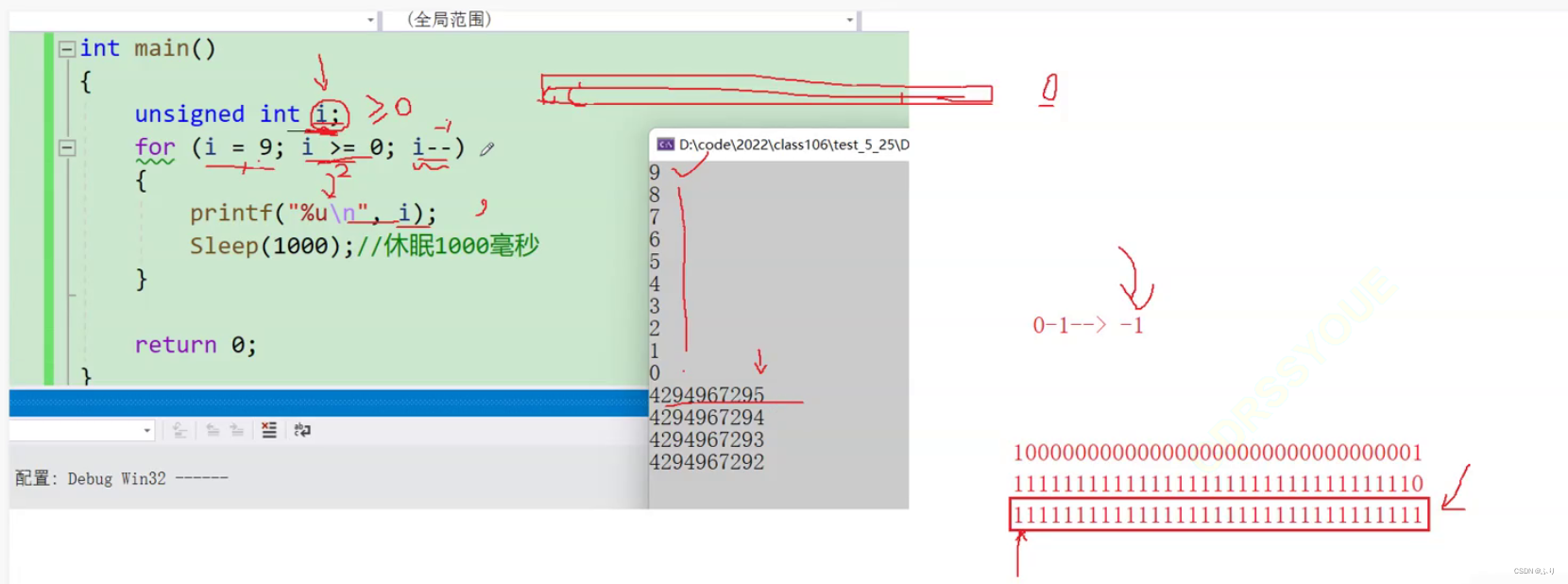
5、 ... and 、

#include <stdio.h>
#include <windows.h>
int main()
{
    
	unsigned int i;
	for (i = 9; i >= 0; i--) 
	{
    
		printf("%u\n", i);
		Sleep(1000);
	}
	return 0;
}

6、 ... and 、

#include <stdio.h>
int main()
{
    
	char a[1000];
	int i;
	for (i = 0; i < 1000; i++)
	{
    
		a[i] = -1 - i;
	}
	printf("%d", strlen(a));
	return 0;
}

7、 ... and 、

#include <stdio.h>
unsigned char i = 0;
int main()
{
    
	for (i = 0;i <= 255;i++)
	{
    
		printf("hello world\n");
	}
	return 0;
}

answer

// char  Signed number  -128 ~ 127
//  An unsigned number  0 ~ 255
#include <stdio.h>
int main()
{
    
    char a = -1;
    //1000 0000 0000 0000 0000 0000 0001
    //1111 1111 1111 1111 1111 1111 1110
    //1111 1111 1111 1111 1111 1111 1111
    // truncation 
    //11111111 - a %d It's a signed integer 
    // Improve the overall shape 
    //1111 1111 1111 1111 1111 1111 1111 1111 -  Complement in memory 
    //1000 0000 0000 0000 0000 0000 0000 0000
    //1000 0000 0000 0000 0000 0000 0000 0001 -> -1

    signed char b = -1;
    unsigned char c = -1;
    // Unsigned integer raised high order direct complement  0
    printf("a=%d,b=%d,c=%d", a, b, c);
    return 0;
}

#include <stdio.h>
int main()
{
    
	char a = -128;
	//1000 0000 0000 0000 0000 0000 0100 0000
	//1111 1111 1111 1111 1111 1111 0111 1111
	//1111 1111 1111 1111 1111 1111 1000 0000 - truncation 
	//10000000 - a
	//1111 1111 1111 1111 1111 1111 1000 0000 -  promote 
	//
	printf("%u\n", a);
	return 0;
}

#include <stdio.h>
int main()
{
    
	char a = 128;
	//0000 0000 0000 0000 0000 0000 1000 0000
	//0111 1111 1111 1111 1111 1111 0111 1111
	//0111 1111 1111 1111 1111 1111 1000 0000 -  truncation 
	//1000 0000 - a
	//1111 1111 1111 1111 1111 1111 1000 0000 -  promote 
	printf("%u\n", a);
	//1000 0000 - a
	//1111 1111 1111 1111 1111 1111 1000 0000 -  promote 
	//1000 0000 0000 0000 0000 0000 0111 1111
	//1000 0000 0000 0000 0000 0000 1000 0000
	printf("%d\n", a);
	return 0;
}

#include <stdio.h>
int main()
{
    
	int i = -20;
	// -20
	//1000 0000 0000 0000 0000 0000 0001 0100
	//1111 1111 1111 1111 1111 1111 1110 1011
	//1111 1111 1111 1111 1111 1111 1110 1100 -> -20 Complement  

	unsigned int j = 10;
	//0000 0000 0000 0000 0000 0000 0000 1010
	printf("%d\n", i + j);
	//1111 1111 1111 1111 1111 1111 1110 1100
	//0000 0000 0000 0000 0000 0000 0001 1010
	//1111 1111 1111 1111 1111 1111 1111 0110
	// 
	//1000 0000 0000 0000 0000 0000 0000 1001
	//1000 0000 0000 0000 0000 0000 0000 1010
	return 0;
}

6.
7 .

#include <stdio.h>
unsigned char i = 0;
//unsigned char  Type value range  0~255  So Heng holds 
int main()
{
    
	for (i = 0;i <= 255;i++)
	{
    
		printf("hello world\n");
	}
	return 0;
}


// Dead cycle 

important

#include <stdio.h>
#include <string.h>
int main()
{
    
	if (strlen("abc") - strlen("abcdef") > 0)
	{
    
		//strlen  The type returned by the function is an unsigned integer , For two unsigned reshapes, see the result or unsigned reshape 
		printf(">\n");
		printf("%u\n", strlen("abc") - strlen("abcdef"));   //4294967293
	}
	else
	{
    
		printf("<\n");
	}
	return 0;
}


// If you want to calculate, you can force type conversion from integer or comparison size 

3、 ... and 、 Floating point storage in memory

 Common floating point numbers ：
3.14159
1E10             1.0*pow(10,10)
 The family of floating-point numbers includes ：  float、double、long double  type .
 The range represented by floating point numbers ： float.h In the definition of 

They are included in these header files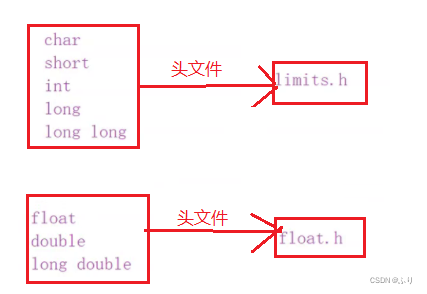

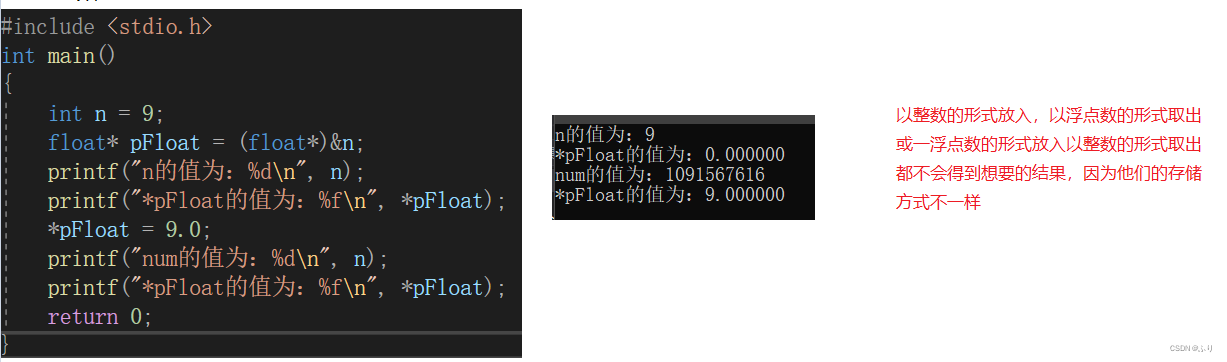
3.1 An example

#include <stdio.h>
int main()
{
    
	int n = 9;
	float* pFloat = (float*)&n;
	printf("n The value of is ：%d\n", n);
	printf("*pFloat The value of is ：%f\n", *pFloat);
	*pFloat = 9.0;
	printf("num The value of is ：%d\n", n);
	printf("*pFloat The value of is ：%f\n", *pFloat);
	return 0;
}

3.2 Floating point storage rules

num and *pFloat It's the same number in memory , Why are the interpretation results of floating-point numbers and integers so different ？

To understand this result , Be sure to understand the representation of floating-point numbers in the computer .

Detailed interpretation ：

According to international standards IEEE（ Institute of electrical and Electronic Engineering ） 754, Any binary floating point number V It can be expressed in the following form ：

1. (-1)^S * M * 2^E
2. (-1)^s The sign bit , When s=0,V Is a positive number ; When s=1,V It's a negative number .
3. M Represents a significant number , Greater than or equal to 1, Less than 2.
4. 2^E Indicates the index bit .

for instance ：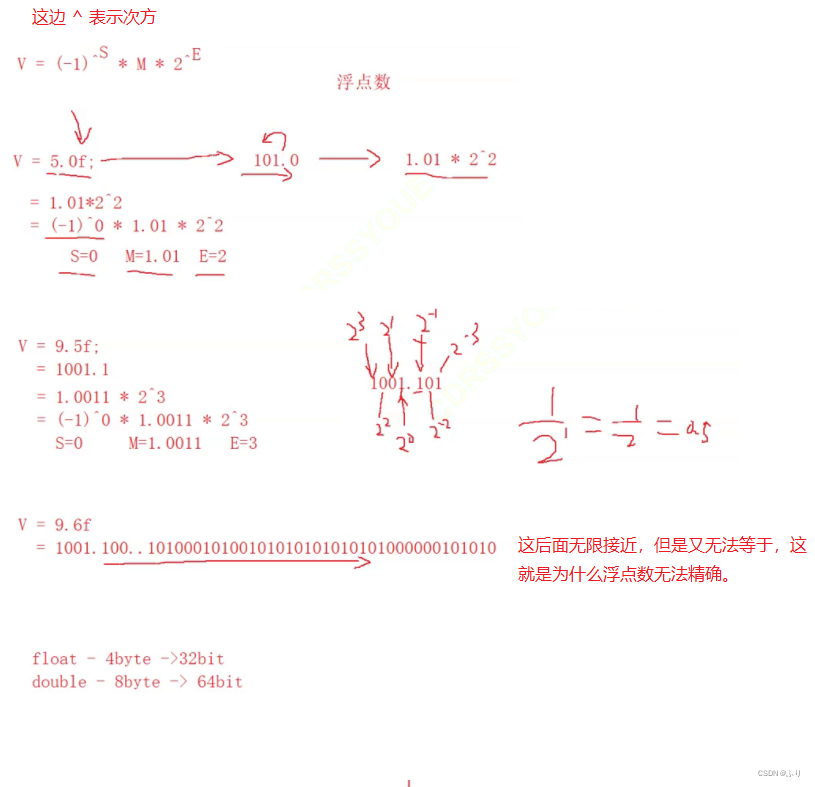

First ,E For an unsigned integer （unsigned int）

1. It means , If E by 8 position , Its value range is 0 ~ 255;
2. If E by 11 position , Its value range is 0~2047.
3. however , We know , In scientific counting E You can have negative numbers , therefore IEEE754 Regulations ：

Deposit in Memory time E The true value of must be added with an intermediate number ,
about 8 Bit E, The middle number is 127;
about 11 Bit E, The middle number is 1023.

such as ,2^10 Of E yes 10, So save it as 32 When floating-point numbers are in place , Must be saved as 10+127=137, namely 10001001.

Index E Fetching from memory can be further divided into three cases ：

At this time , Floating point numbers are represented by the following rules , The index E The calculated value of minus 127（ or 1023）, Get the real value , then
Significant figures M Add the first 1.
such as ：
0.5（1/2） The binary form of is 0.1, Since it is stipulated that the positive part must be 1, That is to move the decimal point to the right 1 position , Then for 1.0*2^(-1), Its order code is -1+127=126, Expressed as 01111110, And the mantissa 1.0 Remove the integer part and make it 0, A filling 0 To 2300000000000000000000000, Then its binary representation is :

0 01111110 00000000000000000000000

E All for 0

At this time , The exponent of a floating point number E be equal to 1-127（ perhaps 1-1023） That's the true value ,
Significant figures M No more first 1, It's reduced to 0.xxxxxx Decimals of . This is to show that ±0, And close to
0 A very small number of .

E All for 1

At this time , If the significant number M All for 0, Express ± infinity （ It depends on the sign bit s）;

Explain the previous topic ：

Why? 0x00000009 Restore to floating point number , became 0.000000 ？

First , take 0x00000009 Split , Get the first sign bit s=0, Back 8 Bit index E=00000000 , Last 23 A significant number of bits M=000 0000 0000 0000 0000 1001.

9 -> 0000 0000 0000 0000 0000 0000 0000 1001

Because the index E All for 0, So the second case in the previous section . therefore , Floating point numbers V The just ：

obviously ,V It's a very small one, close to 0 Positive number of , So the decimal number is 0.000000.

Let's look at the second part of the example .

Floating point number 9.0, How to express... In binary ？ How much is it to restore to decimal ？

9.0 -> 1001.0 ->(-1)^01.00123 -> s=0, M=1.001,E=3+127=130

First , Floating point numbers 9.0 Equal to binary 1001.0, namely 1.001×2^3.

that , The first sign bit s=0, Significant figures M be equal to 001 Add... To the back 20 individual 0, Cramming 23 position , Index E etc. 3+127=130, namely 10000010.

therefore , Written in binary form , Should be s+E+M, namely

0 10000010 001 0000 0000 0000 0000 0000

This 32 The binary number of bits , Restore to decimal , It is 1091567616 .