当前位置:网站首页>Leetcode (215) -- the kth largest element in the array
Leetcode (215) -- the kth largest element in the array
2022-07-04 07:35:00 【SmileGuy17】
Leetcode(215)—— The... In the array K The biggest element
subject
Given an array of integers nums And integer k, Please return the... In the array k The biggest element .
Please note that , What you need to look for is the number after array sorting k The biggest element , Not the first. k A different element .
Example 1:
Input : [3,2,1,5,6,4] and k = 2
Output : 5
Example 2: Input : [3,2,3,1,2,4,5,5,6] and k = 4
Output : 4
Tips :
- 1 1 1 <= k <= nums.length <= 1 0 4 10^4 104
- − 1 0 4 -10^4 −104 <= nums[i] <= 1 0 4 10^4 104
Answer key
Method 1 : Bubble sort
Ideas
The principle of bubble sorting
Code implementation
my :
class Solution {
public:
int findKthLargest(vector<int>& nums, int k) {
int n = nums.size();
if(n == 1) return nums[0];
bool swapped;
for(int i = 0; i < n; i++){
swapped = false;
for(int t = 0; t < n-i-1; t++){
if(nums[t] < nums[t+1]){
swap(nums[t], nums[t+1]);
swapped = true;
}
}
if(!swapped) break;
}
return nums[k-1];
}
};
Complexity analysis
Time complexity : O ( n log n ) O(n \log n) O(nlogn)
Spatial complexity : O ( 1 ) O(1) O(1)
Method 2 : Simple selection sort
Ideas
The principle of simple selection sorting
Code implementation
my :
class Solution {
public:
int findKthLargest(vector<int>& nums, int k) {
int n = nums.size();
if(n == 1) return nums[0];
int max, tmp;
for(int i = 0; i < n; i++){
max = i;
for(int t = i+1; t < n; t++){
if(nums[max] < nums[t]) max = t;
}
tmp = nums[i];
nums[i] = nums[max];
nums[max] = tmp;
}
return nums[k-1];
}
};
Complexity analysis
Time complexity : O ( n log n ) O(n \log n) O(nlogn)
Spatial complexity : O ( 1 ) O(1) O(1)
Method 3 : Direct insert sort
Ideas
The principle of direct insertion sort
Code implementation
my :
class Solution {
public:
int findKthLargest(vector<int>& nums, int k) {
int n = nums.size();
if(n == 1) return nums[0];
for(int i = 1; i < n; i++){
// Set the length of the first element as 1 Sequence , So start sorting from the second element
for(int t = i; t > 0 && nums[t] > nums[t-1]; t--)
swap(nums[t], nums[t-1]);
}
return nums[k-1];
}
};
Complexity analysis
Time complexity : O ( n log n ) O(n \log n) O(nlogn)
Spatial complexity : O ( 1 ) O(1) O(1)
Method four : Shell Sort
Ideas
The principle of hill ordering
Code implementation
my :
class Solution {
public:
int findKthLargest(vector<int>& nums, int k) {
int n = nums.size();
if(n == 1) return nums[0];
int increment = n/3+1; // The minimum guarantee is 1
while(increment > 0){
// Direct insert sort
for(int i = 0; i < n; i++){
for(int t = i; t-increment >= 0 && nums[t] > nums[t-increment]; t -= increment)
swap(nums[t], nums[t-increment]);
}
increment--;
}
return nums[k-1];
}
};
Complexity analysis
Time complexity : O ( n 3 / 2 ) O(n^{3/2}) O(n3/2)
Spatial complexity : O ( 1 ) O(1) O(1)
Method five : Merge sort
Ideas
The principle of merging and sorting
Code implementation
my ( recursive ):
class Solution {
void MSort(vector<int>& nums, int l, int r){
if(l == r)
nums[l] = nums[l];
else{
vector<int> Tmp(r-l+1);
int mid = (l+r)/2;
MSort(nums, l, mid);
MSort(nums, mid+1, r);
// Merge the above two groups
int p1 = l, p2 = mid+1, p = 0;
while(p1 <= mid && p2 <= r){
if(nums[p1] < nums[p2])
Tmp[p++] = nums[p2++];
else Tmp[p++] = nums[p1++];
}
if(p1 <= mid)
while(p1 <= mid) Tmp[p++] = nums[p1++];
if(p2 <= r)
while(p2 <= r) Tmp[p++] = nums[p2++];
p = 0;
while(l <= r)
nums[l++] = Tmp[p++];
}
}
public:
int findKthLargest(vector<int>& nums, int k) {
if(nums.size() == 1) return nums[0];
// for(int i = 0; i < n; i++){}
// Merge sort
MSort(nums, 0, nums.size()-1);
return nums[k-1];
}
};
Complexity analysis
Time complexity : O ( n log n ) O(n \log n) O(nlogn)
Spatial complexity : O ( n ) O(n) O(n)
Methods six : Quick sort ( improvement ——「 Choose... Quickly 」 Algorithm )
Ideas
There must be operations to disrupt the array , That is, the pivot selection is not fixed , Otherwise, it is easy to encounter extreme situations, resulting in a time complexity of O ( n 2 ) O(n^2) O(n2).
We can use quick sorting to solve this problem , First sort the original array , And back to the penultimate k k k A place , The average time complexity is O ( n log n ) O(n \log n) O(nlogn), But in fact, we can do it faster .
First, let's review the quick sort , This is a typical divide and conquer algorithm . Let's look at arrays a [ l ⋯ r ] a[l \cdots r] a[l⋯r] The process of quick sorting is ( Reference resources 《 Introduction to algorithms 》):
- decompose : Will array a [ l ⋯ r ] a[l \cdots r] a[l⋯r] 「 Divide 」 Into two subarrays a [ l ⋯ q − 1 ] a[l \cdots q - 1] a[l⋯q−1]]、 a [ q + 1 ⋯ r ] a[q + 1 \cdots r] a[q+1⋯r], bring a [ l ⋯ q − 1 ] a[l \cdots q - 1] a[l⋯q−1] Each element in is less than or equal to a [ q ] a[q] a[q], And a [ q ] a[q] a[q] Less than or equal to a [ q + 1 ⋯ r ] a[q + 1 \cdots r] a[q+1⋯r] Every element in . among , Calculate subscript q q q It's also 「 Divide 」 Part of the process .
- solve : Fast sort through recursive calls , Pair arrays a [ l ⋯ q − 1 ] a[l \cdots q - 1] a[l⋯q−1] and a [ q + 1 ⋯ r ] a[q + 1 \cdots r] a[q+1⋯r] Sort .
- Merge : Because subarrays are sorted in place , So there is no need to merge , a [ l ⋯ r ] a[l \cdots r] a[l⋯r] It's in order .
- As mentioned above 「 Divide 」 The process is : From subarray a [ l ⋯ r ] a[l \cdots r] a[l⋯r] Select any element in x x x As principal element , Adjust the elements of the subarray so that the elements on the left are less than or equal to it , The elements on the right are greater than or equal to it , x x x The final position of the is q q q.
From this we can find that every time we pass 「 Divide 」 After the operation , We must be able to determine the final position of an element , namely x x x The final position of the is q q q, And guarantee a [ l ⋯ q − 1 ] a[l \cdots q - 1] a[l⋯q−1] Each element in is less than or equal to a [ q ] a[q] a[q], And a [ q ] a[q] a[q] Less than or equal to a [ q + 1 ⋯ r ] a[q + 1 \cdots r] a[q+1⋯r] Every element in . therefore As long as a certain division q q q It's the penultimate k k k When subscript , We have found the answer . We only care about this , as for a [ l ⋯ q − 1 ] a[l \cdots q - 1] a[l⋯q−1] and a [ q + 1 ⋯ r ] a[q+1 \cdots r] a[q+1⋯r] Whether it's orderly , We don't care .
therefore , We can Improve the quick sort algorithm To solve this problem :
In the process of decomposition , We'll divide the subarray , If you divide it up q q q Just the subscript we need ( That is, when you encounter k == q-1, here a [ q ] a[q] a[q] Sinister k − 1 k-1 k−1 Each element is greater than or equal to it , The elements on the right are less than or equal to it ), Go straight back a [ q ] a[q] a[q]; otherwise , If q q q Smaller than the target subscript , Just recurse the right subinterval , Otherwise, recursive left subinterval .
In this way, we can change the original recursive two intervals into only recursive one interval , Improved time efficiency . This is it. 「 Choose... Quickly 」 Algorithm .
We know the performance of quicksort and 「 Divide 」 The length of the subarray is closely related to . Intuitively understand if each time the scale is n n n We are all divided into 1 1 1 and n − 1 n - 1 n−1, Every time I recurse, I send it to n − 1 n - 1 n−1 Recursion in the collection of , This situation is the worst , The price of time is O ( n 2 ) O(n ^ 2) O(n2). We can introduce randomization to accelerate this process , The expectation of its time cost is O ( n ) O(n) O(n), The proof process can refer to 「《 Introduction to algorithms 》9.2: The selection algorithm expected to be linear 」.
Code implementation
Leetcode Official explanation :
class Solution {
public:
int quickSelect(vector<int>& a, int l, int r, int index) {
int q = randomPartition(a, l, r);
if (q == index) {
return a[q];
} else {
return q < index ? quickSelect(a, q + 1, r, index) : quickSelect(a, l, q - 1, index);
}
}
inline int randomPartition(vector<int>& a, int l, int r) {
int i = rand() % (r - l + 1) + l;
swap(a[i], a[r]);
return partition(a, l, r);
}
inline int partition(vector<int>& a, int l, int r) {
int x = a[r], i = l - 1;
for (int j = l; j < r; ++j) {
if (a[j] <= x) {
swap(a[++i], a[j]);
}
}
swap(a[i + 1], a[r]);
return i + 1;
}
int findKthLargest(vector<int>& nums, int k) {
srand(time(0));
return quickSelect(nums, 0, nums.size() - 1, nums.size() - k);
}
};
my ( recursive ):
class Solution {
int Partition(vector<int>& nums, int l, int r){
// Scramble the array , Take the middle of three numbers
int mid = l+(r-l)/2;
if(nums[l] > nums[r]) swap(nums[l], nums[r]);
if(nums[mid] > nums[r]) swap(nums[mid], nums[r]);
if(nums[mid] > nums[l]) swap(nums[mid], nums[l]);
// here nums[l] Is the median of three numbers
int privot = nums[l]; // Select the first as the pivot
while(l < r){
while(l < r && nums[r] <= privot)
r--;
nums[l] = nums[r];
while(l < r && nums[l] >= privot)
l++;
nums[r] = nums[l];
}
nums[l] = privot;
return l;
}
void Quicksort(vector<int>& nums, int l, int r){
if(l < r){
int privot = Partition(nums, l, r); // Get pivot
Quicksort(nums, l, privot-1);
Quicksort(nums, privot+1, r);
}
}
public:
int findKthLargest(vector<int>& nums, int k) {
if(nums.size() == 1) return nums[0];
// Quick sort
Quicksort(nums, 0, nums.size()-1);
return nums[k-1];
}
};
Complexity analysis
Time complexity :Leetcode The time complexity of the official solution is O ( n ) O(n) O(n). The average time complexity of conventional quick sort is O ( n log n ) O(n \log n) O(nlogn).
Spatial complexity : O ( log n ) O(\log n) O(logn), The expected space cost of recursively using stack space is O ( log n ) O(\log n) O(logn).
Methods seven : Heap sort
Ideas
Build a big top pile , Then delete k − 1 k-1 k−1 A heap top element , Then the heap top element at this time is k k k Big elements .
Code implementation
Leetcode Official explanation :
class Solution {
public:
void maxHeapify(vector<int>& a, int i, int heapSize) {
int l = i * 2 + 1, r = i * 2 + 2, largest = i;
if (l < heapSize && a[l] > a[largest]) {
largest = l;
}
if (r < heapSize && a[r] > a[largest]) {
largest = r;
}
if (largest != i) {
swap(a[i], a[largest]);
maxHeapify(a, largest, heapSize);
}
}
void buildMaxHeap(vector<int>& a, int heapSize) {
for (int i = heapSize / 2; i >= 0; --i) {
maxHeapify(a, i, heapSize);
}
}
int findKthLargest(vector<int>& nums, int k) {
int heapSize = nums.size();
buildMaxHeap(nums, heapSize);
for (int i = nums.size() - 1; i >= nums.size() - k + 1; --i) {
swap(nums[0], nums[i]);
--heapSize;
maxHeapify(nums, 0, heapSize);
}
return nums[0];
}
};
Complexity analysis
Time complexity : O ( n log n ) O(n \log n) O(nlogn), The time cost of building the reactor is O ( n ) O(n) O(n), The total cost of deletion is O ( k log n ) O(k \log n) O(klogn), because k < n k < n k<n, Therefore, the asymptotic time is complex O ( n + k log n ) O(n + k \log n) O(n+klogn) Simplify O ( n log n ) O(n \log n) O(nlogn).
Spatial complexity : O ( log n ) O(\log n) O(logn), That is, the space cost of recursive writing using stack space .
边栏推荐
- Why does the producer / consumer mode wait () use while instead of if (clear and understandable)
- Text processing function sorting in mysql, quick search of collection
- [MySQL transaction]
- Redis - detailed explanation of cache avalanche, cache penetration and cache breakdown
- This article is enough for learning advanced mysql
- Zephyr 學習筆記2,Scheduling
- Transition technology from IPv4 to IPv6
- SQL foundation 9 [grouping data]
- Write a thread pool by hand, and take you to learn the implementation principle of ThreadPoolExecutor thread pool
- Introduction to sap commerce cloud B2B organization function
猜你喜欢
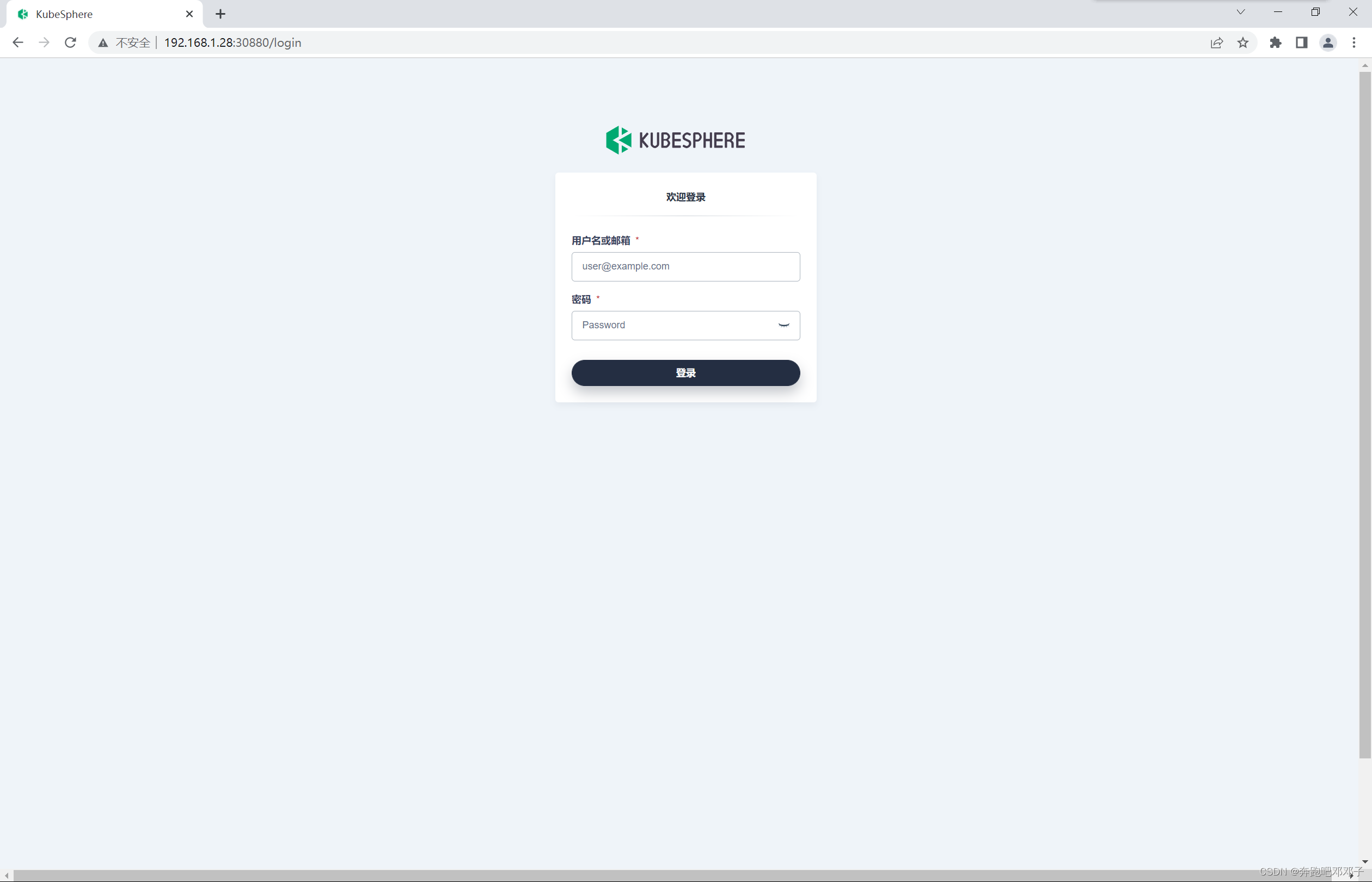
【Kubernetes系列】Kubernetes 上安装 KubeSphere
How to send mail with Jianmu Ci
Take you to master the formatter of visual studio code
![SQL foundation 9 [grouping data]](/img/8a/a72941d8c3413316b063033a1b5038.jpg)
SQL foundation 9 [grouping data]
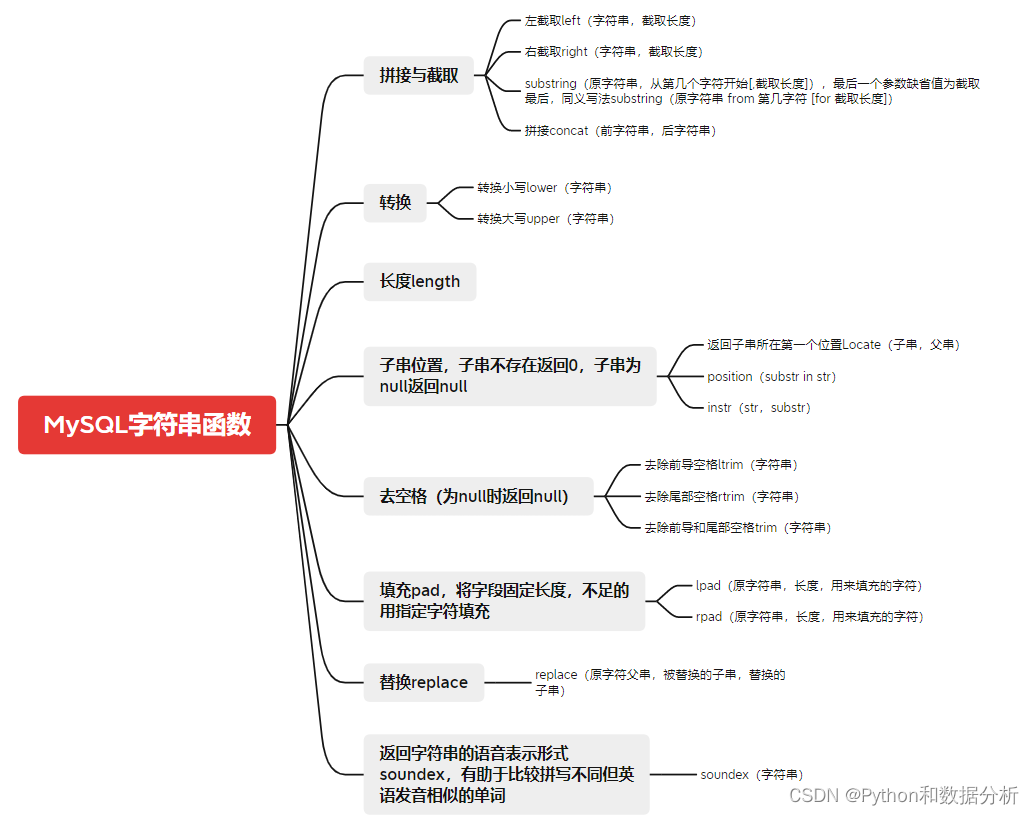
Tri des fonctions de traitement de texte dans MySQL, recherche rapide préférée
![[C language] open the door of C](/img/e0/2f107966423d6492c39995c77a445e.jpg)
[C language] open the door of C

两年前美国芯片扭捏着不卖芯片,如今芯片堆积如山祈求中国帮忙

tornado项目之路由装饰器
Comparison between applet framework and platform compilation

It's healthy to drink medicinal wine like this. Are you drinking it right
随机推荐
BUUCTF(3)
Oceanbase is the leader in the magic quadrant of China's database in 2021
在所有SwiftUI版本(1.0-4.0)中原生实现Charts图表视图之思路
Electronic Association C language level 1 34, piecewise function
【FreeRTOS】FreeRTOS学习笔记(7)— 手写FreeRTOS双向链表/源码分析
大学阶段总结
Handwritten easy version flexible JS and source code analysis
How does dataframe calculate the average value of each row as another column
[Chongqing Guangdong education] National Open University spring 2019 770 real estate appraisal reference questions
[Mori city] random talk on GIS data (I)
Text processing function sorting in mysql, quick search of collection
One of the general document service practice series
Is l1-029 too fat (5 points)
Book list | as the technical support Party of the Winter Olympics, Alibaba cloud's technology is written in these books!
【Kubernetes系列】Kubernetes 上安装 KubeSphere
[web security] nodejs prototype chain pollution analysis
L2-013 red alarm (C language) and relevant knowledge of parallel search
When JDBC connects to es query, is there a God who meets the following situation?
MYCAT middleware installation and use
论文学习——基于极值点特征的时间序列相似性查询方法