当前位置:网站首页>Introduction to robotics I. spatial transformation (1) posture, transformation
Introduction to robotics I. spatial transformation (1) posture, transformation
2022-07-06 00:52:00 【RuiH. AI】
Introduction to Robotics One 、 Spatial transformation (1) Postures
Preface
Due to the close relationship between visual servo and manipulator , Therefore, we should start from the foundation , Record the robot kinematics .
This paper records the position and posture of rigid bodies . actually , Spatial transformation in SLAM It has been mentioned once in the column , However, the introduction to robotics gives a more detailed description of rigid body motion .
Coordinate system
There are usually two coordinate systems , One is the world coordinate system for reference ( Cartesian coordinate system ), One is the rigid body coordinate system with the center of mass of the rigid body as the origin .
The robot coordinate system follows the right-hand rule , As shown in the figure below 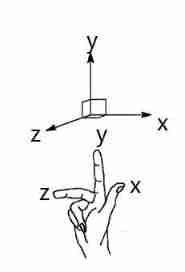
Postures
Posture is position and posture , Corresponding displacement and rotation . The position and posture of the robot must be referred to the world coordinate system .
Posture represents the relationship between reference systems .
Location
The position of the rigid body is represented by a vector .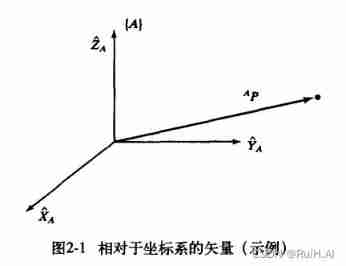
There is a point in the figure above P P P, In a coordinate system { A } \{A\} { A} For reference , You can put the vector O P OP OP To express A P ^AP AP The location of , Its left superscript indicates the reference system . A P ^AP AP The coordinates of are expressed as :
A P = [ p x , p y , p z ] T ^AP = [p_x,p_y,p_z]^T AP=[px,py,pz]T
Posture
The attitude of the rigid body is represented by the unit vector of the three principal axes of the rigid body coordinate system in the reference system .
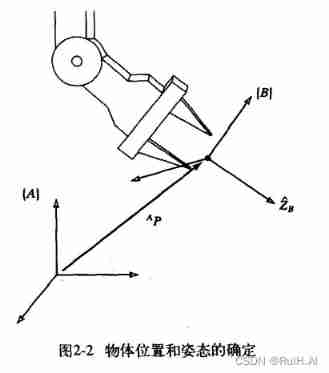
Above picture , X ^ B , Y ^ B , Z ^ B \hat X_B,\hat Y_B, \hat Z_B X^B,Y^B,Z^B Represents the unit vector of the three principal axes of the rigid body in the upper right corner , They are in the frame of reference { A } \{A\} { A} The expression of in is A X ^ B , A Y ^ B , A Z ^ B ^A\hat X_B, ^A\hat Y_B, ^A\hat Z_B AX^B,AY^B,AZ^B. These three unit vectors form the rotation matrix :
B A R = ( A X ^ B A Y ^ B A Z ^ B ) ^A_BR=(^A\hat X_B \quad ^A\hat Y_B \quad ^A\hat Z_B) BAR=(AX^BAY^BAZ^B)
So how to calculate the coordinates of the principal axis unit vector of the rigid body in the reference system ?
With A X ^ B ^A\hat X_B AX^B For example , Its x The value of the coordinate is actually A X ^ B ^A\hat X_B AX^B In the frame of reference X The projection on the axis ,y, z The coordinates are in the reference system Y, Z The projection on the axis :
B A R = ( A X ^ B A Y ^ B A Z ^ B ) = [ X ^ B ⋅ X ^ A Y ^ B ⋅ X ^ A Z ^ B ⋅ X ^ A X ^ B ⋅ Y ^ A Y ^ B ⋅ Y ^ A Z ^ B ⋅ Y ^ A X ^ B ⋅ Z ^ A Y ^ B ⋅ Y ^ A Z ^ B ⋅ X ^ A ] ^A_BR=(^A\hat X_B \quad ^A\hat Y_B \quad ^A\hat Z_B) = \begin{bmatrix} \hat X_B \cdot \hat X_A & \hat Y_B \cdot \hat X_A & \hat Z_B \cdot \hat X_A\\ \hat X_B \cdot \hat Y_A & \hat Y_B \cdot \hat Y_A & \hat Z_B \cdot \hat Y_A\\ \hat X_B \cdot \hat Z_A & \hat Y_B \cdot \hat Y_A & \hat Z_B \cdot \hat X_A\\ \end{bmatrix} BAR=(AX^BAY^BAZ^B)=⎣⎡X^B⋅X^AX^B⋅Y^AX^B⋅Z^AY^B⋅X^AY^B⋅Y^AY^B⋅Y^AZ^B⋅X^AZ^B⋅Y^AZ^B⋅X^A⎦⎤
The rotation matrix is an orthogonal matrix , The proof is simple :
B A R T B A R = [ A X ^ B T A Y ^ B T A Z ^ B T ] ( A X ^ B A Y ^ B A Z ^ B ) = I 3 ^A_BR^T\ ^A_B R= \begin{bmatrix} ^A\hat X^T_B \\ ^A\hat Y^T_B \\ ^A\hat Z^T_B \end{bmatrix} (^A\hat X_B \quad ^A\hat Y_B \quad ^A\hat Z_B) = I_3 BART BAR=⎣⎡AX^BTAY^BTAZ^BT⎦⎤(AX^BAY^BAZ^B)=I3
The inner product of the unit vector in the same direction is 1, The inner product of mutually perpendicular unit vectors is 0, therefore A X ^ B T A X ^ B = 1 , A X ^ B T A Y ^ B = 0 ^A\hat X^T_B \ ^A\hat X_B=1, ^A\hat X^T_B \ ^A\hat Y_B=0 AX^BT AX^B=1,AX^BT AY^B=0, So we can get the identity matrix above .
Pose transformation
Pose transformation refers to the change of the position and pose of the rigid body coordinate system , Translation and rotation , Get the relative pose between the rigid system and the reference system
Still in order to 2-2 For example , The pose transformation of rigid body coordinate system relative to reference system can be expressed as :
{ B A R , A P B O R G } \{^A_B R, \ ^AP_{BORG} \} { BAR, APBORG}
That is to say SLAM In the fourteenth lecture R , t R,t R,t
mapping
Mapping represents the coordinate transformation of the same point between different coordinate systems .
Mapping includes translation and rotation .
translation
Translation is related to the position of the origin of the rigid body coordinate system .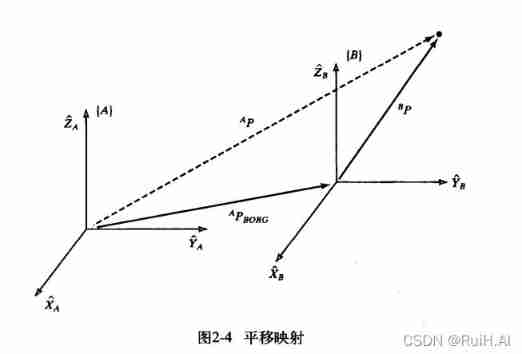
Above picture , It is known that B P ^BP BP Indication point P In the coordinate system { B } \{B\} { B} Position in , A P B O R G ^AP_{BORG} APBORG Expressed in the reference system { A } \{A\} { A} Next { B } \{B\} { B} The position of the origin . be A P ^AP AP Can be expressed as :
A P = B P + A P B O R G ^AP= \ ^BP + \ ^AP_{BORG} AP= BP+ APBORG
Only when the attitude of the two coordinate systems is the same , To perform the above translation .
rotate
Rotation is related to the attitude of the rigid body coordinate system .
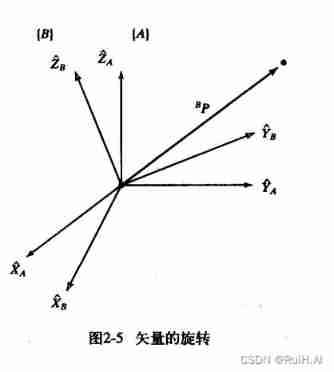
Above picture , It is known that B P ^BP BP Indication point P In the coordinate system { B } \{B\} { B} Position in . A P ^AP AP Expressed in the reference system { A } \{A\} { A} The next position , Vector A P ^AP AP In the direction of the principal axis of the reference system X ^ A , Y ^ A , Z ^ A \hat X_A, \hat Y_A, \hat Z_A X^A,Y^A,Z^A The projection of ( Unit vector inner product ). Besides , We know , The inner product of a vector needs to be expressed in the same coordinate system to be meaningful . be A P ^AP AP Can be expressed as :
A P = [ B X ^ A ⋅ B P B Y ^ A ⋅ B P B Z ^ A ⋅ B P ] = B A R B P ^AP= \begin{bmatrix} ^B \hat X_A \cdot\ ^BP & ^B \hat Y_A \cdot\ ^BP & ^B \hat Z_A \cdot\ ^BP \end{bmatrix} = \ ^A_BR \ ^BP AP=[BX^A⋅ BPBY^A⋅ BPBZ^A⋅ BP]= BAR BP
Transformation
Transformation = Spin first , Back translation .
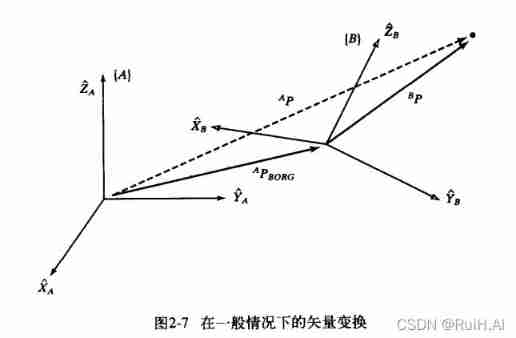
Above picture , Need to use B P ^BP BP Express A P ^AP AP. First of all, will B P ^BP BP Map to an intermediate coordinate system { B ′ } \{B'\} { B′}, The attitude of this coordinate system is consistent with { A } \{A\} { A} identical , Origin and { B } \{B\} { B} identical . And then use B ′ P ^{B'}P B′P Express A P ^AP AP:
A P = B ′ P + A P B ′ O R G = B B ′ R B P + A P B ′ O R G = B A R B P + A P B O R G ^AP = \ ^{B'}P + \ ^AP_{B'ORG} = \ ^{B'}_BR \ ^BP + \ ^AP_{B'ORG} = \ ^{A}_BR \ ^BP + \ ^AP_{BORG} AP= B′P+ APB′ORG= BB′R BP+ APB′ORG= BAR BP+ APBORG
It corresponds to SLAM In the fourteenth lecture P ′ = R P + t P'=RP+t P′=RP+t
Introduce homogeneous matrix , There is the concept of transformation matrix :
[ A P 1 ] = [ B A R A P B O R G 0 1 ] [ B P 1 ] A P = B A T B P \begin{bmatrix} ^AP \\ 1 \\ \end{bmatrix} = \begin{bmatrix} \ ^A_BR & ^AP_{BORG} \\ {\bf 0} & 1 \\ \end{bmatrix} \begin{bmatrix} \ ^BP \\ 1 \\ \end{bmatrix} \\ \quad \\ \\ \quad \\ ^AP = \ ^A_BT \ ^BP [AP1]=[ BAR0APBORG1][ BP1]AP= BAT BP
Composite transformation
If known B A T , C B T ^A_B T, \ ^B_CT BAT, CBT, You can use the C P ^CP CP Express A P ^AP AP:
A P = B A T C B T C P ^AP = ^A_BT \ ^B_CT \ ^CP AP=BAT CBT CP
inverse transformation
Inverse of rotation matrix :
B A R = A B R T ^A_B R = \ ^B_AR^T BAR= ABRT
Inverse of transformation matrix :
[ B A R T − B A R T A P B O R G 0 1 ] \begin{bmatrix} \ ^A_BR^T & -^A_BR^T\ ^AP_{BORG} \\ {\bf 0} & 1 \\ \end{bmatrix} [ BART0−BART APBORG1]
There are two ways to find the inverse of a transformation matrix , One is to find the inverse of the matrix directly ; The other is to find the inverse through the transformation property . Introduce the latter .

If known A P ^AP AP seek B P ^BP BP, Yes :
B P = A B R A P + B P A O R G ^BP = \ ^B_AR \ ^AP + \ ^BP_{AORG} BP= ABR AP+ BPAORG
If A P ^AP AP yes { B } \{B\} { B} The origin of , namely :
0 = B P B O R G = A B R A P B O R G + B P A O R G B P A O R G = − A B R A P B O R G = − B A R T A P B O R G B P = B A R T A P − B A R T A P B O R G {\bf 0} = ^BP_{BORG} = ^B_AR \ ^AP_{BORG} + \ ^BP_{AORG} \\ \quad \\ \ ^BP_{AORG} = - ^B_AR \ ^AP_{BORG} = -^A_BR^T \ ^AP_{BORG} \\ \quad \\ \ ^BP = \ ^A_BR^T \ ^AP - \ ^A_BR^T \ ^AP_{BORG} 0=BPBORG=ABR APBORG+ BPAORG BPAORG=−ABR APBORG=−BART APBORG BP= BART AP− BART APBORG
Postscript
This article is actually SLAM The clearer expression method of posture transformation in Lecture 14 , The reference system is placed on the left superscript .
边栏推荐
- [groovy] compile time meta programming (compile time method interception | method interception in myasttransformation visit method)
- Cloud guide DNS, knowledge popularization and classroom notes
- Problems and solutions of converting date into specified string in date class
- Keepalive component cache does not take effect
- Natural language processing (NLP) - third party Library (Toolkit):allenlp [library for building various NLP models; based on pytorch]
- Why can't mathematics give machine consciousness
- [groovy] compile time meta programming (AST syntax tree conversion with annotations | define annotations and use groovyasttransformationclass to indicate ast conversion interface | ast conversion inte
- Yolov5, pychar, Anaconda environment installation
- Kotlin core programming - algebraic data types and pattern matching (3)
- How spark gets columns in dataframe --column, $, column, apply
猜你喜欢

2020.2.13

Folding and sinking sand -- weekly record of ETF
The relationship between FPGA internal hardware structure and code
I'm interested in watching Tiktok live beyond concert
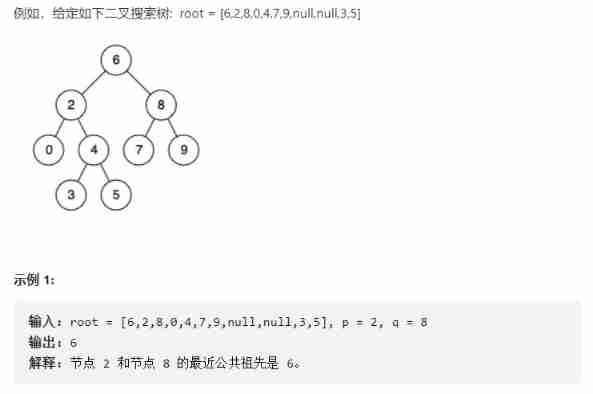
Finding the nearest common ancestor of binary search tree by recursion

What is the most suitable book for programmers to engage in open source?
![Cf:d. insert a progression [about the insert in the array + the nature of absolute value + greedy top-down]](/img/9e/c933f454a39d906a407e4d415f0b87.png)
Cf:d. insert a progression [about the insert in the array + the nature of absolute value + greedy top-down]
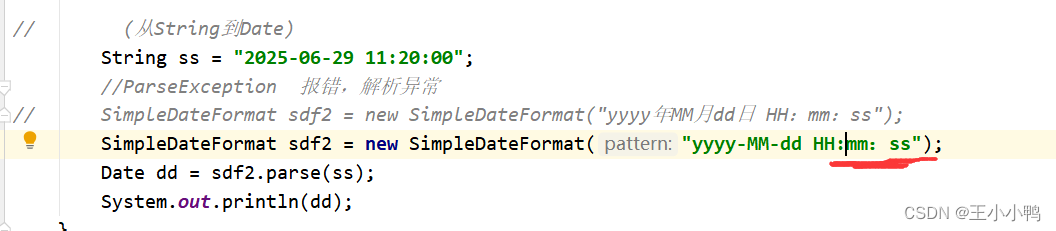
Problems and solutions of converting date into specified string in date class

Arduino六足机器人
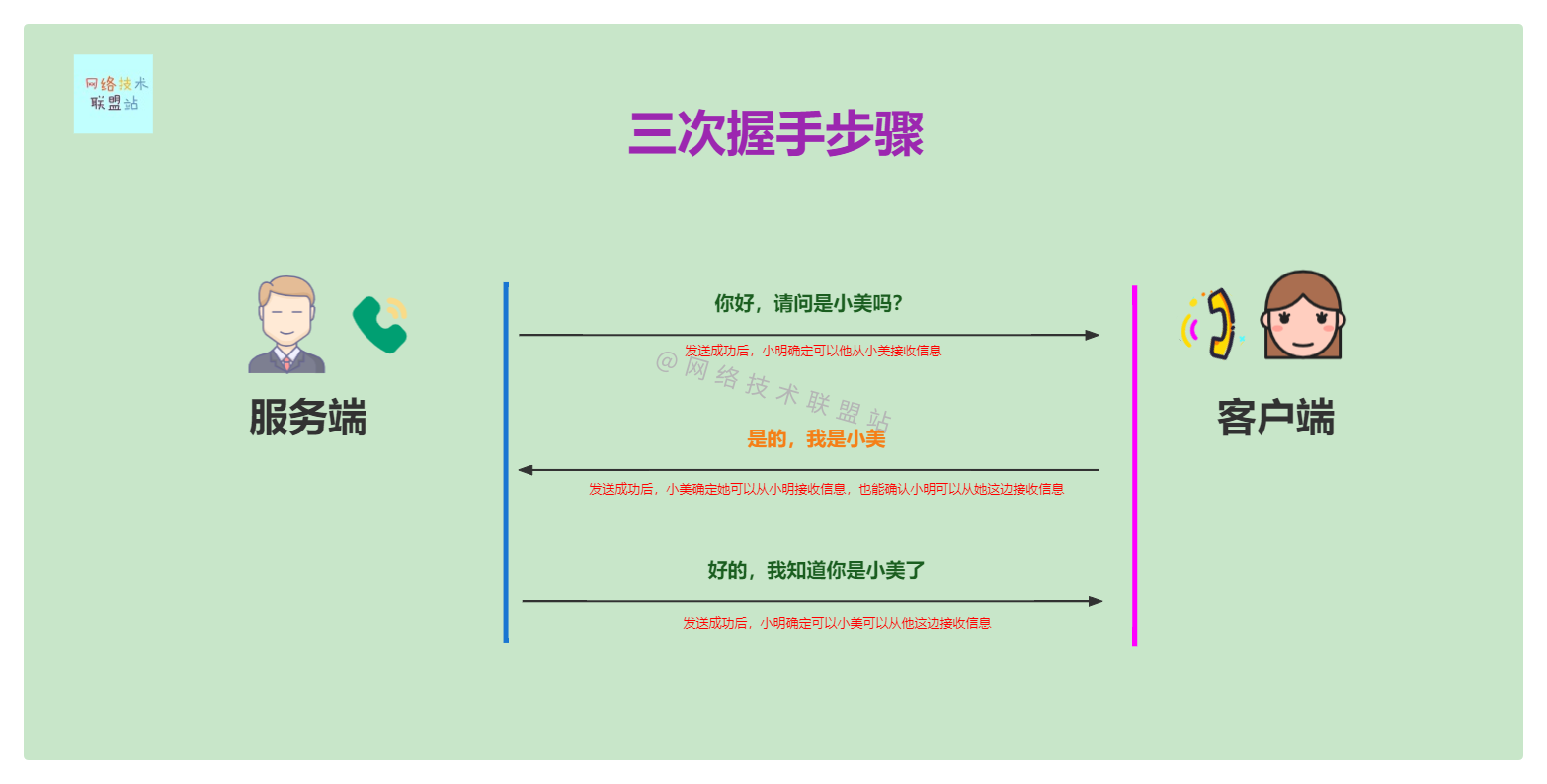
Illustrated network: the principle behind TCP three-time handshake, why can't two-time handshake?
随机推荐
程序员成长第九篇:真实项目中的注意事项
Starting from 1.5, build a micro Service Framework - call chain tracking traceid
Free chat robot API
Beginner redis
NLP text processing: lemma [English] [put the deformation of various types of words into one form] [wet- > go; are- > be]
[groovy] compile time metaprogramming (compile time method interception | find the method to be intercepted in the myasttransformation visit method)
After 95, the CV engineer posted the payroll and made up this. It's really fragrant
vSphere实现虚拟机迁移
【EI会议分享】2022年第三届智能制造与自动化前沿国际会议(CFIMA 2022)
面试必刷算法TOP101之回溯篇 TOP34
KDD 2022 | 脑电AI助力癫痫疾病诊断
The detailed page returns to the list and retains the original position of the scroll bar
关于#数据库#的问题:(5)查询库存表中每本书的条码、位置和借阅的读者编号
【文件IO的简单实现】
[EI conference sharing] the Third International Conference on intelligent manufacturing and automation frontier in 2022 (cfima 2022)
Uniapp development, packaged as H5 and deployed to the server
How spark gets columns in dataframe --column, $, column, apply
Extension and application of timestamp
ubantu 查看cudnn和cuda的版本
【线上小工具】开发过程中会用到的线上小工具合集