当前位置:网站首页>二叉树的遍历:递归法/ 迭代法/ 统一迭代法(强QAQ)
二叉树的遍历:递归法/ 迭代法/ 统一迭代法(强QAQ)
2022-08-02 14:10:00 【鱼子酱:P】
最近刷题刷到二叉树...算法面试的常客,数据结构基石...
见到许多厉害的解法,膜拜啊~
特此记录一下2022/3/24
力扣对应题目:144,145,94
一:递归法
一看就会,一写就废!~简单解法
前序遍历:
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> result = new ArrayList<Integer>();
preorder(root, result);
return result;
}
public void preorder(TreeNode root, List<Integer> result) {
if (root == null) {
return;
}
result.add(root.val);
preorder(root.left, result);
preorder(root.right, result);
}
}中序遍历:
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
inorder(root, res);
return res;
}
void inorder(TreeNode root, List<Integer> list) {
if (root == null) {
return;
}
inorder(root.left, list);
list.add(root.val); // 注意这一句
inorder(root.right, list);
}
}后序遍历:
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
postorder(root, res);
return res;
}
void postorder(TreeNode root, List<Integer> list) {
if (root == null) {
return;
}
postorder(root.left, list);
postorder(root.right, list);
list.add(root.val); // 注意这一句
}
}二:迭代法
递归的实现就是:每一次递归调用都会把函数的局部变量、参数值和返回地址等压入调用栈中,然后递归返回的时候,从栈顶弹出上一次递归的各项参数,所以这就是递归为什么可以返回上一层位置的原因。so 可以用栈!
前序遍历:
// 前序遍历顺序:中-左-右,入栈顺序:中-右-左
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> result = new ArrayList<>();
if (root == null){
return result;
}
Stack<TreeNode> stack = new Stack<>();
stack.push(root);
while (!stack.isEmpty()){
TreeNode node = stack.pop();
result.add(node.val);
if (node.right != null){
stack.push(node.right);
}
if (node.left != null){
stack.push(node.left);
}
}
return result;
}
}中序遍历:
lass Solution {
public List<Integer> inorderTraversal(TreeNode root) {
//中序遍历:左中右 入栈顺序:左右
List<Integer> result = new ArrayList<>();
if (root == null){
return result;
}
Stack<TreeNode> stack = new Stack<>();
TreeNode cur = root;
while (cur != null || !stack.isEmpty()){
if (cur != null){
stack.push(cur);//头结点入栈
cur = cur.left;//一直遍历放左节点,到最左的叶子结点,然后到else取出最左的结点,然后放右结点。左边-中间-右边
}else{
cur = stack.pop();
result.add(cur.val);
cur = cur.right;
}
}
return result;
}
}后续遍历:
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
//左右中 入栈顺序:中左右 出栈顺序:中右左 翻转:左右中
List<Integer> res = new ArrayList<>();
if(root == null){
return res;
}
Stack<TreeNode> stack1 = new Stack<>();
stack1.push(root);//头结点入栈
while(!stack1.isEmpty()){
TreeNode node = stack1.pop();
res.add(node.val);
if(node.left != null){
stack1.push(node.left);
}
if(node.right != null){
stack1.push(node.right);
}
}
Collections.reverse(res);
return res;
}
}三:统一迭代法
迭代法实现的先中后序,其实风格也不是那么统一,除了先序和后序,有关联,中序完全就是另一个风格了,一会用栈遍历,一会又用指针来遍历。
其实针对三种遍历方式,使用迭代法是可以写出统一风格的代码!
重头戏来了,接下来介绍一下统一写法。
用栈的话,无法同时解决访问节点(遍历节点)和处理节点(将元素放进结果集)不一致的情况。那我们就将访问的节点放入栈中,把要处理的节点也放入栈中但是要做标记。如何标记呢,就是要处理的节点放入栈之后,紧接着放入一个空指针作为标记。 这种方法也可以叫做标记法。
前序遍历:
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
//前序:中左右 入栈顺序:右左中
List<Integer> res = new ArrayList<>();//LinkedList也可以
Stack<TreeNode> st = new Stack<>();
if(root != null) st.push(root);
while(!st.empty()){
TreeNode node = st.peek();
if(node != null){
st.pop();//把该节点弹出,避免重复操作
if(node.right != null) st.push(node.right);
if(node.left != null) st.push(node.left);
st.push(node);
st.push(null);//中间结点访问过,但还没有处理,加入空节点标记
}else{
st.pop();//弹出空节点
node = st.pop();//取出被标记的结点
res.add(node.val);//加入res中
}
}
return res;
}
}中序遍历:
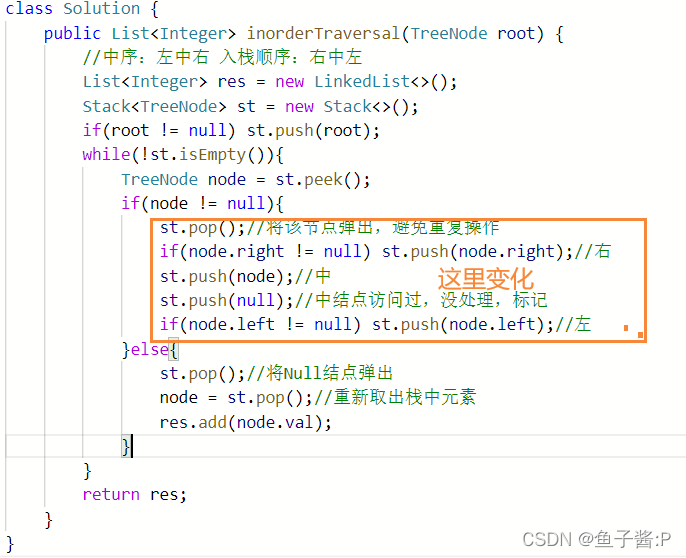
后续遍历:
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
//后序:左右中 入栈顺序:中右左
List<Integer> res = new LinkedList<>();
Stack<TreeNode> st = new Stack<>();
if(root != null ) st.push(root);
while(!st.empty()){
TreeNode node = st.peek();
if(node != null){
st.pop();//弹出该节点,避免重复
st.push(node);
st.push(null);//中方结点访问过,没处理,标记
if(node.right != null) st.push(node.right);
if(node.left != null) st.push(node.left);
}else{
st.pop();//把null结点弹出
node = st.pop();
res.add(node.val);
}
}
return res;
}
}边栏推荐
- DP4344兼容CS4344-DA转换器
- Open the door of power and electricity "Circuit" (2): Power Calculation and Judgment
- 基于最小二乘法的线性回归分析方程中系数的估计
- Mysql connection error solution
- 7. How to add the Click to RecyclerView and LongClick events
- 关于c语言的调试技巧
- Installation and configuration of Spark and related ecological components - quick recall
- Win10电脑需要安装杀毒软件吗?
- Publish module to NPM should be how to operate?Solutions to problems and mistake
- 推开机电的大门《电路》(一):电压,电流,参考方向
猜你喜欢
Installation and configuration of Spark and related ecological components - quick recall
Yolov5 official code reading - prior to transmission
Win10无法连接打印机怎么办?不能使用打印机的解决方法

3.用户上传头像
Win11 keeps popping up User Account Control how to fix it
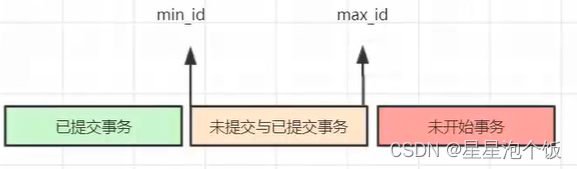
Mysql之MVCC
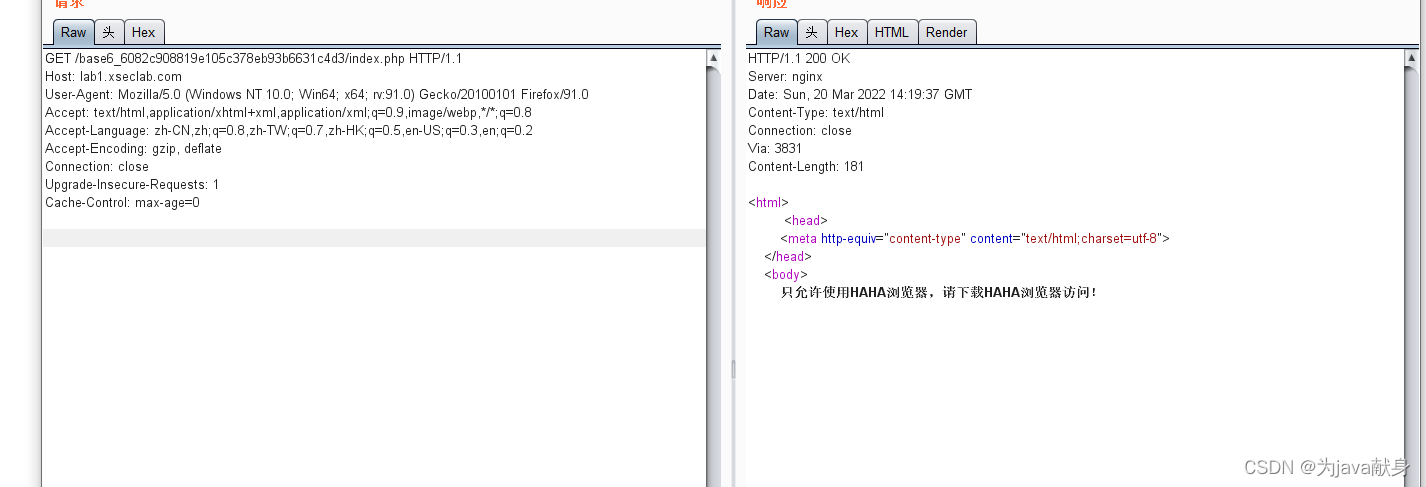
网络安全抓包
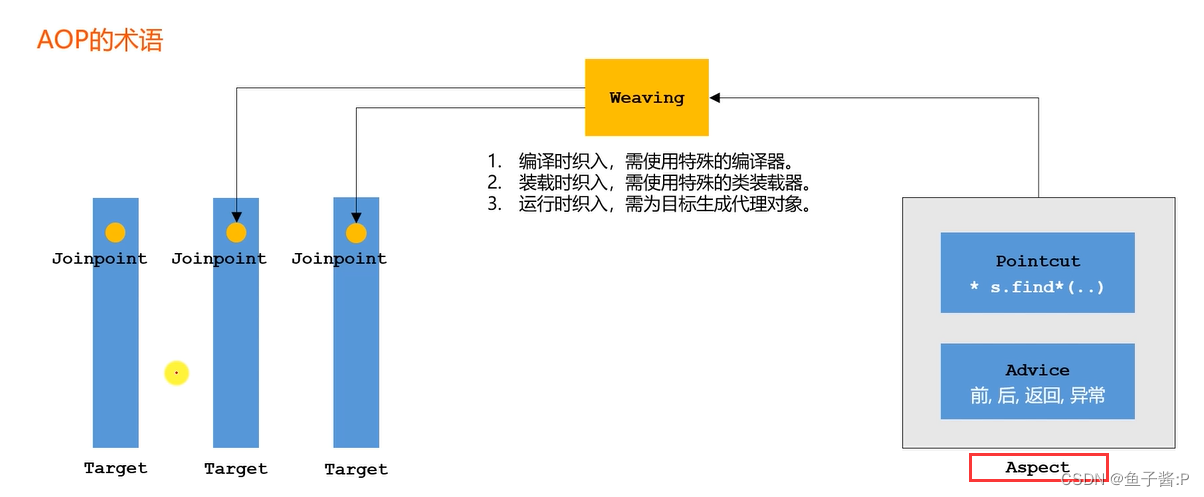
6.统一记录日志
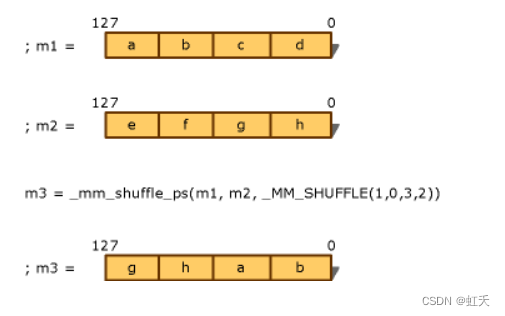
The SSE instructions into ARM NEON
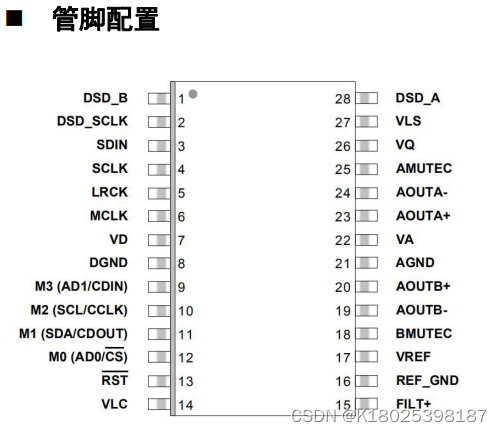
CS4398音频解码替代芯片DP4398完全兼容DAC解码
随机推荐
DP1101兼容CC1101是SUB1GHz无线收发芯片应用于智能家居
flink+sklearn——使用jpmml实现flink上的机器学习模型部署
Do Windows 10 computers need antivirus software installed?
为vscode配置clangd
动态规划理论篇
Win10 cannot directly use photo viewer to open the picture
LeetCode2 电话号码的字母组合
win10 system update error code 0x80244022 how to do
Win10 computer can't read U disk?Don't recognize U disk how to solve?
golang之GMP调度模型
实战美团Nuxt +Vue全家桶,服务端渲染,邮箱验证,passport鉴权服务,地图API引用,mongodb,redis等技术点
FP7126降压恒流65536级高辉无频闪调光共阳极舞台灯RGB驱动方案
Win10 Settings screen out from lack of sleep?Win10 set the method that never sleep
Codeforces Round #605 (Div. 3)
Compilation error D8021: Invalid numeric argument '/Wextra' cl command line error d8021 invalid numeric argument '/Wextra'
win11一直弹出用户账户控制怎么解决
日常-笔记
使用libcurl将Opencv Mat的图像上传到文件服务器,基于post请求和ftp协议两种方法
How to set the win10 taskbar does not merge icons
Open the door to electricity "Circuit" (3): Talk about different resistance and conductance