当前位置:网站首页>第二十九章:树的基本概念和性质
第二十九章:树的基本概念和性质
2022-08-02 14:10:00 【WANGHAOXIN364】
之前学习了数组、字符串、队列、栈等等数据类型和数据结构,它们都是线性存储结构。本章要学习的树结构是一种非线性存储结构,存储的是具有“一对多”关系的数据元素的集合。
树结构不论是在竞赛中,还是在实际的工程开发中,都是一类重要的非线性数据结构,树中的节点之间具有明确的层次关系,并且每个节点会“分支”出若干个其他节点。
数据结构中的树和现实生活中的树长得一样,只不过我们习惯于处理问题的时候把树根放到上方来考虑。这种数据结构看起来像是一个倒挂的树,因此得名。后面我们提到的树均指数据结构中的树。

数据结构中的树和实际生活中的树的模型
学习目标:
- 掌握树的相关的概念;
- 掌握树的性质;
- 对于具体问题,能够分析问题并判断问题中的数据能否用树结构表示。
一、树的定义
树的定义
树(Tree)是由 n(n≥0)n(n≥0) 个结点组成的一个非线性、具有层次关系的集合。(特别地,当 n = 0n=0 时,称树为空树,这是一种特殊情况)
树可以分为有根树和无根树两种:
- 有根树:有一个确定的根节点;
- 无根树:根不确定,任何结点都可以作为树的根;
无根树
无根树主要在后面将会学习的图论算法中的出现,不是现阶段学习的重点。
一个没有固定根结点的树称为无根树(unrooted tree)。无根树有几种等价的形式化定义:
- 有 nn 个结点, n-1n−1 条边的连通无向图
- 无向无环的连通图
- 任意两个结点之间有且仅有一条简单路径的无向图
- 任何边均为桥的连通图
- 没有圈,且在任意不同两点间添加一条边之后所得图含唯一的一个圈的图
无根树的例子也很多,例如 nn 个城市被 n-1n−1 条公里连在一起,如果将城市看作点,将公路看作边,那整个城市公路网络就是一棵树,因为没有明确的根结点,因此它是一棵无根树。

有根树
有根树相对于无根树,有很多特有的概念,请一定要注意区分二者。在处理问题时,要弄清楚问题模型中的树是哪一种。
在无根树的基础上,指定一个结点称为根 ,则形成一棵有根树 (rooted tree)。有根树在很多时候仍以无向图表示,只是规定了结点之间的上下层级关系。
对于有根树,必须明确树的 根。树根是整棵树的起点,从树根开始,通过树枝(称为 树边)向下可以逐步扩展出很多其他的 子结点,其中有些子结点还能继续向下扩展延伸,这些节点成为树的 分支节点。有些子结点不能再向下扩展了,我们称之为树的 叶子结点或简称 叶结点。
二、树的概念
除了根结点、叶子结点、树边等概念外,还有如下一些概念:
1、适用于无根树和有根树的概念
以下概念同时适用于无根树和有根树
- 森林(forest) : 由 m(m≥0)m(m≥0) 棵互不相交的树构成的集合。按照定义,一棵树也是森林。
- 生成树(spanning tree) :一个连通无向图的生成子图,同时要求是树。也即在有 nn 个节点的图的边集中选择 n - 1n−1 条,将所有顶点连通。
无根树的叶结点(leaf node) :度数不超过 1 的结点。(为什么是“不超过 1”,而不是“恰为 1” ?考虑树只有一个结点时,没有其他节点。)
有根树的叶结点(leaf node) :没有子结点的结点。

<center>森林的概念</center>
2、只适用于有根树的概念
以下概念只适用于有根树
祖先(ancestor) :一个结点到根结点的路径上,除了它本身外的结点构成的集合。根结点的祖先集合为空。
父结点(parent node) :对于除根以外的每个结点,定义为从该结点到根路径上的第二个结点。 注意:**根结点没有父结点**。(有的教材里也称之为父亲结点或双亲结点)
子结点(child node) :如果 uu 是 vv 的父亲,那么 vv 是 uu 的子结点(孩子)。子结点的顺序一般不加以区分,二叉树是一个例外。
兄弟(sibling) :同一个父亲的多个子结点互为兄弟。
堂兄弟:同一层次的所有不互为兄弟的结点互为堂兄弟。
后代(descendant) :子结点和子结点的后代。或者理解成:如果 uu 是 vv 的祖先,那么 vv 是 uu 的后代。
结点的度:结点儿子的个数,称为结点的度。显然,叶子结点的度为 0。
结点的高度(depth) :也称结点的层次或深度,指到根结点的路径上的边数。根节点的高度为 0,根的子结点高度为 1,以此类推。 注意:也有一些场合为了方便会把根结点的高度定义为 1。
树的高度(height) :也称树的深度,所有结点的深度的最大值。
树的度:树中结点的最大度数称为树的度。
子树(subtree) :删掉与父亲相连的边后,该结点所在的子图。
问:结点的深度和高度的区别?
答:深度是从根结点开始**自顶向下**逐层累加的,高度是从叶结点开始**自底向上**逐层累加的。

3、一些特殊的树
以下这些树很特殊,在思考和解决问题时,应注意算法和代码在以下特殊情况下会发生什么。有些时候,问题会考察这些特殊情况。
- 链(chain/path graph) :满足与任一结点相连的边不超过 22 条的树称为链。**一个有 nn 个结点的树,当它是链树时,树的高度最大,达到 n-1n−1。**
- 菊花/星星(star) :满足存在 uu 使得所有除 uu 以外结点均与 uu 相连的树称为菊花。**一个有 n(n\geq 2)n(n≥2) 个结点的树,当它是链树时,树的高度最小,为 11。**
- 有根二叉树(rooted binary tree) :每个结点最多只有两个儿子(子结点)的有根树称为二叉树。常常对两个子结点的顺序加以区分,分别称之为左子结点和右子结点。大多数情况下, 二叉树 一词均指有根二叉树。

三、树的性质
(1)对于有根树,除根节点外,其余结点有且仅有一个父结点,即 根结点没有父结点。
(2)nn 个结点的树中有且仅有 n-1n−1 条边;
(3)树是不存在环的连通图;
(4)树中任意两个结点之间有且仅有一条简单路径;
(5)树中的结点数等于所有结点的度数加 1;
(6)度为 kk 的树中第 ii 层上至多有 k^{i}ki 个结点(根节点为第 1 层);
(7)高度为 hh (根节点高度为 1)的 kk 叉树最多有 (k^h-1)/(k-1)(kh−1)/(k−1) 个节点,最少 k+1+h-2k+1+h−2 个结点(h\geq 2h≥2)。
(8)具有 nn 个结点的 kk 叉树的最小高度为 \lceil \log_k{n(k-1)+1}\rceil⌈logkn(k−1)+1⌉。
因此,我们可以利用树的基本性质来判断某问题的数据结构是不是树结构。
你可以证明上面的各种性质吗?
四、课堂练习&课后作业
举出生活中的一些有根树的例子,并尝试画出来,越多越好;
举出生活中的一些无根树的例子,并尝试画出来,越多越好;
按照要求,找出下图中树所包含的信息。

(1)求出树的结点数、边数、度和高度;
(2)求出每个结点的深度,以及每个结点的父节点和孩子结点;
(3)找出上树中所有的兄弟、堂兄弟、祖先关系;
(4)找出每个结点的子树数量,并画出对应的子树。
编程题(P2806 儿子数量 I - TopsCoding)
问题描述:求树中每个点的儿子数,假设结点 1 为树的根。
输入格式:第一行一个整数 nn,表示树的结点个数。后面有 n-1n−1 行,每行两个整数 x,yx,y,表示 xx 是 yy 的父结点。
输出格式:nn 个整数,第 ii 个整数位结点 ii 的儿子个数。输入样例:
7 1 2 1 3 1 5 2 4 2 6 3 7Copy
输出样例:
3 2 1 0 0 0 0Copy
编程题(P2807 儿子数量 II - TopsCoding)
问题描述:求树中每个点的儿子数,假设结点 1 为树的根。
输入格式:第一行一个整数 nn,表示树的结点个数。后面有 n-1n−1 行,每行两个整数 x,yx,y,但不保证 xx 是 yy 的父亲。
输出格式:nn 个整数,第 ii 个整数位结点 ii 的儿子个数。输入样例:
7 2 1 1 3 5 1 4 2 2 6 7 3Copy
输出样例:
3 2 1 0 0 0 0Copy
边栏推荐
- 队列与栈
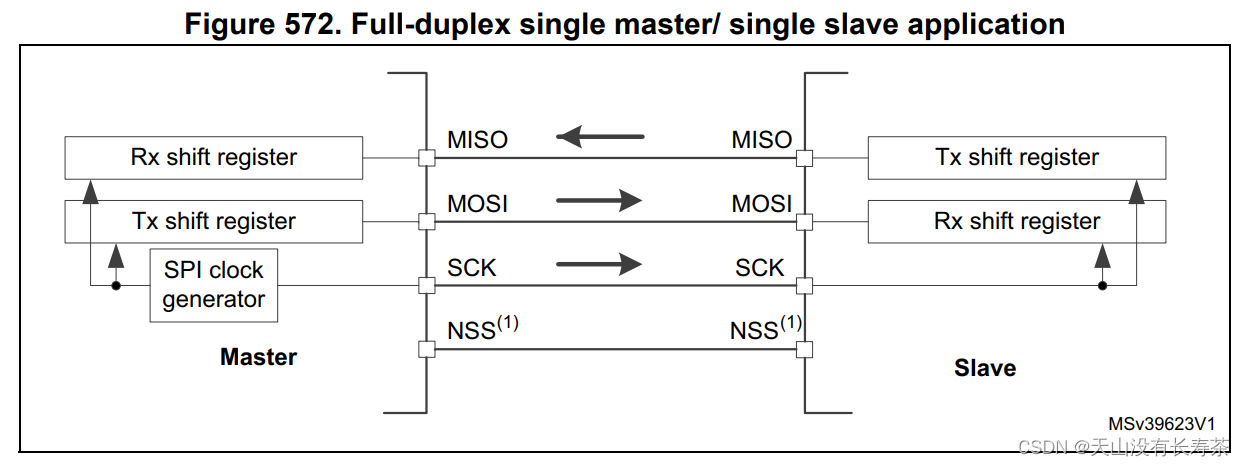
- STM32LL library use - SPI communication
- Mysql连接错误解决
- Open the door to electricity "Circuit" (3): Talk about different resistance and conductance
- Summarize computer network super comprehensive test questions
- Mysql lock
- Win10上帝模式干嘛的?Win10怎么开启上帝模式?
- Redis的线程模型
- 5. Transaction management
- 一篇文章彻底理解Redis的持久化:RDB、AOF
猜你喜欢
随机推荐
cmake configure libtorch error Failed to compute shorthash for libnvrtc.so
Introduction to in-order traversal (non-recursive, recursive) after binary tree traversal
专硕与学硕
win10 system update error code 0x80244022 how to do
二叉排序树与 set、map
Win10电脑需要安装杀毒软件吗?
Codeforces Round #605 (Div. 3)
MATLAB drawing command fimplicit detailed introduction to drawing implicit function graphics
总结计算机网络超全面试题
为vscode配置clangd
win11一直弹出用户账户控制怎么解决
Redis常见面试题
Actual combat Meituan Nuxt +Vue family bucket, server-side rendering, mailbox verification, passport authentication service, map API reference, mongodb, redis and other technical points
What should I do if the Win10 system sets the application identity to automatically prompt for access denied?
基于矩阵计算的线性回归分析方程中系数的估计
Article pygame drag the implementation of the method
Daily - Notes
使用libcurl将Opencv Mat的图像上传到文件服务器,基于post请求和ftp协议两种方法
Win11没有本地用户和组怎么解决
How to update Win11 sound card driver?Win11 sound card driver update method