当前位置:网站首页>775 Div.1 C. Tyler and strings combinatorial mathematics
775 Div.1 C. Tyler and strings combinatorial mathematics
2022-07-05 04:45:00 【Strezia】
C
Combinatorial mathematics ,1900, Array of numbers
The question
give s , t s, t s,t Two sequences , The lengths are n , m n,m n,m, ask s s s How many sorting methods meet s s s The dictionary order of t t t Small . 1 ≤ n , m ≤ 2 e 5 1\leq n,m\leq 2e5 1≤n,m≤2e5
Ideas
Because it is compared in dictionary order , So if s 1 < t 1 s_1<t_1 s1<t1 After that, you can row at will , So before considering enumeration i − 1 i-1 i−1 The bits are the same and s i < t i s_i<t_i si<ti The sorting methods of are c n t i cnt_i cnti Kind of , The final answer is ∑ i = 1 i = n c n t i \sum_{i=1}^{i=n} cnt_i ∑i=1i=ncnti .
So how to ask c n t i cnt_i cnti Well ? If repeatable arrangement is not considered , that c n t i = n o w × ( n − i ) ! cnt_i= now \times (n-i)! cnti=now×(n−i)! , namely To the first i Bit current Satisfaction is less than t i t_i ti Multiply the number of by the total arrangement of the following numbers ( because i i i The following numbers can be taken at will ). n o w now now You can directly use the number array to maintain the prefix and ( Because of the former i − 1 i-1 i−1 The two bit sequences are the same , So you can directly reduce that number 1). So the key problem is how to add repeatable permutation .
First, the repeatable arrangement should be in n ! n! n! Divided by the factorial of the number of occurrences of each element . That is, when we traverse to i i i When a , To be in ( n − i ) ! (n-i)! (n−i)! Divided by c n t 1 ! × c n t 2 ! × c n t i ! . . . . × c n t n ! {cnt_1!\times cnt_2!\times cnt_i!....\times cnt_n!} cnt1!×cnt2!×cnti!....×cntn!
among c n t 1 cnt_1 cnt1 yes Before subtraction i − 1 i-1 i−1 Digit number The number of corresponding numbers after . Then we can preprocess out i = 0 i=0 i=0 The above formula of tense is recorded as fenzi, from
1 c n t 1 ! × c n t 2 ! × ( c n t i − 1 ) ! . . . . × c n t n ! = 1 c n t 1 ! × c n t 2 ! × c n t i ! . . . . × c n t n ! × c n t i \frac{1}{cnt_1!\times cnt_2!\times (cnt_i-1)!....\times cnt_n!}=\frac{1}{cnt_1!\times cnt_2!\times cnt_i!....\times cnt_n!}\times cnt_i cnt1!×cnt2!×(cnti−1)!....×cntn!1=cnt1!×cnt2!×cnti!....×cntn!1×cnti, After each iteration, you just need to fenzi *= cnt[t[i]] And update the cnt[t[i]] that will do .
ps. Don't forget to consider s s s It may happen to be t t t Prefix of , Began to forget , Fortunately, there are examples 1
Code
void solve() {
cin >> n >> m;
fac[0] = 1;
for(int i = 1; i <= n; i++) {
fac[i] = (fac[i-1] * i) % P;
}
for(int i = 1; i <= n; i++) {
cin >> s[i];
update(s[i], 1);
cnt[s[i]]++;
}
for(int i = 1; i <= m; i++) {
cin >> t[i];
}
int ans = 0;
int mi = min(n, m);
int fz = 1;
for(int i = 1; i <= 2e5; i++) {
if(cnt[i]) {
fz = fz * fac[cnt[i]] % P;
}
}
fz = power(fz, P - 2);
int flag = 1;
if(n >= m) {
flag = 0;
}
for(int i = 1; i <= mi; i++) {
int p = ask(t[i] - 1);
ans = (ans + p * fac[n-i] % P * fz % P) % P;
if(!cnt[t[i]]) {
flag = 0;
break;
}
fz = fz * cnt[t[i]] % P;
cnt[t[i]]--;
update(t[i], -1);
}
ans += flag;
ans %= P;
cout << ans << endl;
}
边栏推荐
- [ideas] 2021 may day mathematical modeling competition / May Day mathematical modeling ideas + references + codes
- level18
- Reading and visualization of DICOM, MHD and raw files in medical imaging
- PHP reads the INI file and writes the modified content
- 概率论与数理统计考试重点复习路线
- 直播預告 | 容器服務 ACK 彈性預測最佳實踐
- [groovy] closure (Introduction to closure class closure | closure parametertypes and maximumnumberofparameters member usage)
- How should programmers learn mathematics
- Moco is not suitable for target detection? MsrA proposes object level comparative learning target detection pre training method SOCO! Performance SOTA! (NeurIPS 2021)...
- Hypothesis testing -- learning notes of Chapter 8 of probability theory and mathematical statistics
猜你喜欢
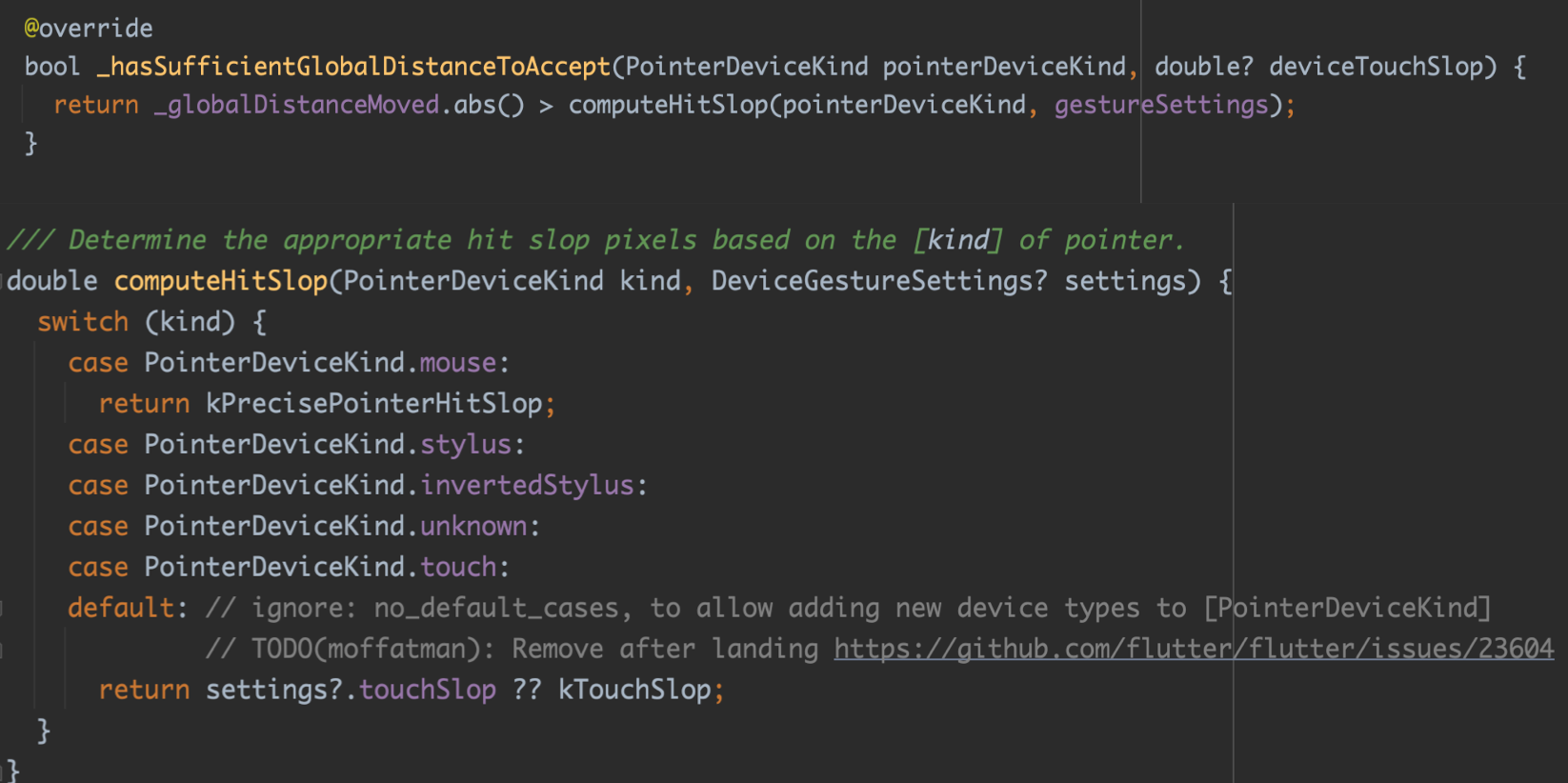
Flutter 小技巧之 ListView 和 PageView 的各种花式嵌套
![[groovy] closure closure (customize closure parameters | customize a single closure parameter | customize multiple closure parameters | specify the default value of closure parameters)](/img/92/937122b059b6f3a91ae0e0858685e7.jpg)
[groovy] closure closure (customize closure parameters | customize a single closure parameter | customize multiple closure parameters | specify the default value of closure parameters)

JVM 原理和流程简介
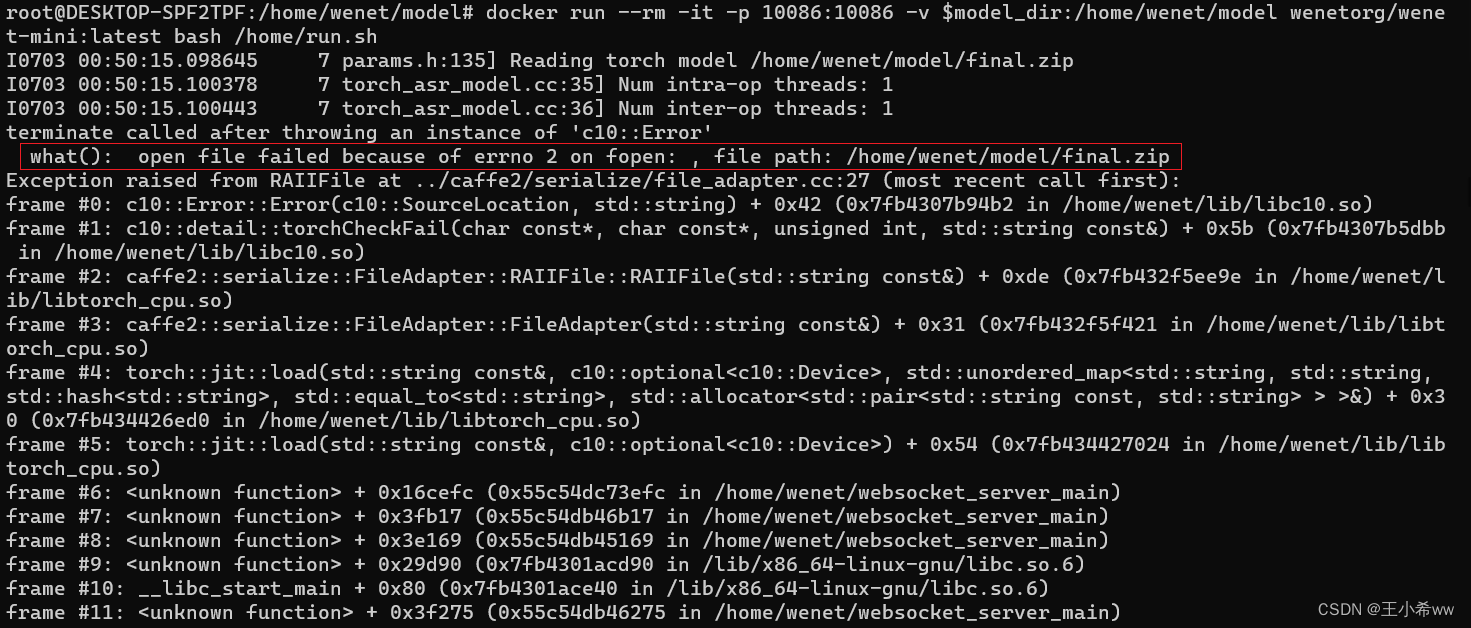
Wenet: E2E speech recognition tool for industrial implementation
![[PCL self study: feature9] global aligned spatial distribution (GASD) descriptor (continuously updated)](/img/2b/933586b6feff1d48c5bee11cd734ba.jpg)
[PCL self study: feature9] global aligned spatial distribution (GASD) descriptor (continuously updated)
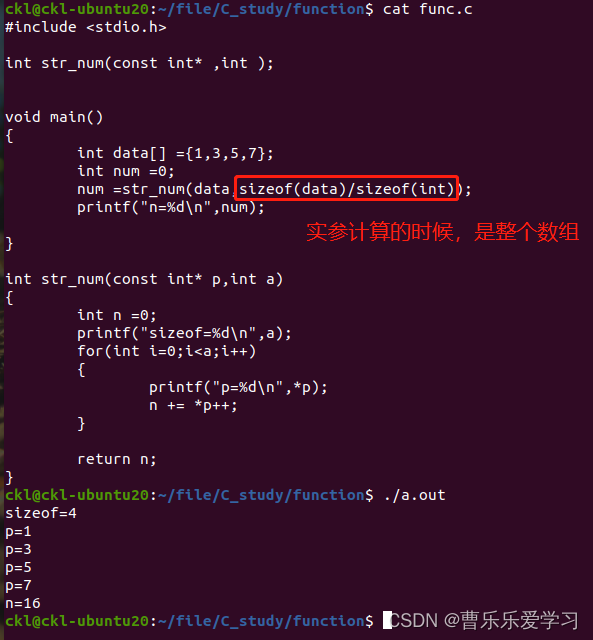
函數(易錯)
![[groovy] closure (closure call is associated with call method | call () method is defined in interface | call () method is defined in class | code example)](/img/03/329adb314606f29c8a4cb2260e84c8.jpg)
[groovy] closure (closure call is associated with call method | call () method is defined in interface | call () method is defined in class | code example)

CUDA Programming atomic operation atomicadd reports error err:msb3721, return code 1

函数(易错)
![[groovy] closure (closure parameter list rule | default parameter list | do not receive parameters | receive custom parameters)](/img/36/c4206a95c007e41df628d99e06ba18.jpg)
[groovy] closure (closure parameter list rule | default parameter list | do not receive parameters | receive custom parameters)
随机推荐
函数(基本:参数,返回值)
2022 thinking of mathematical modeling a problem of American college students / analysis of 2022 American competition a problem
Decimal to hexadecimal
Group counting notes (1) - check code, original complement multiplication and division calculation, floating point calculation
如何进行「小步重构」?
Is $20billion a little less? Cisco is interested in Splunk?
Discussion on the dimension of confrontation subspace
【科普】热设计基础知识:5G光器件之散热分析
What are the building energy-saving software
Moco is not suitable for target detection? MsrA proposes object level comparative learning target detection pre training method SOCO! Performance SOTA! (NeurIPS 2021)...
[popular science] basic knowledge of thermal design: heat dissipation analysis of 5g optical devices
【acwing】240. food chain
49 pictures and 26 questions explain in detail what is WiFi?
[Chongqing Guangdong education] National Open University 2047t commercial bank operation and management reference test in autumn 2018
Aperçu en direct | Services de conteneurs ACK flexible Prediction Best Practices
OWASP top 10 vulnerability Guide (2021)
函數(易錯)
[crampon programming] lintcode decoding Encyclopedia - 1100 strange printer
托管式服务网络:云原生时代的应用体系架构进化
【acwing】836. Merge sets