Solution to game 10 of the personal field

Flowers shuffle

Title Description
There are many ways to shuffle . Japanese card games “hanafuda” The shuffle of is an example . Here is how to execute Hanafuda Shuffle .

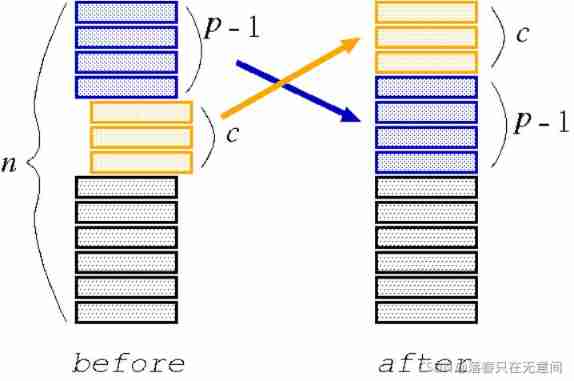
There is a pair n card . From the top of the deck p This card starts ,c The card is pulled out and placed on top of the card set , Pictured 1 Shown . This operation is called cutting operation , Then repeat .

Write a program , Simulate Playboy shuffle , And answer which card will eventually be placed at the top of the deck .

Input format
The input contains multiple sets of data .

For each group of data, first enter a row of two integers separated by spaces n and r, They are the number of cards in the group and the number of clipping operations 1≤n≤50,1≤r≤50.
Next input r That's ok , Each row represents a cutting operation . These cutting operations are performed in the order listed . Each line contains two positive integers p and c（p+c<=n+1）. From the top of the deck p This card starts ,c The card should be drawn out and placed on the top .

Enter two separated by spaces 0 ending

Output format
For each set of data , Output the number of the last card on the top of the stack , Cards are initially numbered from bottom to top 1-n

The main idea of the topic ：

There is a pile of cards , Number from 1...n, From p Cards begin to be taken out backwards c Put a card at the bottom . The top here is number n Behind . At the same time, pay attention to when putting the card on the top , From the front card to the back .

Their thinking ：

We use arrays to simulate this process , We save after going n~1, At this time, the subscript is 1 The top is where the . At the same time, an additional array is used to store the data after the operation . The process of simulation is to c Put a card in front c A place , Then fill in the following data .

Code ：

#include <stdio.h>
#include <cstring>

int game[100];
int n, r;

int main() {
    
	while (~scanf("%d%d", &n, &r)) {
    
		if (!n && !r)
			break;
		for (int i = 0; i <= n; ++i)
			game[i] = n - i + 1;
		int barcup[200];
		memcpy(barcup, game, sizeof game);
		//  With  10 9 8 7 6 5 4 3 2 1  For example 
		while (r--) {
    
			int p, c;
			scanf("%d%d", &p, &c);
			// p = 8,c = 3;
			//  Will be the first 8 A start 3 Put it on the top , namely  4,3,2
			for (int i = p + c - 1, j = c; i >= p; --i, --j)
				barcup[j] = game[i];
			// 4 3 2 7 6 5 4 3 2 1
			//  After the   The first 1 Position to the first  p-1  Put the element for behind 
			for (int i = c + 1, j = 1; j <=  p - 1; i++, ++j)
				barcup[i] = game[j];
			// 4 3 2 10 9 8 7 6 5 1
			memcpy(game, barcup, sizeof game);
		}
		printf("%d\n", game[1]);

	}
	return 0;
}

Point and circle

Known in Cartesian coordinates N A little bit . You have a radius of 1 The circle of , And move it in Cartesian coordinates , So as to surround these points as much as possible . Find out how many points can be surrounded at the same time . When the point is in or on a circle , It is thought to be surrounded by circles .

Input
The input consists of a series of data sets , Followed by a line , Contains only one character ’0’, This indicates the end of the input . Each data set contains integers N Start of line for ,N Indicates the number of points in the data set . Back N The line describes the coordinates of the point . Each line has two decimals X and Y, Describe the points respectively X and Y coordinate . Keep five digits after the decimal point .

You can assume 1 <= N <= 300, 0.0 <= X <= 10.0, 0.0 <= Y <= 10.0. No distance between two points is less than 0.0001. The distance between no two points in the dataset is approximately 2.0. More precisely , For any two points in the data set , The distance between the two d Never satisfied 1.9999 <= d <= 2.0001. Last , No three points in a dataset are very close to a radius of 1 The circle of . More precisely , Give Way P1, P2, P3 Is any three points in the data set ,d1, d2, d3 Are the distances from any point in the Cartesian coordinate system to these three points . Then it will never hold at the same time 0.9999 <= di <= 1.0001 (i = 1,2,3).

Output
For each data set , Print a single line , The included data set can be divided into 1 The maximum number of points surrounded by a circle . No other characters should be printed , Including leading and trailing spaces .

The solution is , Turn the question into a specific form of answer . Draw a picture. Let's assume that there is a circle containing a push point inside , We move the circle when we can always include all points , First of all, the circle intersects with one of the points , At this time, I am satisfied , When it intersects two points , If you also move the circle, it cannot contain all the points . So the limit is two points .
So we can enumerate the combination of two different points , Calculate the center of the circle passing through these two points , Then because it's unit yuan , Traverse all points if the distance from the center of the circle is within the circle +1, Take the maximum value of this result .

matters needing attention ：

• One point , So we initialize to 1 that will do .
• Because if the distance between two points is greater than 2 It doesn't count .

Code ：

#include <stdio.h>
#include <math.h>
#include <algorithm>

using namespace std;
const double eps = 1e-8;
struct point {
    
	double x, y;
} p[3010];
int n;


double dist(point a, point b) {
    
	return sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));
}

//  Two points on the circle are known , Find the coordinates of the center of the circle 
void getmid(point p1, point p2, point &center) {
    
	point mid;
	mid.x = (p1.x + p2.x) / 2.0;
	mid.y = (p1.y + p2.y) / 2.0;
	double angle = atan2(p1.x - p2.x, p2.y - p1.y);
	double dcm = sqrt(1 - dist(p1, mid) * dist(p1, mid));
	center.x = mid.x + dcm * cos(angle);
	center.y = mid.y + dcm * sin(angle);
}

int main() {
    
	while (~scanf("%d", &n)) {
    
		if (!n)
			break;
		for (int i = 1; i <= n; ++i)
			scanf("%lf%lf", &p[i].x, &p[i].y);
		int ans = 1, cnt = 0;
		for (int i = 1; i < n; ++i)
			for (int j = i + 1; j <= n; ++j) {
    
				if (dist(p[i], p[j]) > 2.0)
					continue;
				point center;
				getmid(p[i], p[j], center);
				int cnt = 0;
				for (int k = 1; k <= n; ++k) {
    
					if (dist(p[k], center) < 1.0 + eps)
						cnt++;
				}
				ans = max(ans, cnt);
			}
		printf("%d\n", ans);
	}
	return 0;
}

Division of unit scores

Input format
The molecule is 1, Fractions whose denominator is a positive integer are called unit fractions . Positive rational numbers p/q The expression of the sum of the fractions of a finite number of units is called p/q To the division of unit scores . for example ,1/2+1/6 Yes, it will 2/3 A way of dividing into unit fractions . The difference in the order of addition is ignored . for example , We don't distinguish 1/6+1/2 and 1/2+1/6.

For a given four positive integers p、q、a and n, take p/q The number of partitions of is calculated as the unit fraction meeting the following two conditions .

Divided into the most n Sum of unit scores .

The product of denominator of unit fraction in division is less than or equal to a
for example , If (p,q,a,n)=(2,3,120,3), We can find the following four divisions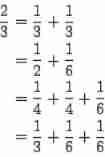

Input format
Input no more than 1000 Group data

For each set of data , Input p q a n, Two adjacent numbers are separated by spaces ,p,q≤800,a≤12000,n≤7

Enter to contain four spaces separated 0 end

Output format
For each set of data , Output an integer , Indicates the number of partition schemes

The question ：

Gave a score p/q, Find out how many kinds of units the sum of fractions is equal to p/q, And the product of denominators of all unit fractions is less than or equal to a, The number is less than n.

Ideas ：

Denominator from 1 Start enumeration , Record the enumeration number every time , If the denominator is satisfied ji The product is less than or equal to a, And the number does not exceed n, Let's continue searching from this number , Because there is no order between unit scores , So this covers all situations .

Code ：

#include <stdio.h>
#include <cstring>

int p, q, a, n;
int ans;
void dfs(int p, int q, int mul, int x, int num) {
    
	if (p == 0 && mul <= a) {
    
		ans ++;
		return ;
	}
	//  prune 
	//  Respectively   The quantity reaches the upper limit ,mul * x  It is the smallest denominator to multiply later 
	// The value of this is greater than  a  There is no need to play .
	// p*x>q*num  That is, because this path multiplies the denominator back >= x
	if (num == 0 || mul * x > a || p * x > q * num)
		return ;
	for (int i = x; i <= a ; ++i) {
    
		if (mul * i <= a) {
    
			int dp = p * i - q; //  Can't change directly p Ah, otherwise, this once was not based on p For the root 
			if (p >= 0)
				dfs(dp, q * i, mul * i, i, num - 1);
		}
	}
}


int main() {
    
	while (~scanf("%d%d%d%d", &p, &q, &a, &n)) {
    
		if (!p && !q && !n && !a)
			break;
		ans = 0;
		dfs(p, q, 1, 1, n);
		printf("%d\n", ans);
	}
	return 0;
}