Several classes and functions that must be clarified when using Ceres to slam

Ceres solver It is a product developed by Google for Nonlinear optimization The library of , Open source lidar at Google slam project cartographer Is widely used .
It was said in the previous blog , The essence of graph optimization is a nonlinear optimization problem . therefore ceres Just right for Graph optimization Problem solving .
It can also be used to iteratively optimize the optimal transposition posture after feature point matching ceres.

ceres brief introduction

Ceres It can solve the boundary constrained robust nonlinear least square optimization problem . This concept can be expressed by the following expression ：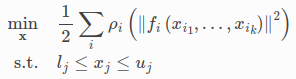

This expression is widely used in engineering and Science . For example, curve fitting in Statistics , Or build a three-dimensional model based on images in computer vision .

Be careful There are several special concepts to be familiar with in each module of this formula , It involves specific use :

Residual block （ResidualBlock）: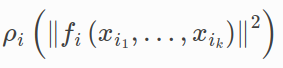

This part is called the residual block （ResidualBlock）.

Cost function （CostFunction）:

This part is called the cost function （CostFunction）.

Parameter block （ParameterBlock）:

The cost function depends on a series of parameters , This series of parameters （ They are scalars ） It is called parameter block （ParameterBlock）. Of course, the parameter block can also contain only one variable

Up and down the border :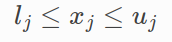

lj and uj yes xj The upper and lower boundaries of .

Loss function （LossFunction）: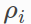

pi Is the loss function （LossFunction）. According to the loss function is a scalar function , Its function is to reduce outliers （Outliers） Impact on optimization results . The effect is similar to filtering functions .

ceres Use process of

1. Build cost function (cost function)
2. The optimization problem to be solved is constructed by cost function
3. Configure solver parameters and solve the problem

ceres Classes and functions that must be known

class LossFunction

class LossFunction Loss function
The input data of the least squares problem may contain outliers ( Measured incorrectly ), Use the loss function to reduce the impact of this part of the data .

For example, in a scene with a mobile camera , There are fire hydrants and cars on the street , When the image processing algorithm matches the tip of the fire hydrant with the headlights of the car , Then if nothing is done , Will lead to ceres In order to reduce the large error of this error , But the optimization result deviates from the correct position .

LossFunction It can reduce the weight of large residuals , Thus to The final optimization result has little impact .

class LossFunction {
    
 public:
  virtual void Evaluate(double s, double out[3]) const = 0;
};

LossFunction Class , The key function is LossFunction::Evaluate()
A nonnegative parameter s, Calculate the output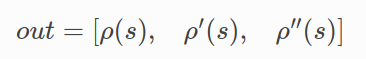

Ceres It includes several defined loss functions , There is no scaling . The specific effect is shown in the figure below :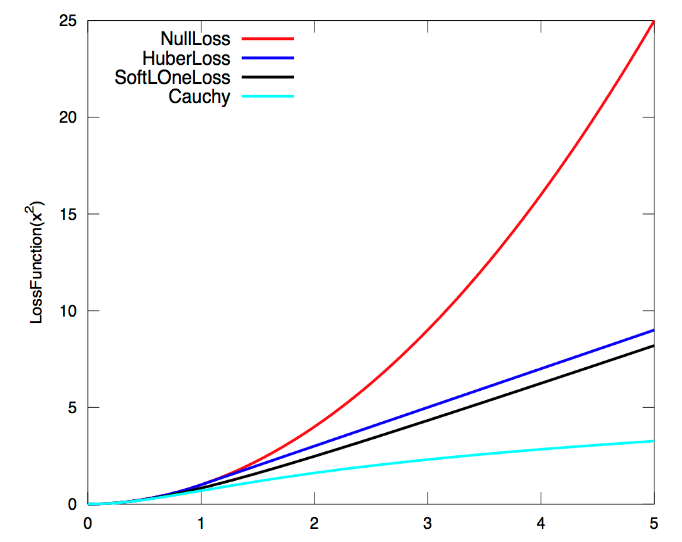

The red one in the figure is the one without loss function ,y=x*x. The blue one is HuberLoss, Value below normal , also x The bigger it is , The more obvious the effect .
Normal is :

HuberLoss yes :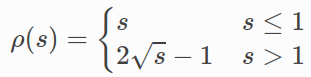

SoftLOneLoss yes :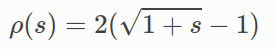

CauchyLoss yes :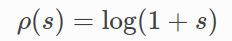

ArctanLoss yes :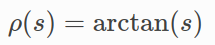

TolerantLoss yes :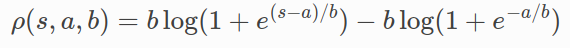

Using the defined loss function is also very simple . for example :

ceres::LossFunction *loss_function = new ceres::HuberLoss(0.1);

Definition ceres Of Loss function 0.1 representative The residual is greater than 0.1 The point of , Then the weight decreases , See the above formula for the specific effect . Less than 0.1 Is considered normal , No special treatment
After definition , Adding residuals

LocalParameterization

LocalParameterization Local parameters
In many optimization problems , Especially in the problem of sensor fusion , The quantities that exist in a space called a manifold must be modeled , For example, the rotation of the sensor is represented by the number of quaternions / Direction .

Ceres Some special parameters are defined , about slam, What we use more is the quaternion of rotation
QuaternionParameterization
EigenQuaternionParameterization
There are two main reasons for defining Eigen The way of storing quaternions is different from general ,Eigen yes x,y,z,w, Real part w In the last , Generally speaking :w,x,y,z.

Use

double para_q[4] = {
    0, 0, 0, 1};
ceres::LocalParameterization *q_parameterization =
new ceres::EigenQuaternionParameterization();
problem.AddParameterBlock(para_q, 4, q_parameterization);

class problem

problem Class is the least square problem with bilateral constraints
To create a least squares problem , Need to use
Problem::AddResidalBlock() Add residual module
Problem::AddParameterBlock() Add parameter module
These two methods

for instance , A problem contains three parameter modules , The dimensions are 3,4,5, The sizes of the two residual modules are 2 and 6

double x1[] = {
     1.0, 2.0, 3.0 };
double x2[] = {
     1.0, 2.0, 3.0, 5.0 };
double x3[] = {
     1.0, 2.0, 3.0, 6.0, 7.0 };

Problem problem;
problem.AddResidualBlock(new MyUnaryCostFunction(...), x1);
problem.AddResidualBlock(new MyBinaryCostFunction(...), x2, x3);

Method Problem::AddResidualBlock(), It's the same as the name , The function is to add parameter modules to problem in , This method must have parameters CostFunction And optional parameters LossFunction, This method connects CostFunction and Parameter module .
CostFunction Information with its desired parameter block size .
This function checks whether these are related to parameter_blocks Match the size of the parameter block listed in . If an incorrect match is detected , The program will terminate .
LossFunction There can be , There can be no

have access to Problem::AddParameterBlock() This method is used to add parameter modules , This will add a parameter size detection . Add parameter blocks explicitly to the problem . It is also allowed to Manifold Objects are associated with parameter blocks .
This function can be used with LocalParameterization Parameters of , It's also possible to do without .

problem.AddParameterBlock(para_q, 4, q_parameterization);//  Add a quaternion parameter block 
problem.AddParameterBlock(para_t, 3);// Add the parameter block of Translation 

This is generally the case when declaring :

ceres::Problem::Options problem_options;
ceres::Problem problem(problem_options);

Let me declare one ceres::Problem::Options, And then use Options initialization problem

class CostFunction

Cost function CostFunction Responsible for calculating residual vector and Jacobian matrix .
Cost function dependent parameter block

Its internal definition is like this

class CostFunction {
    
 public:
  virtual bool Evaluate(double const* const* parameters,
                        double* residuals,
                        double** jacobians) = 0;
  const vector<int32>& parameter_block_sizes();
  int num_residuals() const;

 protected:
  vector<int32>* mutable_parameter_block_sizes();
  void set_num_residuals(int num_residuals);
};

Don't worry about this part , Because when used, the interior of this class defined by other classes
Definition CostFunction or SizedCostFunction May be error prone , Especially when calculating derivatives . So ,Ceres Automatic differentiation is provided .

class AutoDiffCostFunction

Definition CostFunction or SizedCostFunction May be error prone , Especially when calculating derivatives . So ,Ceres Automatic differentiation is provided .

template <typename CostFunctor,
       int kNumResiduals,  // Number of residuals, or ceres::DYNAMIC.
       int... Ns>          // Size of each parameter block
class AutoDiffCostFunction : public SizedCostFunction<kNumResiduals, Ns> {
    
 public:
  AutoDiffCostFunction(CostFunctor* functor, ownership = TAKE_OWNERSHIP);
  // Ignore the template parameter kNumResiduals and use
  // num_residuals instead.
  AutoDiffCostFunction(CostFunctor* functor,
                       int num_residuals,
                       ownership = TAKE_OWNERSHIP);
};

Get a cost function that can automatically derive , You must define a class or structure to overload operators , In it, we can calculate the cost function with parameter template , The overloaded operator must store the calculation result in the last parameter , And back to true.

for instance , To calculate One The cost function is e= k - xTy.
x and y It's a two-dimensional vector ,k Is a constant parameter .
Then you can define such a class

class MyScalarCostFunctor {
    
  MyScalarCostFunctor(double k): k_(k) {
    }

  template <typename T>
  bool operator()(const T* const x , const T* const y, T* e) const {
    
    e[0] = k_ - x[0] * y[0] - x[1] * y[1];
    return true;
  }

 private:
  double k_;
};

In the definition of overloaded operators . Parameters x and y in front , If there are more input parameters , Then you can continue to line up y Back , The output, that is, the residual, is placed in the last parameter ,

Given the definition of this class , Its automatic differential cost function can be defined as follows :

CostFunction* cost_function
    = new AutoDiffCostFunction<MyScalarCostFunctor, 1, 2, 2>(
        new MyScalarCostFunctor(1.0));              ^  ^  ^
                                                    |  |  |
                        Dimension of residual ------+  |  |
                        Dimension of x ----------------+  |
                        Dimension of y -------------------+

above 1,2,2 That's what the notes say , Calculation 1 Residual of dimension ,2 individual 2 Optimization quantity of dimension