当前位置:网站首页>HDU 4661 message passing (wood DP & amp; Combinatorics)
HDU 4661 message passing (wood DP & amp; Combinatorics)
2022-07-07 01:42:00 【Full stack programmer webmaster】
Hello everyone , I meet you again , I'm the king of the whole stack
Message Passing
Time Limit: 10000/5000 MS (Java/Others) Memory Limit: 131072/131072 K (Java/Others) Total Submission(s): 1187 Accepted Submission(s): 423
Problem Description
There are n people numbered from 1 to n. Each people have a unique message. Some pairs of people can send messages directly to each other, and this relationship forms a structure of a tree. In one turn, exactly one person sends all messages s/he currently has to another person. What is the minimum number of turns needed so that everyone has all the messages? This is not your task. Your task is: count the number of ways that minimizes the number of turns. Two ways are different if there exists some k such that in the k-th turn, the sender or receiver is different in the two ways.
Input
First line, number of test cases, T. Following are T test cases. For each test case, the first line is number of people, n. Following are n-1 lines. Each line contains two numbers.
Sum of all n <= 1000000.
Output
T lines, each line is answer to the corresponding test case. Since the answers may be very large, you should output them modulo 10 9+7.
Sample Input
2
2
1 2
3
1 2
2 3Sample Output
2
6Source
zhuyuanchen520 | We have carefully selected several similar problems for you: 501750155013
The question :
n personal , Form a tree relationship . Everyone has a unique message . Everyone can pass their information through the tree . Share with his neighbors , After sharing . The person who is shared has his original information and shared information .
Each share is an operation . Ask how many sharing methods are there for each person to have all their information for the minimum number of times .
Ideas :
easy Out of . In the shortest time . Of course, each node wants to send its own information out once . And receive a message , That is, by the tree 2 times 2*(n-1). Then we can prove . In the shortest time , All delivery methods have one “ Information conversion point ”—— The information of other nodes is first transferred to this node , Then the information is transferred from this node to other nodes .
In fact, what we need is how many kinds of topological orders . Definition dp[u] Express u Below the node . to u How many kinds of topological orders of nodes ,cnt[u] Express u How many children and grandchildren are there ,f[i] = i!(i The factorial ).c[i][j] Represents the number of combinations .
If it has v1,v2,v3 Nodes . Their topological orders are dp[v1],dp[v2],dp[v3] So many .
that dp[u] = c[cnt[u]-1][cnt[v1]] * c[cnt[u]-1-cnt[v1]][cnt[v2]] * c[cnt[u]-1-cnt[v1]-cnt[v2]][cnt[v3]] * dp[v1] * dp[v2] * dp[v3]( Push this by yourself ). After simplification . obtain dp[u] = f[cnt[u]-1] / ( f[cnt[v1]] * f[cnt[v2]] * f[cnt[v3]] ) * dp[v1] * dp[v2] * dp[v3] . We can o(n) The time complexity is calculated with 1 All nodes with root dp value ( So in order to 1 The answer for root is calculated ). And some other auxiliary information . Then traverse down according to the tree structure . Calculate the answers rooted in other nodes respectively . The above is the online thinking . What I want to say is my understanding . Why do you know the number of topological orders of each subtree . You can exit your topological order number . In fact, it's very easy to understand . When the topological order of each subtree is determined . When determining the overall order .
That is to get a length of cnt[u] The topological sequence .
For subtrees i.
There is also a length of cnt[i] The topological sequence , So it's about cnt[u] Look inside cnt[i] A place . Look for other subtrees in the remaining subtrees .
And how to deduce when changing the root . Write first
dp[u]’=dp[u]*(n-sz[v]-1)!*sz[v]!/((n-1)!*dp[v])
dp[v]’=dp[v]*(n-1)!*dp[u]’/((sz[v]-1)!*(n-sz[v])!).
Into the dp[u]’ You can ask for a lot of things . So don't rush to get the final answer when pushing the formula . There is also why the answer number is the square of the topological ordinal .
Because when the information is sent back, it is your topological order . Same as topological ordinal .
Each positive topological order can be combined with an inverse topological order . So there are square species .
See code for details :
#include<algorithm>
#include<iostream>
#include<string.h>
#include<stdio.h>
using namespace std;
const int INF=0x3f3f3f3f;
const int maxn=1000010;
#pragma comment(linker, "/STACK:1024000000,1024000000")
typedef long long ll;
const ll mod=1e9+7;
ll fac[maxn],dp[maxn],ans;
int cnt,sz[maxn],n;
struct node
{
int v;
node *next;
} ed[maxn<<1],*head[maxn];
void adde(int u,int v)
{
ed[cnt].v=v;
ed[cnt].next=head[u];
head[u]=&ed[cnt++];
}
ll pow_mod(ll x,int k)
{
ll base=x,ret=1;
while(k)
{
if(k&1)
ret=(ret*base)%mod;
base=(base*base)%mod;
k>>=1;
}
return ret;
}
ll ni(ll x){ return pow_mod(x,mod-2); }
void dfs(int fa,int u)
{
ll tp;
dp[u]=tp=sz[u]=1;
for(node *p=head[u];p!=NULL;p=p->next)
{
int v=p->v;
if(v==fa)
continue;
dfs(u,v);
tp=(tp*ni(fac[sz[v]]))%mod;
dp[u]=(dp[u]*dp[v])%mod;
sz[u]+=sz[v];
}
dp[u]=(dp[u]*fac[sz[u]-1]%mod*tp)%mod;
}
void solve(int fa,int u,ll tp)
{
ll tt;
ans=(ans+tp*tp%mod)%mod;
for(node *p=head[u];p!=NULL;p=p->next)
{
int v=p->v;
if(v==fa)
continue;
tt=(tp*fac[n-sz[v]-1]%mod*fac[sz[v]])%mod;
tt=(tt*ni(fac[sz[v]-1])%mod*ni(fac[n-sz[v]]))%mod;
solve(u,v,tt);
}
}
int main()
{
int t,i,u,v,rt;
fac[0]=fac[1]=1;
for(i=2;i<maxn;i++)
fac[i]=(i*fac[i-1])%mod;
scanf("%d",&t);
while(t--)
{
scanf("%d",&n);
cnt=0,ans=0;
for(i=1;i<=n;i++)
head[i]=NULL;
for(i=1;i<n;i++)
{
scanf("%d%d",&u,&v);
adde(u,v);
adde(v,u);
}
rt=(n+1)/2;
dfs(-1,rt);
solve(-1,rt,dp[rt]);
printf("%I64d\n",ans);
}
return 0;
}Copyright notice : This article is the original article of the blogger , Blog , Do not reprint without permission .
Publisher : Full stack programmer stack length , Reprint please indicate the source :https://javaforall.cn/116894.html Link to the original text :https://javaforall.cn
边栏推荐
- AcWing 344. Solution to the problem of sightseeing tour (Floyd finding the minimum ring of undirected graph)
- Drag to change order
- 各种语言,软件,系统的国内镜像,收藏这一个仓库就够了: Thanks-Mirror
- swiper组件中使用video导致全屏错位
- LeetCode:1175. Prime permutation
- 长按按钮执行函数
- What does front-end processor mean? What is the main function? What is the difference with fortress machine?
- 爬虫实战(六):爬笔趣阁小说
- 字符串的相关编程题
- IDEA常用的快捷键
猜你喜欢

454 Baidu Mianjing 1
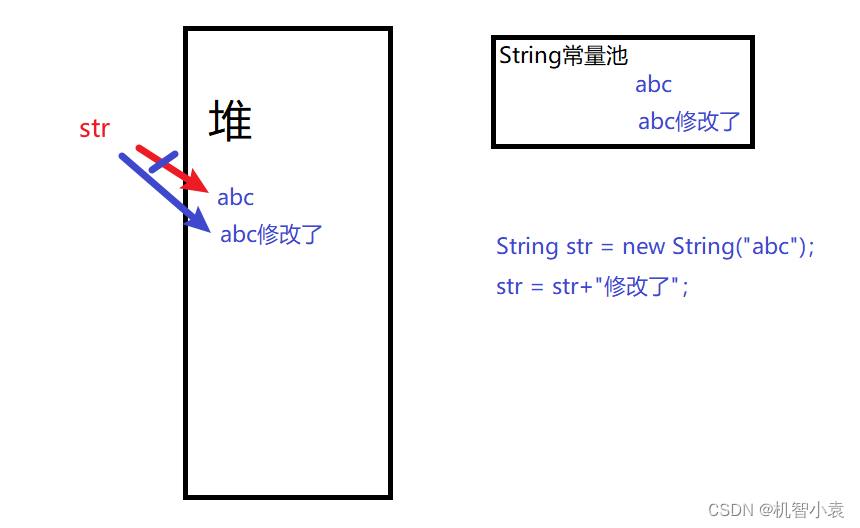
今日问题-2022/7/4 lambda体中修改String引用类型变量

How to manage distributed teams?
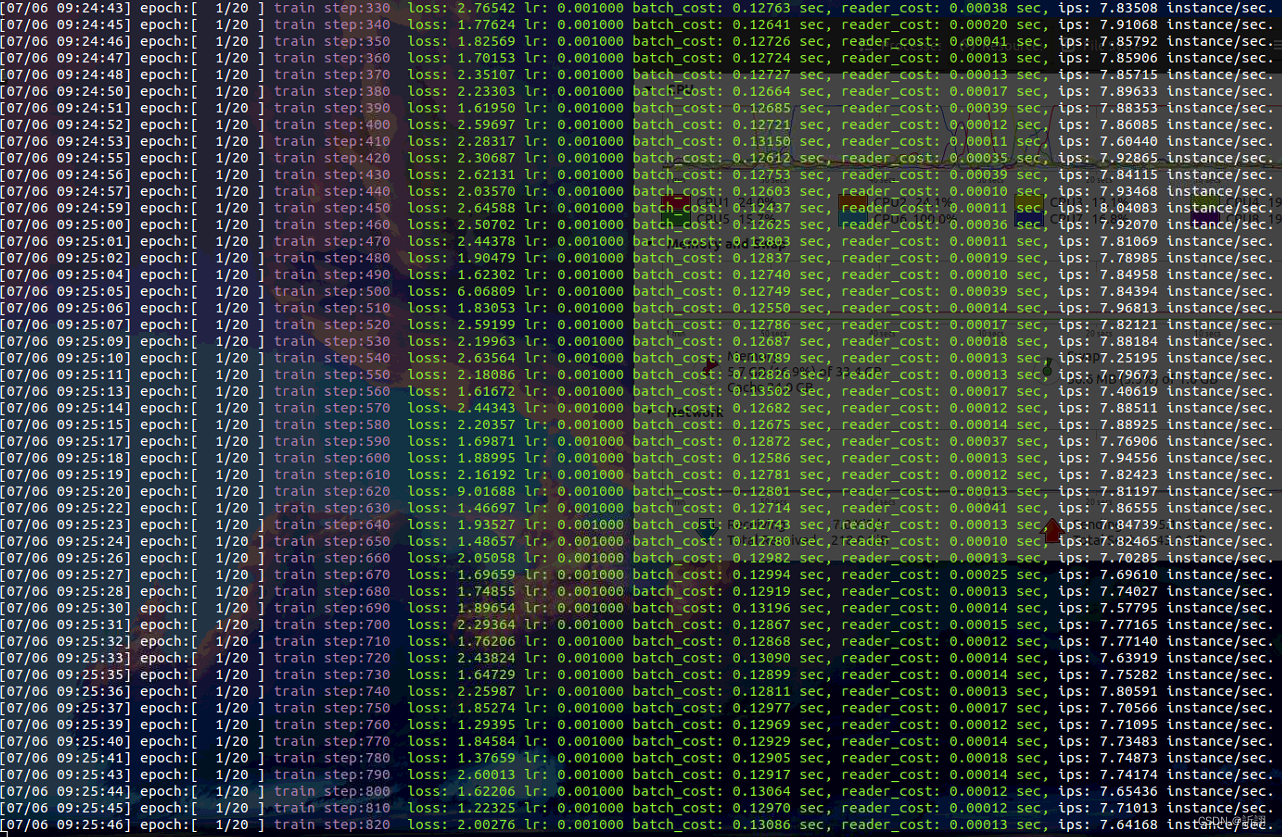
Baidu flying general BMN timing action positioning framework | data preparation and training guide (Part 2)

新工作感悟~辞旧迎新~
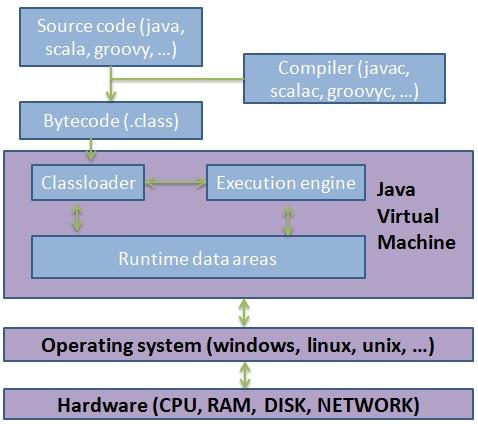
JVM 内存模型
云呐|工单管理软件,工单管理软件APP

Byte P7 professional level explanation: common tools and test methods for interface testing, Freeman
Appium foundation - appium inspector positioning tool (I)
According to the analysis of the Internet industry in 2022, how to choose a suitable position?
随机推荐
What does security capability mean? What are the protection capabilities of different levels of ISO?
The cradle of eternity
Yunna | work order management measures, how to carry out work order management
Make Jar, Not War
2022 Google CTF SEGFAULT LABYRINTH wp
Reptile practice (VI): novel of climbing pen interesting Pavilion
Telnet,SSH1,SSH2,Telnet/SSL,Rlogin,Serial,TAPI,RAW
New job insights ~ leave the old and welcome the new~
今日问题-2022/7/4 lambda体中修改String引用类型变量
JS reverse -- ob confusion and accelerated music that poked the [hornet's nest]
Vocabulary in Data Book
JVM 内存模型
Typical problems of subnet division and super network construction
Box stretch and pull (left-right mode)
Taro applet enables wxml code compression
一起看看matlab工具箱内部是如何实现BP神经网络的
Yunna - work order management system and process, work order management specification
修改px4飞控的系统时间
初识MySQL
Yunna | work order management software, work order management software app