当前位置:网站首页>【LeetCode】106. Construct binary tree from middle order and post order traversal sequence (wrong question 2)
【LeetCode】106. Construct binary tree from middle order and post order traversal sequence (wrong question 2)
2022-07-05 02:20:00 【Kaimar】
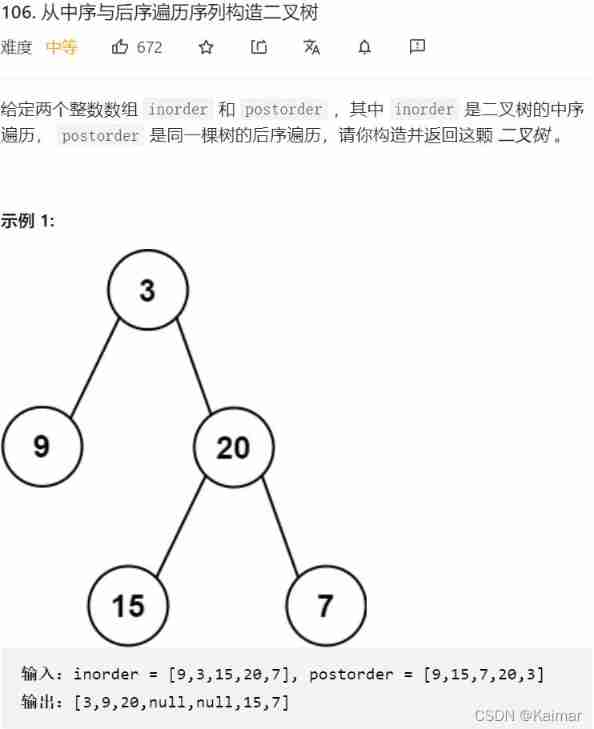

- Ideas
The result of middle order traversal is different from that of pre order traversal 、 Post order traversal for combination , Can uniquely identify a tree , Using traversal results to construct a tree is to do segmentation , Middle order and post order traversal combination , Determine the current node through the reverse order of post order traversal , Then divide the middle order to determine the left and right subtrees , Such as 3 Is divided into [9],[15, 20, 7] Respectively 3 Right and left subtrees .
Or recursion , So there is a recursive trilogy ( Write a version of the code and make mistakes , It was an error in cutting , It's better to recurse without knowing how to cut , Refer to the explanation of the question )
There are six steps in total :
First step : If the array size is zero , It indicates that the node is empty .
The second step : If it's not empty , Then take the last element of the subsequent array as the node element .
The third step : Find the position of the last element of the ordered array in the ordered array , As a cutting point
Step four : Cut the ordered array , Cut into middle order left array and middle order right array ( Don't reverse the order , It must be the first to cut the ordered array )
Step five : Cut sequential array , Cut into the left array and the right array
Step six : Recursively handle left and right intervals
The difficulty lies in how to cut , It is necessary to unify the opening and closing of the left and right , Then there is how to cut the sequence , How to find the cutting point of the subsequent array ?
There is no explicit cutting element in the subsequent array to cut left and right , Unlike a mid order array, there are clear cut points , Just separate the cutting points left and right .
At this point, there is a very heavy point , That is, the size of the middle order array must be the same as that of the later order array ( This is inevitable ).
- summary
This problem knows that thinking and writing code are two different things , There are still many difficulties in writing code , One is when to return , The second is how to split the middle order and post order arrays , The third is the segment details .
/** * Definition for a binary tree node. * type TreeNode struct { * Val int * Left *TreeNode * Right *TreeNode * } */
func buildTree(inorder []int, postorder []int) *TreeNode {
// 1. Array is empty , Null node
nLen := len(inorder)
if nLen == 0 {
return nil
}
// 2. Not empty , Then the last node of post order traversal is taken as the root node
// A special case , Only one is leaf node , Go straight back to
root := &TreeNode{
Val : postorder[nLen - 1],
Left : nil,
Right : nil,
}
if nLen == 1 {
return root
}
// 3. Find the split point in the middle order traversal
var i int
for i = 0; i < nLen; i++ {
if inorder[i] == postorder[nLen - 1] {
break
}
}
// 4. Divide the middle order traversal array
// [0, i)
leftInorder := inorder[:i]
// [i + 1, len(inorder))
rightInorder := inorder[i + 1 :]
// 5. After splitting, traverse the array
// Lose the last
postorder = postorder[: len(postorder) - 1]
// Find the dividing point through the length
point := len(leftInorder)
// [0, point)
leftPostorder := postorder[: point]
// [point, len(postorder))
rightPostorder := postorder[point : ]
// 6. Recursion goes to the next level
root.Left = buildTree(leftInorder, leftPostorder)
root.Right = buildTree(rightInorder, rightPostorder)
return root
}

边栏推荐
- Security level
- Blue bridge - maximum common divisor and minimum common multiple
- STL container
- Chinese natural language processing, medical, legal and other public data sets, sorting and sharing
- Yolov5 model training and detection
- Win:将一般用户添加到 Local Admins 组中
- One plus six brushes into Kali nethunter
- Can you really learn 3DMAX modeling by self-study?
- Data guard -- theoretical explanation (III)
- MATLB | multi micro grid and distributed energy trading
猜你喜欢
The most powerful new household god card of Bank of communications. Apply to earn 2100 yuan. Hurry up if you haven't applied!
R language uses logistic regression and afrima, ARIMA time series models to predict world population

【附源码】基于知识图谱的智能推荐系统-Sylvie小兔
Icu4c 70 source code download and compilation (win10, vs2022)
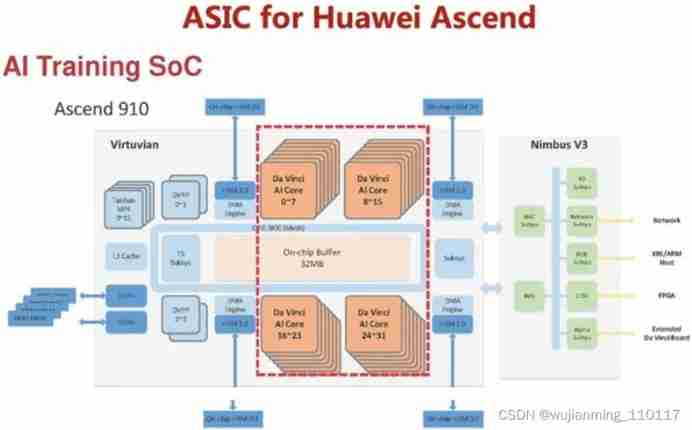
Traditional chips and AI chips

The perfect car for successful people: BMW X7! Superior performance, excellent comfort and safety
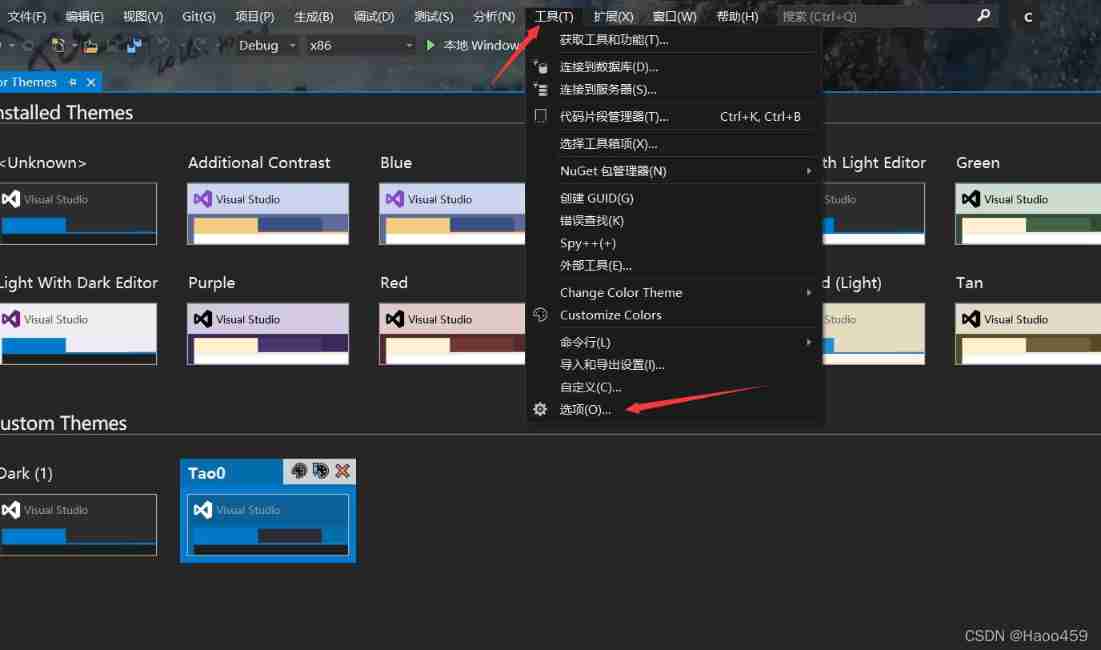
Visual studio 2019 set transparent background (fool teaching)
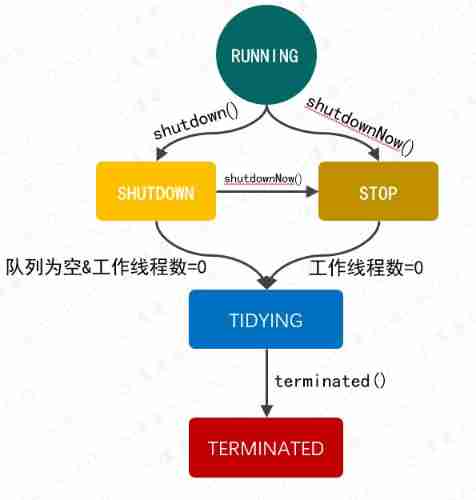
Write a thread pool by hand, and take you to learn the implementation principle of ThreadPoolExecutor thread pool
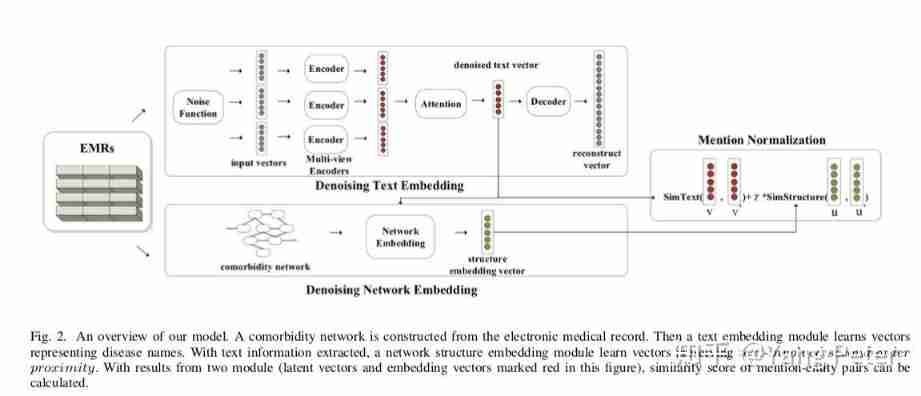
Exploration of short text analysis in the field of medical and health (II)
PowerShell:在代理服务器后面使用 PowerShell
随机推荐
A tab Sina navigation bar
Pytorch common code snippet collection
Bert fine tuning skills experiment
Luo Gu Pardon prisoners of war
Grub 2.12 will be released this year to continue to improve boot security
Write a thread pool by hand, and take you to learn the implementation principle of ThreadPoolExecutor thread pool
Chinese natural language processing, medical, legal and other public data sets, sorting and sharing
openresty ngx_lua执行阶段
A label making navigation bar
Naacl 2021 | contrastive learning sweeping text clustering task
Application and Optimization Practice of redis in vivo push platform
Timescaledb 2.5.2 release, time series database based on PostgreSQL
Interesting practice of robot programming 14 robot 3D simulation (gazebo+turtlebot3)
Redis' hyperloglog as a powerful tool for active user statistics
Video display and hiding of imitation tudou.com
172. Zero after factorial
Missile interception -- UPC winter vacation training match
Grpc message sending of vertx
The perfect car for successful people: BMW X7! Superior performance, excellent comfort and safety
100 basic multiple choice questions of C language (with answers) 04