当前位置:网站首页>曼哈顿距离和-打印菱形
曼哈顿距离和-打印菱形
2022-07-06 06:01:00 【starnight531】
食用指南:
Leetcode专栏开启了,由于博主闭关期末,所以每日只能一题尽量做到一题多解,先说思路,之后代码实现,会添加必要注释语法或STL内容会在注意点中点出,新手友好欢迎关注博主神机百炼专栏,内涵算法基础详细讲解和代码模板
题目描述:
输入一个奇数 n,输出一个由 * 构成的 n 阶实心菱形。
输入格式
一个奇数 n。输出格式
输出一个由 * 构成的 n 阶实心菱形。具体格式参照输出样例。
数据范围
1≤n≤99
输入样例:
5
输出样例:
题目来源:https://www.acwing.com/problem/content/729/
题目分析:
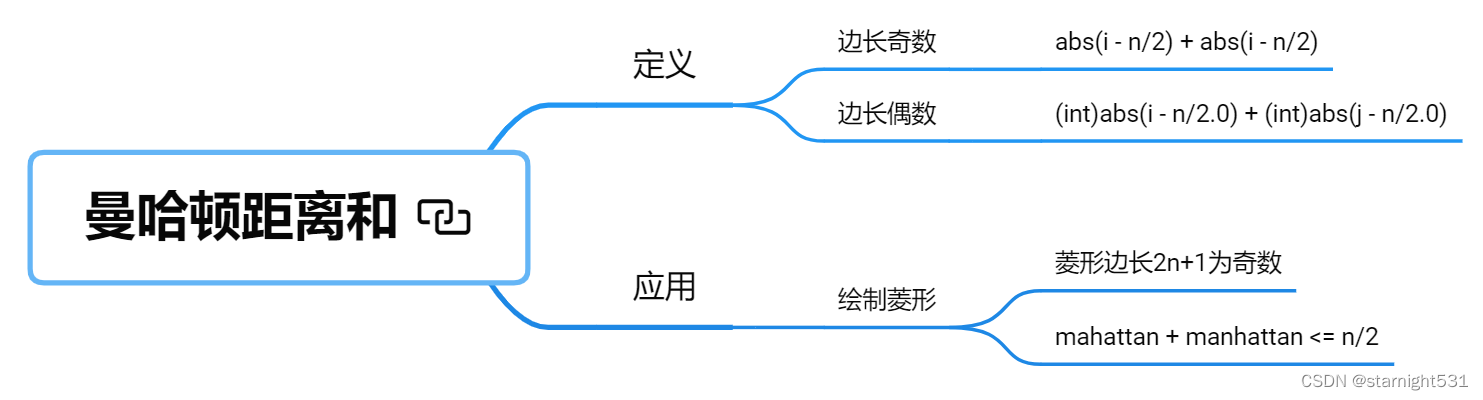
法一:曼哈顿距离和:
曼哈顿距离:x / y 方向投影距离的最大值
曼哈顿距离和:x 方向投影距离 + y方向投影距离
菱形:
圆本身的性质为各点到圆心的距离相等,这个距离是根号下((Δx)2+(Δy)2)
在数组中,由于精度问题,将距离化简为曼哈顿距离和
相同的曼哈顿距离和的点的集合形成的是一个菱形,菱形已经很逼近
但是由于本身数学表达式不同,所得的图形再像也是一个菱形
算法模板:
代码实现:
法一:
- 只输入奇数:
import java.util.Scanner;
import java.lang.Math;
public class Main{
public static void main(String[] args){
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
for(int i=0; i<n; i++){
for(int j=0; j<n; j++){
if (Math.abs(i - n/2)+Math.abs(j - n/2) <= n/2){
System.out.print("*");
}else System.out.print(" ");
}
System.out.println();
}
}
}
- 奇偶混合输入:
import java.util.Scanner;
import java.lang.Math;
public class Main{
public static void main(String[] args){
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int m = n;
if (n % 2 == 0) m++;
for(int i=0; i<m; i++){
for(int j=0; j<m; j++){
if (Math.abs(i - m/2)+Math.abs(j - m/2) <= m/2){
System.out.print("*");
}else System.out.print(" ");
}
System.out.println();
}
}
}
注意点:
对于奇数行菱形:
输入n既是菱形一共的行数列数,又是菱形中间行的*个数
菱形外侧正方形行数/列数都是奇数,中点为 (n/2 , n/2),mahattan = max(abs(i - n/2), abs(j - n/2))
对于偶数行菱形:
输入n为偶数,而菱形行数列数为n+1,中间行*个数也是n+1
菱形外侧正方形行数/列数都是奇数,中点为((n+1/2), (n+1)/2),mahattan = max(abs(i - (n+1)/2), abs(j - (n+1)/2))
能不能强制利用偶数的曼哈顿距离公式求解?
答案是这个题不能,毕竟画菱形只能奇数行奇数列(2*n + 1),
强制用偶数曼哈顿距离公式求解出来的中点其实不是中点,距离更是错误。示范:下列代码输入4所绘制的菱形为
import java.util.Scanner;
import java.lang.Math;
public class Main{
public static void main(String[] args){
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int m = n;
if (n % 2 == 0) m++;
for(int i=0; i<m; i++){
for(int j=0; j<m; j++){
//偶数想用曼哈顿距离公式就是错的,中点位置和距离都错
if(n % 2 == 1){
if (Math.abs(i - n/2)+Math.abs(j - n/2) <= n/2){
System.out.print("*");
}else System.out.print(" ");
}else{
if ((int)Math.abs(i - (n-1)/2.0)+(int)Math.abs(j - (n-1)/2.0) <= n/2){
System.out.print("*");
}else System.out.print(" ");
}
}
System.out.println();
}
}
}

边栏推荐
- Redistemplate common collection instructions opsforvalue (II)
- The difference and usage between continue and break
- 【C语言】字符串左旋
- IP day 16 VLAN MPLS configuration
- Zoom through the mouse wheel
- Seven imperceptible truths in software testing
- 公司視頻加速播放
- C language learning notes (mind map)
- Linux regularly backs up MySQL database
- [untitled]
猜你喜欢

HCIA review
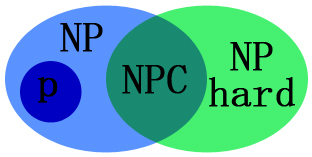
P问题、NP问题、NPC问题、NP-hard问题详解

The ECU of 21 Audi q5l 45tfsi brushes is upgraded to master special adjustment, and the horsepower is safely and stably increased to 305 horsepower
【API接口工具】postman-界面使用介绍

Grant Yu, build a web page you want from 0
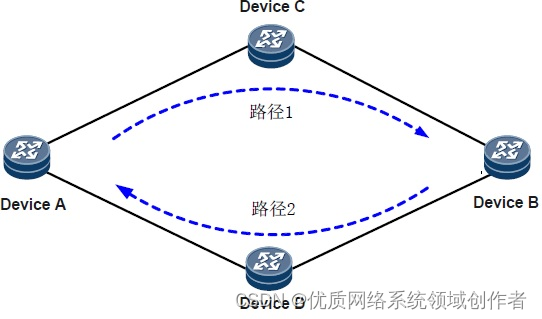
Huawei BFD configuration specification

Wib3.0 leapfrogging, in leapfrogging (ง • ̀_•́) ง
Embedded point test of app

MIT6.s081-2020 Lab2 System Calls
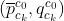
VINS-Mono: A Robust and Versatile Monocular Visual-Inertial State Estimator
随机推荐
The ECU of 21 Audi q5l 45tfsi brushes is upgraded to master special adjustment, and the horsepower is safely and stably increased to 305 horsepower
[untitled]
Caused by:org.gradle.api.internal.plugins . PluginApplicationException: Failed to apply plugin
As3013 fire endurance test of cable distribution system
数学三大核心领域概述:代数
CoDeSys note 2: set coil and reset coil
华为路由器忘记密码怎么恢复
MPLS test report
Significance of unit testing
公司视频加速播放
GTSAM中李群的運用
Li Chuang EDA learning notes 12: common PCB board layout constraint principles
HCIA复习
数字三角形模型 AcWing 1015. 摘花生
Cannot build artifact 'test Web: War expanded' because it is included into a circular depend solution
2022 software testing workflow to know
My 2021
Eigen稀疏矩阵操作
Leetcode 701 insertion operation in binary search tree -- recursive method and iterative method
Introduction to promql of # yyds dry goods inventory # Prometheus