当前位置:网站首页>Data processing methods - smote series and adasyn
Data processing methods - smote series and adasyn
2022-07-06 04:09:00 【Code Taoist】
brief introduction
Unbalanced dataset refers to the extremely unbalanced sample size of each category of the dataset . A case study of dichotomous problems , Suppose that the number of samples of the positive class is much larger than that of the negative class , Usually, the proportion of most samples is close to 100:1 The data in this case is called unbalanced data . The learning of unbalanced data requires learning useful information in unevenly distributed data sets .
The processing methods of unbalanced data sets are mainly divided into two aspects :
1、 From a data perspective , The main method is sampling , It is divided into undersampling and oversampling and some corresponding improvement methods .
2、 From the perspective of Algorithm , Considering the cost difference of different misclassification cases, the algorithm is optimized , Mainly based on cost sensitive learning algorithm (Cost-Sensitive Learning), The representative algorithms are adacost;
In addition, the problem of unbalanced data sets can be considered as a classification (One Class Learning) Or anomaly detection (Novelty Detection) problem , The representative algorithms are One-class SVM.
SMOTE series
SMOTE
SMOTE(Synthetic Minority Oversampling Technique) Synthesis of a few oversampling techniques , It is an over sampling algorithm improved on the basis of random sampling . Select a sample from a few samples xi. secondly , By sampling magnification N, from xi Of K Random selection among nearest neighbors N Samples xzi. Last , In turn, it's xzi and xi Randomly synthesize new samples , The synthesis formula is as follows :
$$xn=xi+beta(x{zi}-xi)$$
Address of thesis
SMOTE: Synthetic Minority Over-sampling Technique
Borderline SMOTE
Borderline SMOTE Is in SMOTE Based on the improved oversampling algorithm , The algorithm only uses a few class samples on the boundary to synthesize new samples , So as to improve the category distribution of samples .
Borderline SMOTE The sampling process is to divide a small number of samples into 3 class , Respectively Safe、Danger and Noise,Safe, More than half of the samples are minority samples ;Danger: More than half of the samples around are most types of samples , As a sample on the boundary ;Noise: The samples are surrounded by most types of samples , Considered noise , As shown in the middle of the picture C Last , For tables only Danger A few classes of samples are oversampled .
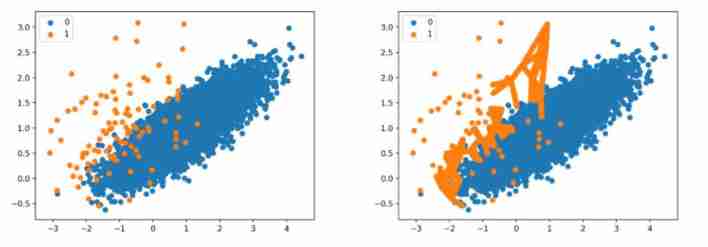
Address of thesis
Borderline-SMOTE: A New Over-Sampling Method in Imbalanced Data Sets Learning
ADASYN series
ADASYN
ADASYN (adaptive synthetic sampling) Adaptive synthetic sampling , And Borderline SMOTE be similar , Give different weights to different minority samples , So as to generate different numbers of samples .
step
- Calculate the number of samples to be synthesized , The formula is as follows :
$$G=left(m{l}-m{s}right) times beta$$
among , $m{text { 丨 }}$ Number of samples for most classes , $m{s}$ Is the number of samples of a few classes , $beta in[0,1]$ random number , if $beta$ be equal to 1 , The positive and negative ratio after sampling is $1: 1$ .
- Calculation K Most classes in the nearest neighbors account for , The formula is as follows :
$$r{i}=Delta{i} / K$$
among , $Delta{i}$ by $K$ Number of samples of most classes in nearest neighbors , $i=1,2,3, ldots ldots, m{s}$
- Yes ri Standardization , The formula is as follows :
$$hat{r}{i}=r{i} / sum{i=1}^{m{s}} r_{i}$$
- According to the sample weight , Calculate the number of new samples to be generated for each minority sample , The formula is as follows :
$$g=hat{r}_{i} times G$$
- according to $g$ Calculate the number of samples to be generated for each small number of samples , according to SMOTE The algorithm generates samples , The formula is as follows :
$$s{i}=x{i}+left(x{z i}-x{i}right) times lambda$$
among , $mathrm{s}{i}$ For synthetic samples , $mathrm{x}{i}$ It is the second in a few samples $i$ Samples , $mathrm{x}{mathrm{z} i}$ yes $mathrm{x}{mathrm{i}}$ Of K Randomly select a minority sample from the nearest neighbors $lambda in[0,1]$ The random number .
Address of thesis
ADASYN: Adaptive Synthetic Sampling Approach for Imbalanced Learning
边栏推荐
- 【FPGA教程案例11】基于vivado核的除法器设计与实现
- [introduction to Django] 11 web page associated MySQL single field table (add, modify, delete)
- Oracle ORA error message
- Simple blog system
- C mouse event and keyboard event of C (XXVIII)
- Fundamentals of SQL database operation
- Stack and queue
- Global and Chinese markets for patent hole oval devices 2022-2028: Research Report on technology, participants, trends, market size and share
- 图应用详解
- MySql數據庫root賬戶無法遠程登陸解决辦法
猜你喜欢
关于进程、线程、协程、同步、异步、阻塞、非阻塞、并发、并行、串行的理解
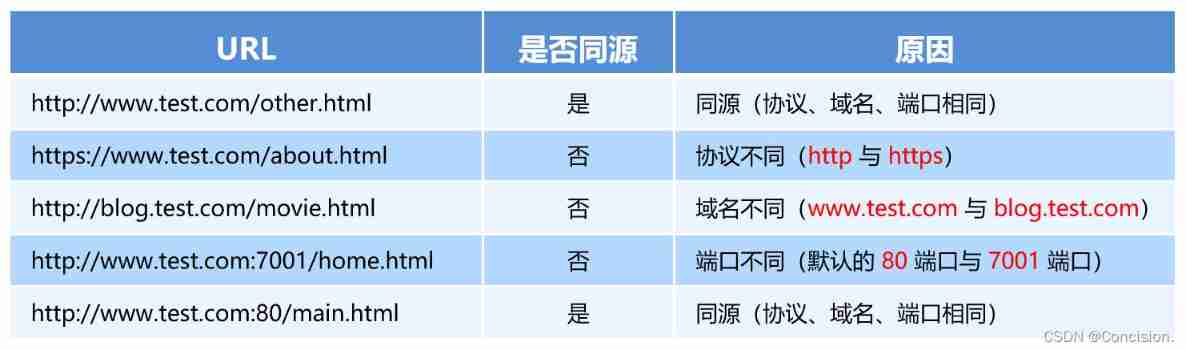
Cross domain and jsonp details
Redis (replicate dictionary server) cache
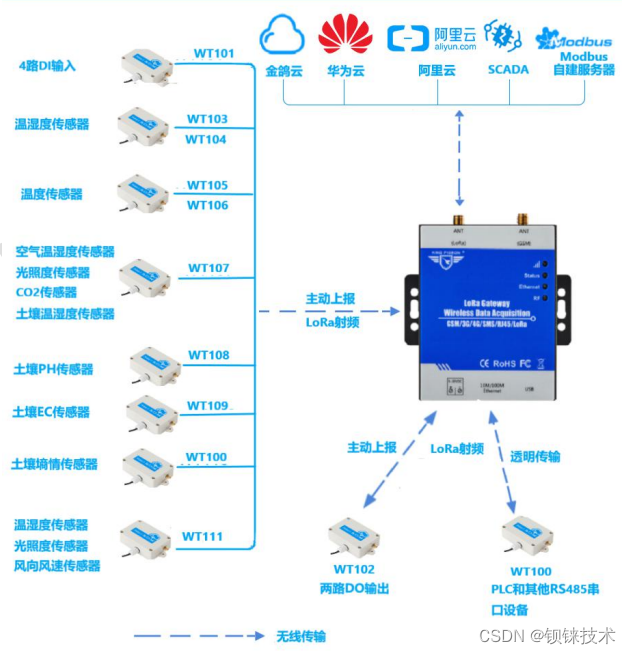
lora网关以太网传输
![[PSO] Based on PSO particle swarm optimization, matlab simulation of the calculation of the lowest transportation cost of goods at material points, including transportation costs, agent conversion cos](/img/41/27ce3741ef29e87c0f3b954fdef87a.png)
[PSO] Based on PSO particle swarm optimization, matlab simulation of the calculation of the lowest transportation cost of goods at material points, including transportation costs, agent conversion cos
Basic use of MySQL (it is recommended to read and recite the content)
DM8 backup set deletion

STC8H开发(十二): I2C驱动AT24C08,AT24C32系列EEPROM存储
Error 1045 (28000): access denied for user 'root' @ 'localhost' (using password: no/yes
MySql數據庫root賬戶無法遠程登陸解决辦法
随机推荐
【FPGA教程案例11】基于vivado核的除法器设计与实现
In Net 6 CS more concise method
Interface idempotency
Mathematical modeling regression analysis relationship between variables
Record the pit of NETCORE's memory surge
Le compte racine de la base de données MySQL ne peut pas se connecter à distance à la solution
Prime protocol announces cross chain interconnection applications on moonbeam
Alibaba testers use UI automated testing to achieve element positioning
2/11 matrix fast power +dp+ bisection
Hashcode and equals
Class A, B, C networks and subnet masks in IPv4
Global and Chinese markets for patent hole oval devices 2022-2028: Research Report on technology, participants, trends, market size and share
记一次excel XXE漏洞
math_ Derivative function derivation of limit & differential & derivative & derivative / logarithmic function (derivative definition limit method) / derivative formula derivation of exponential functi
深入浅出node模板解析错误escape is not a function
User datagram protocol UDP
MySQL master-slave replication
Determine which week of the month the day is
AcWing 243. A simple integer problem 2 (tree array interval modification interval query)
Path of class file generated by idea compiling JSP page