[Jianzhi offer] 6-10 questions

Print linked list from end to end

The finger of the sword Offer 06. Print linked list from end to end - Power button （LeetCode）

From the end to the end , You can change the point to , But it's more troublesome , And also changed the structure of the linked list .

Observe the structure of the print , Print the tail first and then print the head , It is very similar to the structure of stack , So use stack to write .

class Solution {
public:
    vector<int> reversePrint(ListNode* head) {
        stack<int> st;
        vector<int>ret;
        ListNode* cur=head;
        while(cur!=NULL)
        {
            st.push(cur->val);
            cur=cur->next;
        }
        int sz=st.size();
        ret.resize(sz);
        for(int i=0;i<sz;i++)
        {
            ret[i]=st.top();
            st.pop();
        }
        return ret;
    }
};

Reconstruction of binary tree

The finger of the sword Offer 07. Reconstruction of binary tree - Power button （LeetCode）

The idea of building a tree ： The first node of the preamble sequence must be the root node , All nodes on the left of the root node in the middle order sequence are left subtrees , The ones on the right are all right subtrees , The specific measures will not be repeated . The following is an analysis from the perspective of code implementation

The difficulty of this problem is to determine the benchmark and the parameters of the recursive function , In fact, the interval is easy to calculate .

Determining the benchmark means whether the subscript position of the elements I use is based on the middle order sequence or the previous order sequence .

Next, I use the position of the root node as the benchmark of the preorder sequence , So in the parameters of recursive function pre_root It represents the position of the root node of the current tree in the previous sequence ,in_root and in_right It represents the left and right boundaries of this tree in the middle order sequence .

class Solution {
public:
    //TreeNode* _bulidTree(TreeNode* root,int left,int right)//root If not int You cannot determine the position of the root node in the preorder traversal sequence 
    TreeNode* _bulidTree(int pre_root,int in_left,int in_right)
    {
        if(in_left>in_right)// It shows that the left and right subtrees corresponding to this node are unreasonable 
        {
            return NULL;
        }
        TreeNode* root=new TreeNode(preorder[pre_root]);// Create a root node 
        int x=find(inorder.begin(),inorder.end(),preorder[pre_root])-inorder.begin();// Find the position of the root node in the middle order sequence 
        int l_length=x-in_left;// The length of the left section 
        int r_length=in_right-x;// The length of the right section 
        root->left=_bulidTree(pre_root+1,in_left,in_left+l_length-1);// Build the left subtree 
        root->right=_bulidTree(pre_root+l_length+1,in_right-r_length+1,in_right);// Build the right subtree 
        return root;
    }
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        this->preorder=preorder;// Let the subfunction _buildTree You can get preorder
        this->inorder=inorder;// Empathy 
        TreeNode* root=_bulidTree(0,0,preorder.size()-1);// Both sides of my interval are closed 
        return root;
    }
private:
    vector<int> preorder;
     vector<int> inorder;
};

This code also has an optimization point , Careful observation shows that every recursion I have to calculate the position of the root node in the middle order sequence , and find The bottom of the is to find one by one , The efficiency is not high , So here we can use the idea of hash to map the position of the root node in the middle order sequence .

class Solution {
public:
    //TreeNode* _bulidTree(TreeNode* root,int left,int right)//root If it is not for shaping, the position of the root node in the preorder traversal sequence cannot be determined 
    TreeNode* _bulidTree(int pre_root,int in_left,int in_right)
    {
        if(in_left>in_right)
        {
            return NULL;
        }
        TreeNode* root=new TreeNode(preorder[pre_root]);
       // int x=find(inorder.begin(),inorder.end(),preorder[pre_root])-inorder.begin();
        int l_length=dic[preorder[pre_root]]-in_left;// The length of the left section 
        int r_length=in_right-dic[preorder[pre_root]];// The length of the right section 
        root->left=_bulidTree(pre_root+1,in_left,in_left+l_length-1);
        root->right=_bulidTree(pre_root+l_length+1,in_right-r_length+1,in_right);
        return root;
    }
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        this->preorder=preorder;
        for(int i=0;i<inorder.size();i++)
        {
            dic[inorder[i]]=i;// Subscripts of ordered sequence elements in mapping 
        }
        TreeNode* root=_bulidTree(0,0,preorder.size()-1);
        return root;
    }
private:
    vector<int> preorder;
    vector<int> inorder;
    unordered_map<int,int>dic;// Dictionaries , Represents a mapping relationship 
};

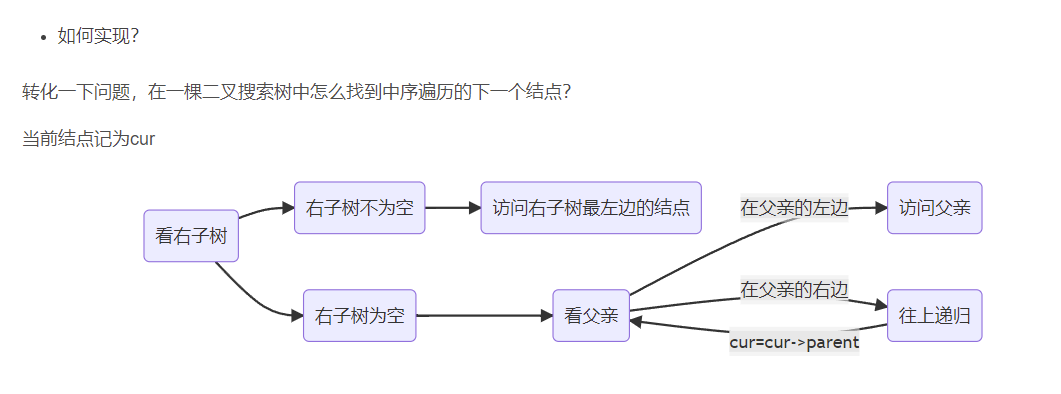
The next node of a binary tree

There is no link found in this question

Find the next node of the middle order traversal

I used to write about red and black trees ++ I wrote something similar , Here, paste the code at that time , The details are as follows （ This picture is the content of my red black tree blog ）

self& operator++()// In front of ++
{
    
    Node* cur = _node;
    if (cur->_right)
    {
    
        // The right subtree is not empty , You can't directly give the root of the right subtree to _node
        // Because the leftmost leaf of the right subtree is the next node that should be accessed 
        Node* right = cur->_right;
        while (right&&right->_left)
        {
    
            right = right->_left;
        }
        _node = right;
        return *this;
    }
    else// The right subtree is empty 
        // Look at my father 
    {
    
        Node* parent = cur->_parent;
        while (parent&&parent->_right == cur)
        {
    
            cur = parent;
            parent = cur->_parent;
        }
        if (parent == nullptr)
        {
    
            _node = nullptr;
        }
        else
        {
    
            _node = parent;
        }

        return *this;
    }
}

Queues are implemented with two stacks

The finger of the sword Offer 09. Queues are implemented with two stacks - Power button （LeetCode）

Use two stacks to simulate the implementation of queues .

Pay special attention to the empty stack , If you don't handle the empty stack, you can't compile it （VS Run too fast ）

class CQueue {
public:
    CQueue() {}
  
    void appendTail(int value) {
        st1.push(value);
    }
    
    int deleteHead() {
        if(st1.empty()&&st2.empty())// Consider the case that both stacks are empty , because _ move Empty stack is not handled 
        // If both incoming stacks are empty , It can lead to stack An error is reported when accessing the data at the top of the stack when it is empty 
        {
            return -1;
        }
        _move(st1,st2);
        int x=st2.top();
        st2.pop();
        _move(st2,st1);
        return x;
    }
    void _move(stack<int>&s1,stack<int>&s2)// hold s1 Move your data to s2 Inside 
    {
        while(!s1.empty())
        {
            s2.push(s1.top());
            s1.pop();
        }
    }
private:
    stack<int>st1;
    stack<int>st2;
};

Fibonacci sequence

The finger of the sword Offer 10- I. Fibonacci sequence - Power button （LeetCode）

According to the formula given by the topic, you can recurse .

class Solution {
public:
    int fib(int n) {       
        if(n==0)
        {
            return 0;
        } 
        else if(n==1) 
        {
            return 1;
        }
        else
        {
            int pprev=0;// Previous to current number 
            int prev=1;// The previous of the current number 
            for(int i=2;i<=n;i++)
            {
                int tmp=(prev+pprev)%1000000007;
                pprev=prev%1000000007;
                prev=tmp;
            }
            return prev;// The result of the last calculation is tmp Give it to prev
        }
    }
};

There is also a kind of logn Solution method , But it's complicated to write , Not enough practical .

【 Expand 】 Frogs jump the steps

The finger of the sword Offer 10- II. The problem of frog jumping on the steps - Power button （LeetCode）

Fibonacci's deformation , It can also be used. dp To do .

Remember the frog jumping on the first n The number of schemes for the ladder is dp[n]; be dp[n]=dp[n-1]+dp[n-2]; For example, the frog is in the first N Steps , Then it can only be from N-1 Or N-2 Up the grade

class Solution {
    
public:
    int numWays(int n) {
    
        int a[]={
    1,1};
        if(n<2)
        {
    
            return a[n];
        }
        int ans=0;
        int pprev=1;
        int prev=1;
        for(int i=2;i<=n;i++)
        {
    
            ans=(pprev+prev)%1000000007;
            pprev=prev%1000000007;
            prev=ans;
        }
        return ans;
    }
};

【 Expand 】 Rectangular overlay

No link found for this question … But it is also Fibonacci's deformation .