当前位置：网站首页>A Cooperative Approach to Particle Swarm Optimization

A Cooperative Approach to Particle Swarm Optimization

2022-07-06 01:24:00 【Figure throne】

0、 Background

CPSO It's based on standards PSO Deformed from , This paper presents a new method of PSO Variants of the algorithm , Called collaborative particle swarm optimizer , or CPSO. Using cooperative behavior to significantly improve the performance of the original algorithm , This is achieved by using multiple groups to jointly optimize the different components of the solution vector .

Van den Bergh F, Engelbrecht A P. A cooperative approach to particle swarm optimization[J]. IEEE transactions on evolutionary computation, 2004, 8(3): 225-239.

1、CPSO

1.1 standard PSO

of PSO Algorithm and specific implementation , See my previous blog ： standard PSO.

Speed update formula ：

$\begin{aligned} v_{i, j}(t+1)=w v_{i, j}(t)+c_{1} r_{1, i}(t) & {\left[y_{i, j}(t)-x_{i, j}(t)\right] } +c_{2} r_{2, i}(t)\left[\hat{y}_{j}(t)-x_{i, j}(t)\right] &(1)\end{aligned}$

Position update formula ：

$\mathbf{x}_{i}(t+1)=\mathbf{x}_{i}(t)+\mathbf{v}_{i}(t+1)(2)$

pbest Update formula ：

$\mathbf{y}_{i}(t+1)=\left\{\begin{array}{ll} \mathbf{y}_{i}(t), & \text { if } f\left(\mathbf{x}_{i}(t+1)\right) \geq f\left(\mathbf{y}_{i}(t)\right) \\ \mathbf{x}_{i}(t+1), & \text { if } f\left(\mathbf{x}_{i}(t+1)\right)<f\left(\mathbf{y}_{i}\right)(t) \end{array}\right.(3)$

gbest Update formula ：

$\hat{\mathbf{y}}(t+1)=\arg \min _{\mathbf{y}_{i}} f\left(\mathbf{y}_{i}(t+1)\right), \quad 1 \leq i \leq s$

1.2 CPSO_Sk

CPSO The algorithm decomposes the larger search space into several smaller spaces , Therefore, each subgroup converges to the solution contained in its subspace significantly faster than the standard PSO In primitive n Convergence rate on dimensional search space .

If each subspace dimension is set to 1 dimension , So the whole n Dimensional space is divided into n individual 1 The subspace of dimension .

$p_{j}$ It means s*1 Dimensional sample subspace ,s Represents the total number of particles ,1 representative n One dimensional variable in dimension .
$p_{j}.x_{i}$ On behalf of the j In the subspace i The position of a particle .
$p_{j}.y_{i}$ On behalf of the j In the subspace i Of particles pbest.
$p_{j}.\hat{y}$ On behalf of the j Subspace gbest.
This function returns a n Dimension vector , By connecting all the global best vectors of all subspaces , Except for j Weight , It is replaced by z.

If each subspace dimension is set to k dimension , So the whole n Dimensional space is divided into $\left \lceil n/k \right \rceil$ individual k The subspace of dimension .

1.3 CPSO_Hk

In the previous section ,CPSO_Sk The algorithm is easy to fall into the local optimal position of subspace , Global search capability compared to PSO Declined . In order to improve the CPSO_Sk Global search capability , take CPSO_Sk and PSO Combine , To form the CPSO_Hk Algorithm .

P and Q The total number of populations is s, here P and Q The population number of is set to s/2.
k Is a sample of a randomly selected population , And carry on Q and P The corresponding information interaction between populations .

1.4 Algorithm reproduction and experiment

The algorithm experiment in this article is complex , I don't intend to reproduce it according to the ideas in the article . Here I reproduce the algorithm and carry out simple experiments , See if there are any effects , If effective, it is convenient to apply its ideas to other places . Therefore, the recurrence of this article only stays in the understanding and reference of thought .

PSO( Repeat the experiment 100 Time , Average. )：

function f = Rastrigin(x)
% the Rastrigin function
% xi = [-5.12,5.12]
d = size(x,2);
f = 10*d + sum(x.^2 - 10*cos(2*pi*x),2);
end

clc;clear;clearvars;
%  Random generation 5 Data 
num_initial = 20;
num_vari = 60;
%  Search range 
upper_bound = 5.12;
lower_bound = -5.12;
iter = 12000;
w = 1;
%  Random generation 5 Data , And obtain its evaluation value 
sample_x = lhsdesign(num_initial, num_vari).*(upper_bound - lower_bound) + lower_bound.*ones(num_initial, num_vari);
sample_y = Rastrigin(sample_x);
Fmin = zeros(iter, 1);
aver_Fmin = zeros(iter, 1);

for n = 1 : 100
    k = 1;
    %  Initialize some parameters 
    pbestx = sample_x;
    pbesty = sample_y;
    %  Current location information presentx
    presentx = lhsdesign(num_initial, num_vari).*(upper_bound - lower_bound) + lower_bound.*ones(num_initial, num_vari);
    vx = sample_x;
    [fmin, gbest] = min(pbesty);
    fprintf("n: %.4f\n", n);
    % fprintf("iter 0 fmin: %.4f\n", fmin);
    for i = 1 : iter
        r = rand(num_initial, num_vari);
        % pso Update the location of the next step , Here you can set the boundary if it exceeds the search range 
        vx = w.*vx + 2 * r .* (pbestx - presentx) + 2 * r .* (pbestx(gbest, :) - presentx);
        vx(vx > upper_bound) = upper_bound;
        vx(vx < lower_bound) = lower_bound;
        presentx = presentx + vx;
        presentx(presentx > upper_bound) = upper_bound;
        presentx(presentx < lower_bound) = lower_bound;
        presenty = Rastrigin(presentx);
        %  Update the best location for each individual 
        pbestx(presenty < pbesty, :) = presentx(presenty < pbesty, :);
        pbesty(presenty < pbesty, :) = presenty(presenty < pbesty, :);
        %  Update the best location of all individuals 
        [fmin, gbest] = min(pbesty);
        % fprintf("iter %d fmin: %.4f\n", i, fmin);
        Fmin(k, 1) = fmin;
        k = k +1;
    end
    aver_Fmin = aver_Fmin + Fmin;
end
aver_Fmin = aver_Fmin ./ 100;
% disp(pbestx(gbest, :));
plot(aver_Fmin);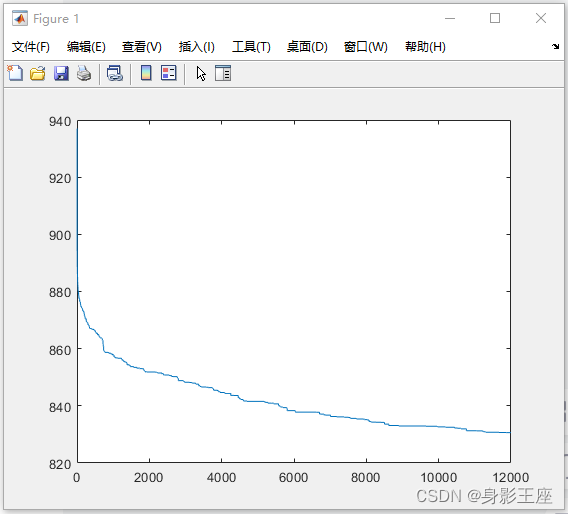

CPSO_Sk( Repeat the experiment 100 Time , Average. ):

clc;clear;clearvars;
%  Random generation 20 Data 
num_initial = 20;
num_vari = 60;
%  Search range 
upper_bound = 5.12;
lower_bound = -5.12;
%  Calculate during iteration y Total number of values 
eval_num = 12000;
% K Represents the number of partitioned subspaces ,sub_num Represents the dimension of each subspace 
K = 5;
sub_num = num_vari / K;
%  The number of iterations of the algorithm 
iter = eval_num / K;
w = 1;
%  Random generation 20 Data , And obtain its evaluation value 
sample_x = lhsdesign(num_initial, num_vari).*(upper_bound - lower_bound) + lower_bound.*ones(num_initial, num_vari);
sample_y = Rastrigin(sample_x);
Fmin = zeros(eval_num, 1);
aver_Fmin = zeros(eval_num, 1);

for n = 1 : 100
    n1 = 1;
    %  Initialize some parameters 
    pbestx = sample_x;
    pbesty = sample_y;
    %  Current location information presentx
    presentx = lhsdesign(num_initial, num_vari).*(upper_bound - lower_bound) + lower_bound.*ones(num_initial, num_vari);
    vx = sample_x;
    [fmin, gbest] = min(pbesty);
    global_best_x = pbestx(gbest, :);
    fprintf("n: %.4f\n", n);
    % fprintf("iter 0 fmin: %.4f\n", fmin);
    for i = 1 : iter
        for i1 = 1 : K
            ind = ((1 + (i1 - 1) * sub_num) : i1 * sub_num);
            r = rand(num_initial, sub_num);
            % pso Update the location of the next step , Here you can set the boundary if it exceeds the search range 
            vx(:, ind) = w.*vx(:, ind) + 2 * r .* (pbestx(:, ind) - presentx(:, ind)) + 2 * r .* (pbestx(gbest, ind) - presentx(:, ind));
            vx1 = vx(:, ind);
            vx1(vx1 > upper_bound) = upper_bound;
            vx1(vx1 < lower_bound) = lower_bound;
            vx(:, ind) = vx1;
            presentx(:, ind) = presentx(:, ind) + vx1;
            presentx1 = presentx(:, ind);
            presentx1(presentx1 > upper_bound) = upper_bound;
            presentx1(presentx1 < lower_bound) = lower_bound;
            presentx(:, ind) = presentx1;

            presentx2 = repmat(global_best_x, num_initial, 1);
            presentx2(:, ind) = presentx1;
            presenty = Rastrigin(presentx2);

            %  Update the best location for each individual 
            pbestx1 = pbestx(:, ind);
            pbestx1(presenty < pbesty, :) = presentx1(presenty < pbesty, :);
            pbestx(:, ind) = pbestx1;
            pbesty(presenty < pbesty, :) = presenty(presenty < pbesty, :);
            
            %  Update the best location of all individuals 
            [fmin, gbest] = min(pbesty);
            global_best_x = pbestx(gbest, :);
            Fmin(n1, 1) = fmin;
            n1 = n1 +1;
            % fprintf("iter %d fmin: %.4f\n", i, fmin);
        end
    end
    aver_Fmin = aver_Fmin + Fmin;
end
aver_Fmin = aver_Fmin ./ 100;
plot(aver_Fmin);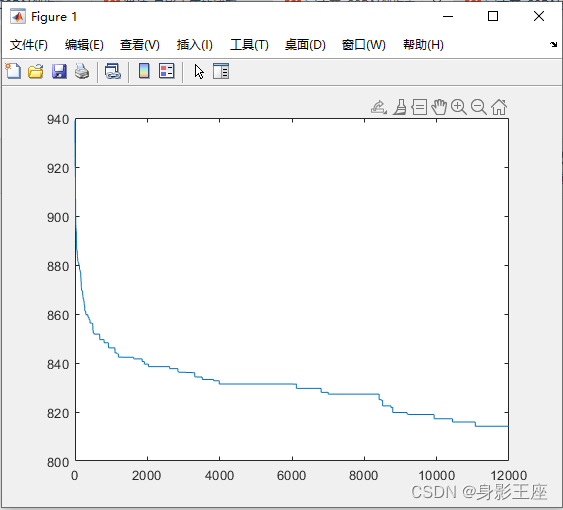

CPSO_Hk( Repeat the experiment 100 Time , Average. )： The evaluation times are about half less than the above two .

clc;clear;clearvars;
%  Random generation 20 Data ,P10 individual ,Q10 individual 
num_initial1 = 10;
num_initial2 = 10;
num_vari = 60;
%  Search range 
upper_bound = 5.12;
lower_bound = -5.12;
%  Calculate during iteration y Total number of values 
eval_num = 12000;
% K Represents the number of partitioned subspaces ,sub_num Represents the dimension of each subspace 
K = 6;
sub_num = num_vari / K;
%  The number of iterations of the algorithm 
iter = eval_num / K;
w = 1;
%  Random generation 10\10 Data , And obtain its evaluation value 
sample_x1 = lhsdesign(num_initial1, num_vari).*(upper_bound - lower_bound) + lower_bound.*ones(num_initial1, num_vari);
sample_y1 = Rastrigin(sample_x1);
sample_x2 = lhsdesign(num_initial2, num_vari).*(upper_bound - lower_bound) + lower_bound.*ones(num_initial2, num_vari);
sample_y2 = Rastrigin(sample_x2);
Fmin = zeros(iter, 1);
aver_Fmin = zeros(iter, 1);

for n = 1 : 100
    n1 = 1;
    %  Initialize some parameters 
    pbestx1 = sample_x1;
    pbesty1 = sample_y1;
    pbestxx = sample_x2;
    pbestyy = sample_y2;
    %  Current location information presentx
    presentx1 = lhsdesign(num_initial1, num_vari).*(upper_bound - lower_bound) + lower_bound.*ones(num_initial1, num_vari);
    presentxx = lhsdesign(num_initial2, num_vari).*(upper_bound - lower_bound) + lower_bound.*ones(num_initial2, num_vari);
    vx1 = sample_x1;
    vxx = sample_x2;
    [fmin1, gbest1] = min(pbesty1);
    [fmin2, gbest2] = min(pbestyy);
    global_best_x1 = pbestx1(gbest1, :);
    fprintf("n: %.4f\n", n);
    % fprintf("iter 0 fmin: %.4f\n", fmin);
    for i = 1 : iter
        for i1 = 1 : K
            ind = ((1 + (i1 - 1) * sub_num) : i1 * sub_num);
            r1 = rand(num_initial1, sub_num);
            % cpso Update the location of the next step , Here you can set the boundary if it exceeds the search range 
            vx1(:, ind) = w.*vx1(:, ind) + 2 * r1 .* (pbestx1(:, ind) - presentx1(:, ind)) + 2 * r1 .* (pbestx1(gbest1, ind) - presentx1(:, ind));
            vx2 = vx1(:, ind);
            vx2(vx2 > upper_bound) = upper_bound;
            vx2(vx2 < lower_bound) = lower_bound;
            vx1(:, ind) = vx2;
            presentx1(:, ind) = presentx1(:, ind) + vx2;
            presentx2 = presentx1(:, ind);
            presentx2(presentx2 > upper_bound) = upper_bound;
            presentx2(presentx2 < lower_bound) = lower_bound;
            presentx1(:, ind) = presentx2;

            presentx3 = repmat(global_best_x1, num_initial1, 1);
            presentx3(:, ind) = presentx2;
            presenty1 = Rastrigin(presentx3);

            %  Update the best location for each individual 
            pbestx2 = pbestx1(:, ind);
            pbestx2(presenty1 < pbesty1, :) = presentx2(presenty1 < pbesty1, :);
            pbestx1(:, ind) = pbestx2;
            pbesty1(presenty1 < pbesty1, :) = presenty1(presenty1 < pbesty1, :);
            
            %  Update the best location of all individuals 
            [fmin1, gbest1] = min(pbesty1);
            global_best_x1 = pbestx1(gbest1, :);
        end

        %  In this paper, the s/2 Namely num_initial2, The following is PSO Algorithm 
        ki = randi(num_initial2);
        while ki == gbest2
            ki = randi(num_initial2);
        end
        %  Information exchange 
        presentxx(ki, :) = global_best_x1;
        r2 = rand(num_initial2, num_vari);
        % pso Update the location of the next step , Here you can set the boundary if it exceeds the search range 
        vxx = w.*vxx + 2 * r2 .* (pbestxx - presentxx) + 2 * r2 .* (pbestxx(gbest2, :) - presentxx);
        vxx(vxx > upper_bound) = upper_bound;
        vxx(vxx < lower_bound) = lower_bound;
        presentxx = presentxx + vxx;
        presentxx(presentxx > upper_bound) = upper_bound;
        presentxx(presentxx < lower_bound) = lower_bound;
        presentyy = Rastrigin(presentxx);
        %  Update the best location for each individual 
        pbestxx(presentyy < pbestyy, :) = presentxx(presentyy < pbestyy, :);
        pbestyy(presentyy < pbestyy, :) = presentyy(presentyy < pbestyy, :);
        %  Update the best location of all individuals 
        [fmin2, gbest2] = min(pbestyy);
        %  Information exchange 
        for i2 = 1 : K
            kj = randi(num_initial1);
            while kj == gbest1
                kj = randi(num_initial1);
            end
            ind2 = ((1 + (i2 - 1) * sub_num) : i2 * sub_num);
            presentx1(kj, ind2) = pbestxx(gbest2, ind2);
        end

        % Get the global optimal value 
        if(fmin2 > fmin1)
            fmin = fmin1;
        else
            fmin = fmin2;
        end
        Fmin(n1, 1) = fmin;
        n1 = n1 +1;
        %fprintf("iter %d fmin: %.4f\n", i, fmin);
    end
    aver_Fmin = aver_Fmin + Fmin;
end
aver_Fmin = aver_Fmin ./ 100;
plot(aver_Fmin);

although CPSO_Sk and CPSO_Hk Compared with PSO Not much improvement , But its idea of delimiting molecular space is still very rare . In fact, with the improvement of the problem dimension ,CPSO_Sk and CPSO_Hk The running time of is less than PSO Of , Because the total operation is reduced . And from the end result CPSO_Hk Performance of >CPSO_Sk>PSO.

原网站

版权声明
本文为[Figure throne]所创，转载请带上原文链接，感谢
https://yzsam.com/2022/187/202207060119162576.html