当前位置:网站首页>AcWing 344. Solution to the problem of sightseeing tour (Floyd finding the minimum ring of undirected graph)
AcWing 344. Solution to the problem of sightseeing tour (Floyd finding the minimum ring of undirected graph)
2022-07-07 01:36:00 【Mr. Qiao Da】
AcWing 344. Sightseeing tour
Use this question floyd To find the minimum ring problem of undirected graphs , Pay attention to the sequence and significance of recording the path and finding the minimum intermediate point ( Because what is required is a ring , When you first find the ring , here k Not updated to i、j The shortest point between , So in path[cnt ++ ] = k And the next line get_min in path[cnt ++ ] = k Of k Values are different , It is guaranteed to be a ring )
#include<bits/stdc++.h>
using namespace std;
const int N = 110, INF = 0x3f3f3f3f;
int n, m;
int d[N][N], w[N][N]; //d Store the shortest path ,w Store edge weights
int path[N];
int pos[N][N];
int cnt;
void get_path(int i, int j){
if(pos[i][j] == 0) return ;
int k = pos[i][j];
get_path(i, k); // find i And the middle point k And save path Array
path[cnt ++ ] = k;
get_path(k, j); // find k and j And save path Array
}
signed main()
{
cin>>n>>m;
memset(w, 0x3f, sizeof w);
for(int i = 1; i <= n; i ++ ) w[i][i] = 0;
while(m -- ){
int a, b, c;
cin>>a>>b>>c;
w[a][b] = w[b][a] = min(w[a][b], c);
}
int res = INF;
memcpy(d, w, sizeof d);
for(int k = 1; k <= n; k ++ ){
// What is more puzzling here is why to seek the path first , Find the shortest distance between two points
// as a result of , here k Not updated to i、j The shortest point between
// So in path[cnt ++ ] = k And the next line get_min in path[cnt ++ ] = k Of k Values are different , It is guaranteed to be a ring
// Find the path first
for(int i = 1; i < k; i ++ ){
for(int j = i + 1; j < k; j ++ ){
if(res > (long long)d[i][j] + w[k][i] + w[j][k]){
// Find a smaller ring
res = d[i][j] + w[k][i] + w[j][k]; // Pay attention to the direction of the ring
cnt = 0; // Re record the path
path[cnt ++ ] = k; // This ring is from k set out
path[cnt ++ ] = i;
get_path(i, j);
path[cnt ++ ] = j;
}
}
}
// Find the middle point
for(int i = 1; i <= n; i ++ ){
for(int j = 1; j <= n; j ++ ){
if(d[i][j] > d[i][k] + d[k][j]){
d[i][j] = d[i][k] + d[k][j];
pos[i][j] = k;
}
}
}
}
if(res == INF) cout<<"No solution."<<endl;
else{
for(int i = 0; i < cnt; i ++ ) cout<<path[i]<<' ';
cout<<endl;
}
return 0;
}
边栏推荐
- uva 1401 dp+Trie
- POJ 3177 Redundant Paths POJ 3352 Road Construction(双连接)
- json学习初体验–第三者jar包实现bean、List、map创json格式
- 字节P7专业级讲解:接口测试常用工具及测试方法,福利文
- Byte P7 professional level explanation: common tools and test methods for interface testing, Freeman
- 搭建【Redis in CentOS7.x】
- 安利一波C2工具
- 2022 Google CTF SEGFAULT LABYRINTH wp
- Yunna | work order management software, work order management software app
- Sword finger offer II 035 Minimum time difference - quick sort plus data conversion
猜你喜欢
Let's see how to realize BP neural network in Matlab toolbox
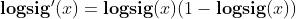
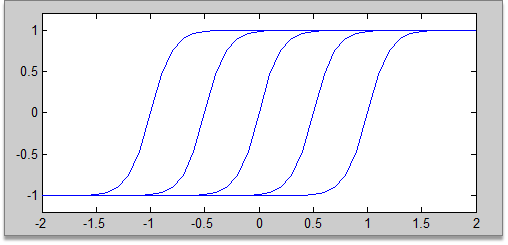
The difference between Tansig and logsig. Why does BP like to use Tansig
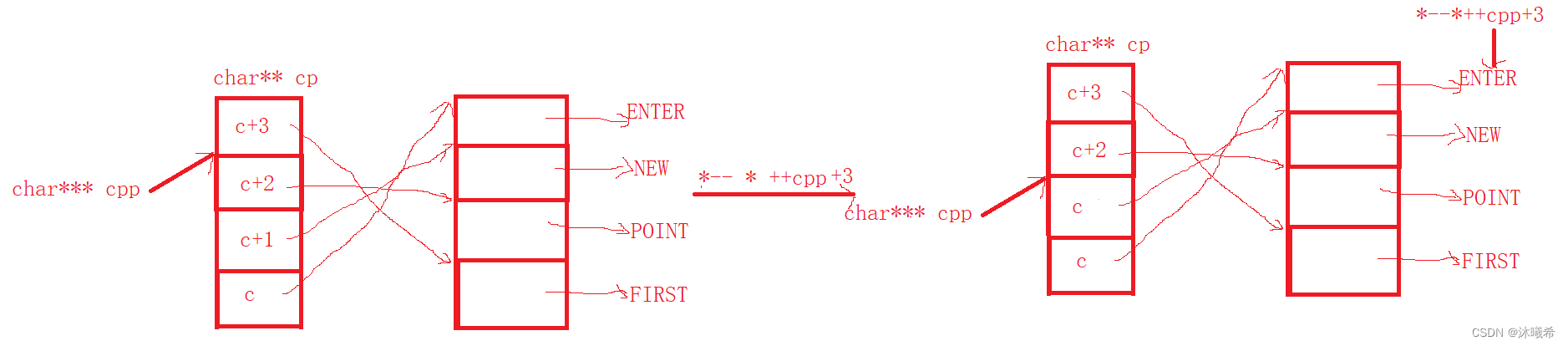
【C语言进阶篇】指针的8道笔试题

ClickHouse字段分组聚合、按照任意时间段粒度查询SQL
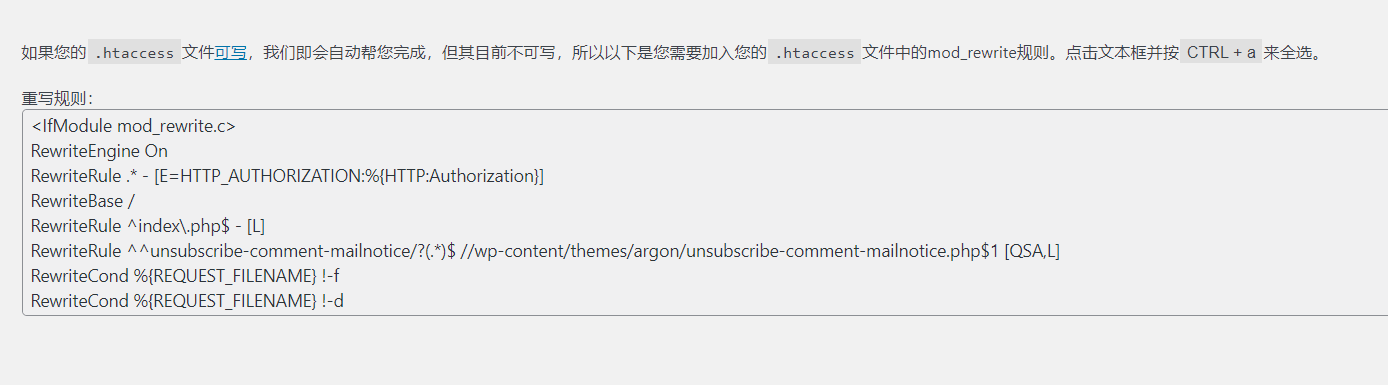
设置Wordpress伪静态连接(无宝塔)

鼠标右键 自定义
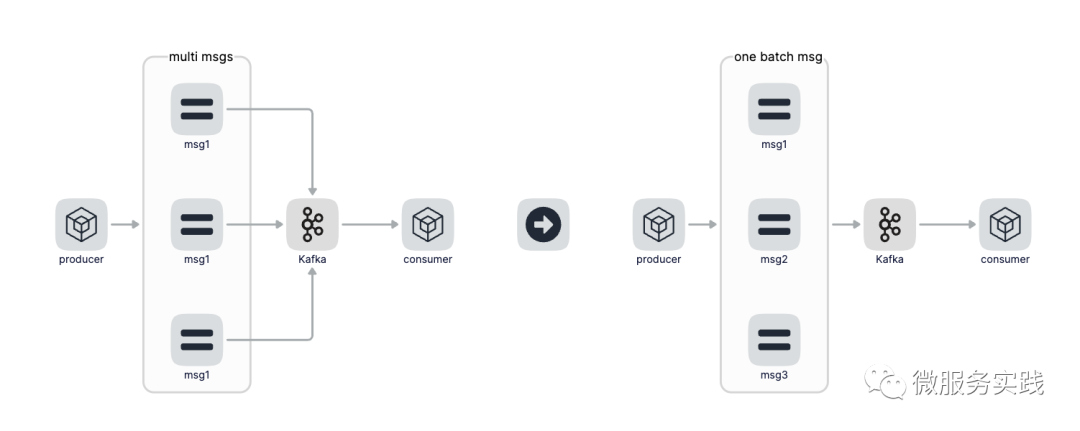
go-zero微服务实战系列(九、极致优化秒杀性能)
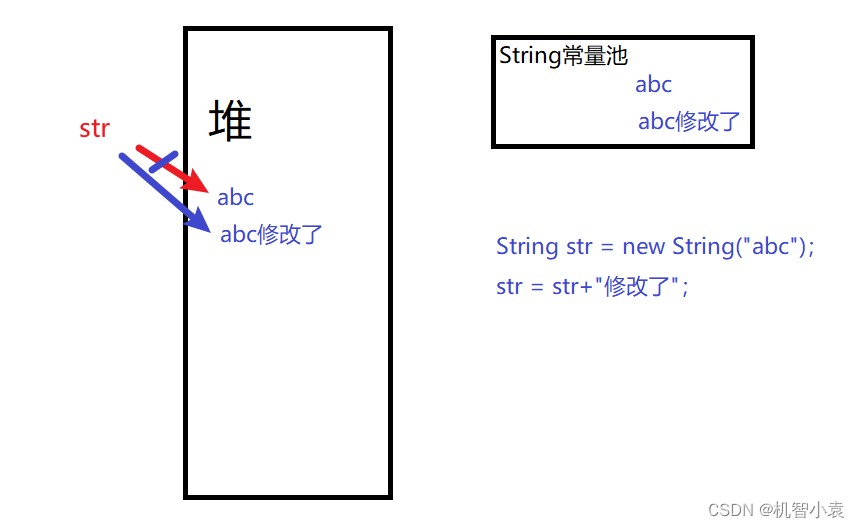
Today's question -2022/7/4 modify string reference type variables in lambda body
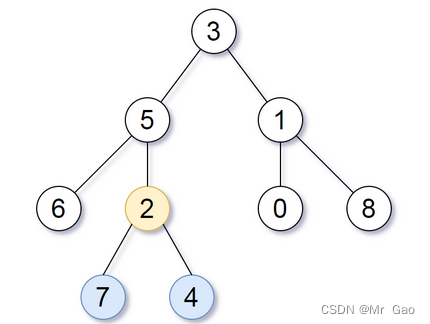
1123. The nearest common ancestor of the deepest leaf node

今日问题-2022/7/4 lambda体中修改String引用类型变量
随机推荐
公钥\私人 ssh避password登陆
安利一波C2工具
Make Jar, Not War
THREE.AxesHelper is not a constructor
C language instance_ three
curl 命令
使用nodejs完成判断哪些项目打包+发版
Appium自动化测试基础 — uiautomatorviewer定位工具
docker 方法安装mysql
[signal and system]
Metauniverse urban legend 02: metaphor of the number one player
免费白嫖的图床对比
Taro2.* applet configuration sharing wechat circle of friends
C language - array
Installation of gazebo & connection with ROS
POJ 3177 Redundant Paths POJ 3352 Road Construction(双连接)
【C语言进阶篇】指针的8道笔试题
LeetCode:1175. 质数排列
What does front-end processor mean? What is the main function? What is the difference with fortress machine?
C语言实例_4