当前位置：网站首页>Reinforcement learning - learning notes 8 | Q-learning

Reinforcement learning - learning notes 8 | Q-learning

2022-07-07 18:36:00 【climerecho】

I got to know you in the last note Sarsa, It can be used to train the action value function $Q_\pi$; Learn this article Q-Learning, This is another kind of TD Algorithm , For learning Optimal action value function Q-star, This is used for training in previous value learning DQN The algorithm of .

8. Q-learning

Continue the doubts of the previous article , Compare the two algorithms .

8.1 Sarsa VS Q-Learning

These are both TD Algorithm , But the problems solved are different .

Sarsa

Sarsa Training action value function $Q_\pi(s,a)$;
TD target：$y_t = r_t + \gamma \cdot {Q_\pi(s_{t+1},a_{t+1})}$
The value network is $Q_\pi$ Functional approximation of ,Actor-Critic Method in , use Sarsa Update the value network (Critic)

Q-Learning

Q-learning It is the value function of training the best action $Q^*(s,a)$
TD target :$y_t = r_t + \gamma \cdot {\mathop{max}\limits_{a}Q^*(s_{t+1},a_{t+1})}$, Yes Q Maximize
Note that this is the difference .
use Q-learning Training DQN

The difference between personal summary is Sarsa Actions are sampled randomly , and Q-learning Is to take the expected maximum

Here's the derivation Q-Learning Algorithm .

8.2 Derive TD target

Be careful Q-learning and Sarsa Of TD target There's a difference .

Before Sarsa This equation is proved ：$Q_\pi({s_t},{a_t})=\mathbb{E}[{R_t} + \gamma \cdot Q_\pi({S_{t+1}},{A_{t+1}})]$

Equation means ,$Q_\pi$ It can be written. Reward as well as $Q_\pi$ An estimate of the next moment ;
Both ends of the equation have Q, And for all $\pi$ All set up .

So record the optimal strategy as $\pi^*$, The above formula is also true , Yes ：

$Q_{\pi^*}({s_t},{a_t}) = \mathbb{E}[{R_t} + \gamma \cdot Q_{\pi^*}({S_{t+1}},{A_{t+1}})]$

Usually put $Q_{\pi^*}$ Write it down as $Q^*$, Can represent the optimal action value function , So you get ：

$Q^*({s_t},{a_t})=\mathbb{E}[{R_t} + \gamma \cdot Q^*({S_{t+1}},{A_{t+1}})]$

Handle the right side Expected $Q^*$, Write it in maximized form ：

because $A_{t+1} = \mathop{argmax}\limits_{a} Q^*({S_{t+1}},{a})$ ,A It must be maximization $Q^*$ The action of
explain ：
Given state $S_{t+1}$,Q* Will score all actions ,agent Will perform the action with the highest score .
therefore $Q^*({S_{t+1}},{A_{t+1}}) = \mathop{max}\limits_{a} Q^*({S_{t+1}},{a})$,$A_{t+1}$ Is the best action , Can be maximized $Q^*$;
Bring in the expectation to get ：$Q^({s_t},{a_t})=\mathbb{E}[{R_t} + \gamma \cdot \mathop{max}\limits_{a} Q^*({S_{t+1}},{a})]$
On the left is t Prediction of time , Equal to the expectation on the right , Expect to maximize ; It's hard to expect , Monte Carlo approximation . use $r_t \ s_{t+1}$ Instead of $R_t \ S_{t+1}$;
Do Monte Carlo approximation ：$\approx {r_t} + \gamma \cdot \mathop{max}\limits_{a} Q^*({s_{t+1}},{a})$ be called TD target $y_t$.
here $y_t$ There are some real observations , So it's better than the left Q-star A complete guess should be reliable , So try to make the left side Q-star near $y_t$.

8.3 The algorithm process

a. Form

observation One transition$({s_t},{a_t},{r_t},{s_{t+1}})$
use $s_{t+1} \ r_t$ Calculation TD target：${r_t} + \gamma \cdot \mathop{max}\limits_{a} Q^*({s_{t+1}},{a})$
Q-star This is a table like the following figure ：

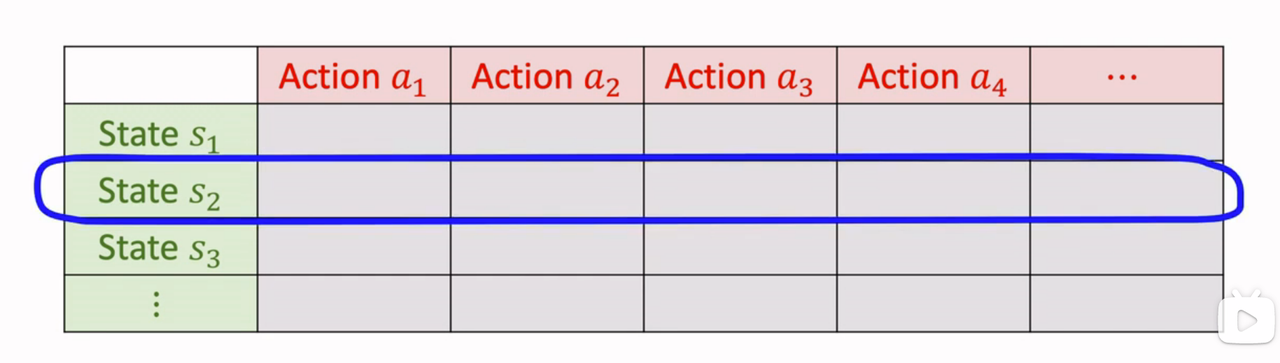
Find the status $s_{t+1}$ Corresponding That's ok , Find the biggest element , Namely $Q^*$ About a The maximum of .

Calculation TD error: $\delta_t = Q^*({s_t},{a_t}) - y_t$
to update $Q^*({s_t},{a_t}) \leftarrow Q^*({s_t},{a_t}) - \alpha \cdot \delta_t$, to update $(s_{t},a_t)$ Location , Give Way Q-star It's closer to $y_t$

b. DQN form

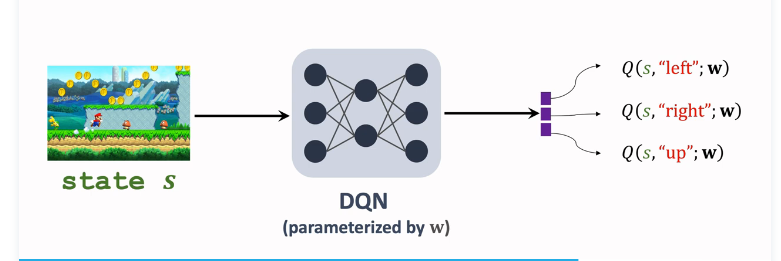
DQN $Q^*({s},{a};w)$ The approximate $Q^*({s},{a}) $, The input is the current state s, Output is the scoring of all actions ;

Next, choose the action of maximizing value ${a_t}= \mathop{argmax}\limits_{{a}} Q^*({S_{t+1}},{a},w)$, Give Way agent perform $a_t$; Use the collected transitions Learn training parameters w, Give Way DQN Of q More accurate ;

use Q-learning Training DQN The process of ：
Observe a transition $({s_t},{a_t},{r_t},{s_{t+1}})$
TD target: ${r_t} + \gamma \cdot \mathop{max}\limits_{a} Q^*({s_{t+1}},{a};w)$
TD error: $\delta_t = Q^*({s_t},{a_t};w) - y_t$
gradient descent , Update parameters : $w \leftarrow w -\alpha \cdot \delta_t \cdot \frac{{s_t},{a_t};w}{\partial w}$