当前位置:网站首页>[paper sharing] where's crypto?
[paper sharing] where's crypto?
2022-07-07 18:21:00 【fa1c4】
Where’s Crypto?: Automated Identification and Classification of Proprietary Cryptographic Primitives in Binary Code [USENIX 2021]
Carlo Meijer Radboud University The Netherlands [email protected]
Veelasha Moonsamy Ruhr University Bochum Germany [email protected]
Jos Wetzels Midnight Blue Labs The Netherlands [email protected]
summary
Proprietary cryptographic technology will be used in embedded systems in many industries , From physical access control systems and Telecommunications (telecommunications) To the machine - Machine authentication , All pose a major obstacle to the black box safety assessment . In depth security analysis is usually required in a large number of binary Location and classification algorithm in code , Even with the help of heuristics, manual inspection , It's also time-consuming .
This paper presents an automatic recognition and classification in binary code ( proper ) A new method of cryptographic primitives . The method is based on data flow graph (Data Flow Graph, DFG) isomorphism , Previously by Lestringant wait forsomeone [43] Put forward . But their DFG Isomorphic methods are limited to known primitives , And it depends on the heuristic method of selecting code fragments for analysis . By combining the above method with symbolic execution , Overcome [43] The limitation of , And can extend the analysis to unknown 、 Proprietary cryptographic primitive field .
In order to prove that the thesis scheme is feasible , The author developed various signatures , Each signature is for a different encryption primitive class , The experimental evaluation of each signature is carried out on a set of binary files , These binaries include publicly available ( These provide reproducible results ) And proprietary binaries . Last , The author uses IDA An open source implementation has been released in the form of disassembly plug-ins , be known as “Where’s Crypto?”.
In a word : combination DFG Isomorphism and symbols perform the identification and classification of cryptographic primitives in binary files .
Thesis link :https://www.usenix.org/conference/usenixsecurity21/presentation/meijer
github Address :https://github.com/wheres-crypto/wheres-crypto
Introduction
Although academia generally believes that cryptography should be publicly recorded , However, the use of private cryptography persists in many industry verticals , From physical access control systems and telecommunications to machine to machine authentication . This situation is important for certification 、 Compliance check 、 Safety assessment or personal research work constitutes a major obstacle , Because it needs to resort to highly labor-intensive Reverse Engineering , In order to determine the existence and nature of these algorithms before evaluation . Besides , When a specific algorithm is broken , Due to confidentiality agreement or court injunction , Details may not be released immediately , This makes other potential affected parties repeat this expensive effort , And hinders effective vulnerability management . therefore , What is really needed is a practical solution , Automatically scan binaries , To discover unknown cryptographic algorithms .
standard
( It's also a contribution , The previous work has not met the requirements of this standard
(i) Identify unknown encryption algorithms of related types
(ii) Efficiently support large real embedded binary firmware
(iii) Do not rely on complete firmware simulation or dynamic instrumentation
contribution
(1 The first work performed by combining subgraph isomorphism and notation , It solves the open problem of code segment selection , Eliminates the need for heuristics , Thus, it overcomes the limitation that the previous work is not suitable for identifying unknown passwords , In addition, there is no work in industry or academia to solve the problem of identifying unknown cryptographic algorithms
(2 A new domain specific language is proposed (domain-specific language, DSL) To define the structural properties of cryptographic primitives
(3 Provide open source implementation , And evaluate according to the analysis time and the accuracy of binary files related to the real world
prior work
The previous work on binary password recognition in academia and industry can be divided into
(1 Special function identification is the simplest 、 The most direct way is to OS api Special password function of formal identification
( Such as Windows CryptoAPI/CNG), Library import or special instructions ( Such as AES-NI). This method is inherently unable to detect unknown algorithms .
(2 The most commonly used methods in practice include constant based ( for example IVs, Sleeveless numbers , fill ) And lookup tables ( Such as S-Boxes, P-Boxes). This method is not suitable for the detection of unknown algorithms . Besides , This also applies to known algorithms that do not rely on fixed data , Or algorithms that rely on fixed data , for example , Use dynamically generated s - box, Not embedded s - box.
(3 Code heuristics : They can be applied statically or dynamically , For example, mnemonic constant tuples , It takes into account the size of words 、 Byte order 、 Multiplication and the inverse of addition , But it has the same shortcomings as data signature in other aspects . The second heuristic relies on the observation that symmetric cryptographic routines tend to consist of a high proportion of bit arithmetic instructions , And try to classify the function according to the threshold .
(4 Deep learning : A method based on dynamic convolution neural network is proposed , However , Because it relies on dynamic binary instruments , It cannot classify unknown algorithms .
(5 Data flow analysis : Depends on the static relationship between the function and its input and output . One possible approach is to perform a stain analysis and evaluation function I/O Entropy change , This depends on simulation , For the standard of this paper (iii) This is not appropriate . Another method is to simulate or symbolic functions I/O Compare with the set of reference implementation or test vectors , This is essentially unable to detect unknown algorithms .
programme
hypothesis
(1 Try to build semantic equivalence classes and DFGs The one-to-one mapping between is beyond the scope of this work . When normalization maps two expressions to the same DFG Node time , Suppose they are semantically equivalent . Although the reverse is not necessarily true .
(2 Because code obfuscation is an inherent challenge to any binary analysis method , Our method assumes that the inputs it operates on are not confused , And delegate this disambiguation to manual and / Or automatic preprocessing steps .
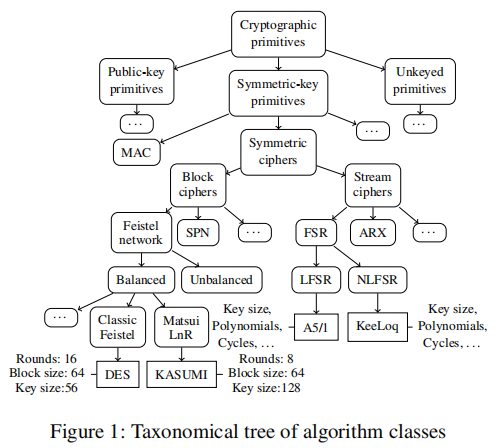
(3 PoC Evaluate and DSL Example , The author will limit the discussion to a subset of the classification of cryptographic primitives . This is not an inherent limitation of the thesis method , And just give PoC And the limitations of its evaluation . The method of the paper is basically independent of the classification used , It can be extended according to the needs of users , And just assume that the algorithm the analyst is looking for is in one of its classes . Since the vast majority of proprietary cryptography belongs to the established primitive class [67] A specific subset of , Stream cipher, block cipher and hash function , The author doesn't think this is a problem .
(4 False positives : Some primitive classes are subsets of other classes , Some instances conform to the definition of several classes , Thus, false positives of classification may occur . Suppose the tool is only used to assist manual reverse , Do not consider the impact of false positives , Because it is easy to prune the false alarm manually .
Password primitive
The method is based on the structural classification of encryption primitives . The author's idea is , Because the vast majority of proprietary cryptography belongs to the established basic classes [67], You can develop structural signatures , Allow any algorithm to be identified in these classes , Instead of relying on special knowledge of the algorithm .
The overall method is based on two foundations : Data flow diagram (DFG) Isomorphism and symbolic execution . The advantage of this method is that the enhancement effect implemented by symbols breaks through the original simple use DFG Isomorphism is the limitation of cryptographic primitive recognition , It makes it more advantageous to locate the structure signature and analyze the binary code to find the match of cryptographic primitives .
This thesis mainly studies symmetric ciphers and keyless primitives (unkeyed primitives)
Encryption primitives are essentially a set of representations of inputs / Arithmetic and logical operations of output relations . This structural relationship between data and operations can be expressed as DFG. Generally speaking, the structure of a specific algorithm will be similar to that of a general cryptographic primitive , Then identifying which cryptographic basic class an unknown algorithm belongs to can be attributed to DFG Subgraph isomorphism of .
However , Due to subtle differences in implementation and compiler features , Algorithms with the same semantics DFG Indicates that it may be different , Before isomorphic analysis , This representation needs to be normalized . Interestingly, there has been a conclusion in theory , Lestringant wait forsomeone [43] prove , Through to DFG Apply a set of rewrite rules repeatedly , You can get a standardized version , Many of these changes have been deleted . Although there is no guarantee that equivalent semantics will always map to the same DFG, But the result “ Good enough. ”, It can be used as a data structure for this purpose .
DFG
Suppose there is an assembly instruction sequence , Then convert each instruction into a set of operations O i O_i Oi, It can be an empty set or a set with multiple operations . Then distinguish the type of each input
(1) Count now : Create a vertex , representative G A constant value in . It passes through an edge with O i O_i Oi Connected to a .
(2) register : If the instruction takes the register as the input operand , Then write the value of this register and O i O_i Oi Create an edge between
(3) Memory : For operands loaded or stored from memory , establish load and store operation . Both operations take the memory address vertex as input .
The paper [43] The method followed is to use generated DFG, And repeatedly apply standardized rewrite rules , Until the fixed point is reached . This is the difference between the method in this article and their method , Although this article also applies standardization , But it will be applied continuously in the process of graph construction . This improves performance , And allows efficient tracking of conditions applied during symbol execution .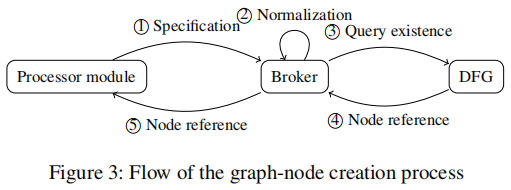
There is a processor module , It is written for a specific architecture , Convert each instruction into a graph node . The processor module cannot create new graph nodes by itself . contrary , It must interact with the agent . The proxy is responsible for normalizing the application of rewrite rules , And it has nothing to do with the processor architecture . The processor module provides the proxy with the specifications of the required nodes , The proxy applies the canonical rewrite rule to the specification . therefore , The result either exactly matches the specification , Or match with different specifications that are semantically equivalent . After normalization , Agent to DFG Query whether the node that conforms to the normalization specification already exists . If it is , Then return a reference to it , Instead of creating a new node . therefore , It is impossible for two different nodes in a graph to conform to the same specification , Or equivalent under standardization .
Normalize rewrite rules : Including operation simplification 、 Common subexpression elimination and subsequent (subsequent) Memory access for .
The operation is simplified Suppose we encounter an arithmetic / Logical operations , All input parameters are constants . then , This operation can be replaced by its result .
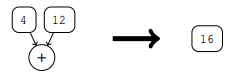
Common subexpression Elimination is usually in a code fragment , The same value will be recalculated several times .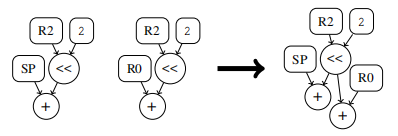
Memory access Loading and storing data from main memory is a common operation . However , It doesn't have to be semantic , But it may be due to register filling and overflow .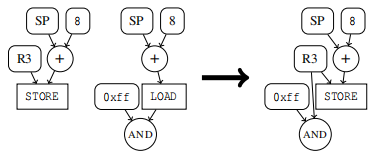
Advantages
There are several advantages of applying normalized rewriting rules in the construction of graphs over doing so after the graph is completely generated . First , If the normalization function h h h The running time complexity of is constant , Then the running time complexity of the construction phase including normalization increases linearly with the number of assembly instructions , And in a completely generated DFG The upper repeated application is the quadratic element complexity .
Purging and Subgraph isomorphism
constructed DFG After that, we'll have purging, This part is mainly about DFG Further simplification of , For details, please refer to the paper , Skip here . Then simplified DFG As input, execute the subgraph isomorphism search algorithm . Search subgraph isomorphism is NPC problem , Ullmann[66] The proposed solution is a recursive backtracking algorithm with pruning . This paper adopts UIImann Algorithm for isomorphic subgraph search .
Symbolic execution
In analyzing functions , We may encounter conditional instructions . For certain conditions , Input variables are restricted to one field , So there is only one possible evaluation result . such as , Conditional jump instruction at the end of a loop consisting of a fixed number of iterations . contrary , For uncertain conditions , Input variables are not limited enough to determine a fixed result .
In constructing any function f f f Of DFG In the process , Hold state S = ( G , P , B ) S = (G,P,B) S=(G,P,B), among G = ( V , E ) G = (V,E) G=(V,E) Partially constructed DFG. P P P Is the path condition , Construct during symbol execution ; Predicates that restrict unknown variables to a domain , such , If the conditions are met , The execution path will follow DFG The same path used during construction . let me put it another way : P P P Satisfaction guarantee G G G representative f f f The input of / The output relationship . The opposite is not necessarily true .
For uncertain conditional branches , The simple idea is that for every possible Branch fork Give an example and continue to execute downward , The result is one DFGs Set , Every DFG Represents a possible execution path , But this method will encounter the problem of state explosion , So it's not practical . Then the paper proposes a method to balance coverage and performance :
When to apply bifurcation strategy has little to do with symbol execution itself . therefore , We introduce the path Oracle, An independent entity queried in the graph construction stage , Every time an under determined condition occurs c. It decided c Is the calculation result of true or false , Or construct forks and follow two execution paths .
Path Oracle Policy
set up B It's a record. oracle Log of decisions made on the path .
Definition d e , i ∈ { T A K E _ T R U E , T A K E _ F A L S E , T A K E _ B O T H } d_{e,i} ∈ \{TAKE\_TRUE,TAKE\_FALSE,TAKE\_BOTH\} de,i∈{ TAKE_TRUE,TAKE_FALSE,TAKE_BOTH}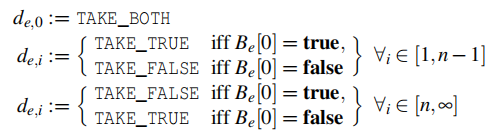
Simply speaking , If the execution path is selected to the branch where the password primitive is located , So in i = 0 The execution path at will allow us to revisit e. Our goal is to construct a primitive n Iterations consist of DFG, We repeat this path selection n - 1 Time , Then take the opposite path , Cause the execution flow to exit the loop . Last , The construction phase produces two DFG: A said 0 Sub iteration , Another way of saying n Sub iteration .
Signature Expression
To detect subgraph isomorphism , We need a way to represent the signature graph . chart 4 Describes the signature domain specific language (DSL) Schematic diagram . A circle indicates a keyword , The box represents the data type . Generate new graph nodes through expression data types .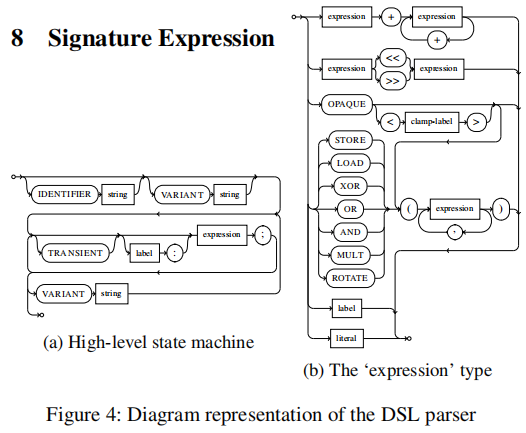
such as , LFSR Algorithm DFG by 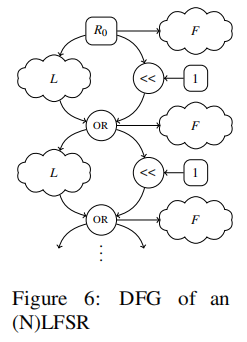
LFSR The signature of is 
Finally, the generated signature graph also needs to be normalized and purging And again DFG Isomorphic matching .
The paper defines a signature for each specific cryptographic algorithm , Specifically, it abstracts the properties of each cryptographic primitive into a DFG, Finally, it is transformed into DSL To accurately describe .
( The specific transformation process is the specific analysis of specific algorithms , The paper does not give a clear description of pseudocode .
experiment
Experimental index
Accuracy and running time
Graph construction
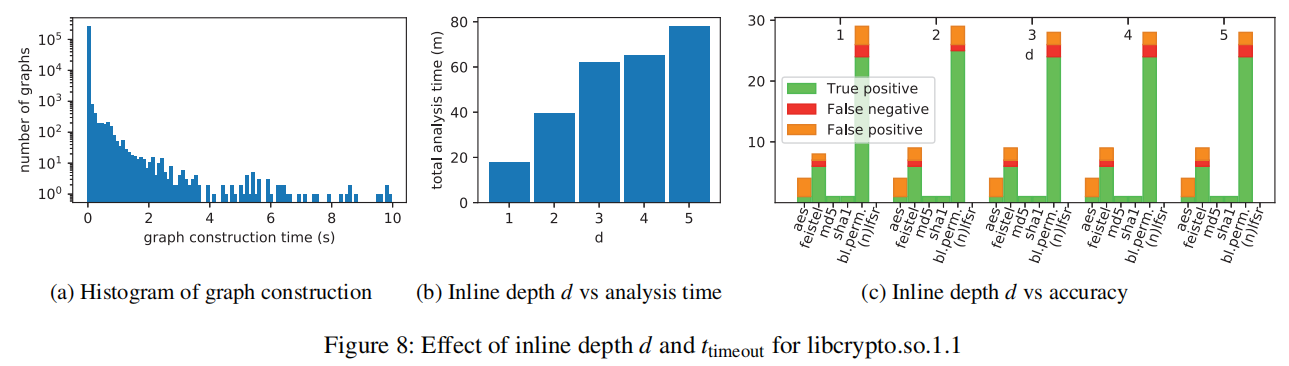
DFG Construction is affected by downtime , Therefore, there is no guarantee that the graphic construction will terminate . therefore , We introduce a graph construction timeout t t i m e o u t t_{timeout} ttimeout chart 8a It describes libcrypto.so.1.1 Graph construction time of all graphs constructed during analysis t Histogram .
It shows , For most graphs , Builds on the 10 seconds . So you can take t t i m e o u t t_{timeout} ttimeout = 10s.
Besides , We must decide what action to take when the analyzed function calls another function . We can either execute inline , Thus, the whole call is merged into the generated DFG in , Or through a single CALL Operation means it . To solve this problem , We define an adjustable variable d, Indicates the depth level to which the function call is inlined . By means of libcrypto.so.1.1 Run analysis on d Influence , Use different values at the same time , And measure performance in terms of running time and accuracy . chart 8b It is described in the d Under the influence of , complete libcrypto.so.1.1 The time spent in the whole analysis of each function in .
chart 8c Include the accuracy measurements for each signature . Omit the real negation , Because they cover most of the results , Therefore, readability is affected .
Password recognition
stay OpenWRT Is a commonly used network library , The corresponding binary file contains common password primitives .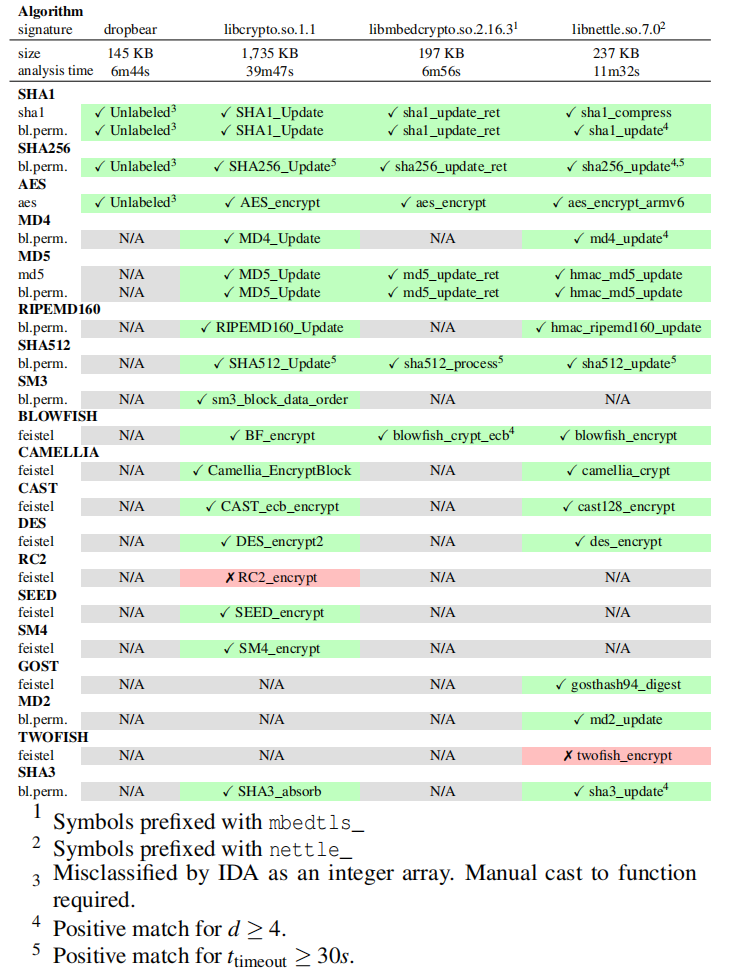
Each unit in the table describes the symbol name in the binary corresponding to the first positive result , perhaps , In case of false negative , A symbolic name that describes the expected positive result . It turns out that , The solution of this paper can successfully identify most of the cryptographic primitives in various binary files in time . If accuracy takes precedence over performance , You can tune parameters to improve detection .
summary
related work
[43] Pierre Lestringant, Frédéric Guihéry, and Pierre-Alain Fouque. Automated identification of cryptographic primitives in binary code with data flow graph isomorphism. In Proceedings of the 10th ACM Symposium on Information, Computer and Communications Security, pages 203–214. ACM, 2015.
[66] Julian R Ullmann. An algorithm for subgraph isomorphism. Journal of the ACM (JACM), 23(1):31–42, 1976.
[67] Roel Verdult. The (in) security of proprietary cryptography. PhD thesis, [Sl: sn], 2015.
Insights
(1) The existing methods of identifying cryptographic algorithms are not combined with symbol execution , Introduce symbolic execution and structural description of cryptographic primitives , Can get better results
(2) Refer to DSL describe , Similar processing can be carried out on the target in the binary file to assist the identification process
(3) Use comprehensive , Optimize , Semantic equivalence do binary code to confuse
边栏推荐
- 同消费互联网的较为短暂的产业链不同,产业互联网的产业链是相当漫长的
- 手撕Nacos源码(先撕客户端源码)
- [论文分享] Where’s Crypto?
- Use seven methods to enhance all the images in a folder
- 『HarmonyOS』DevEco的下载安装与开发环境搭建
- 备份阿里云实例-oss-browser
- Yarn capacity scheduler (ultra detailed interpretation)
- Five network IO models
- What are the financial products in 2022? What are suitable for beginners?
- 海量数据去重的hash,bitmap与布隆过滤器Bloom Filter
猜你喜欢
Introduction to OTA technology of Internet of things
How to clean when win11 C disk is full? Win11 method of cleaning C disk

Deep learning - make your own dataset
4种常见的缓存模式,你都知道吗?
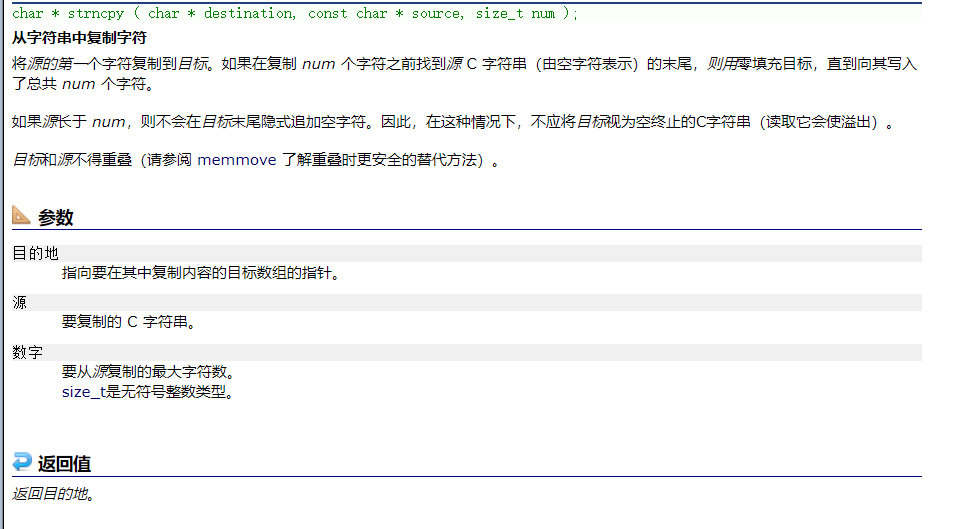
【C语言】字符串函数
Chapter 2 build CRM project development environment (database design)

A few simple steps to teach you how to see the K-line diagram

通过 Play Integrity API 的 nonce 字段提高应用安全性
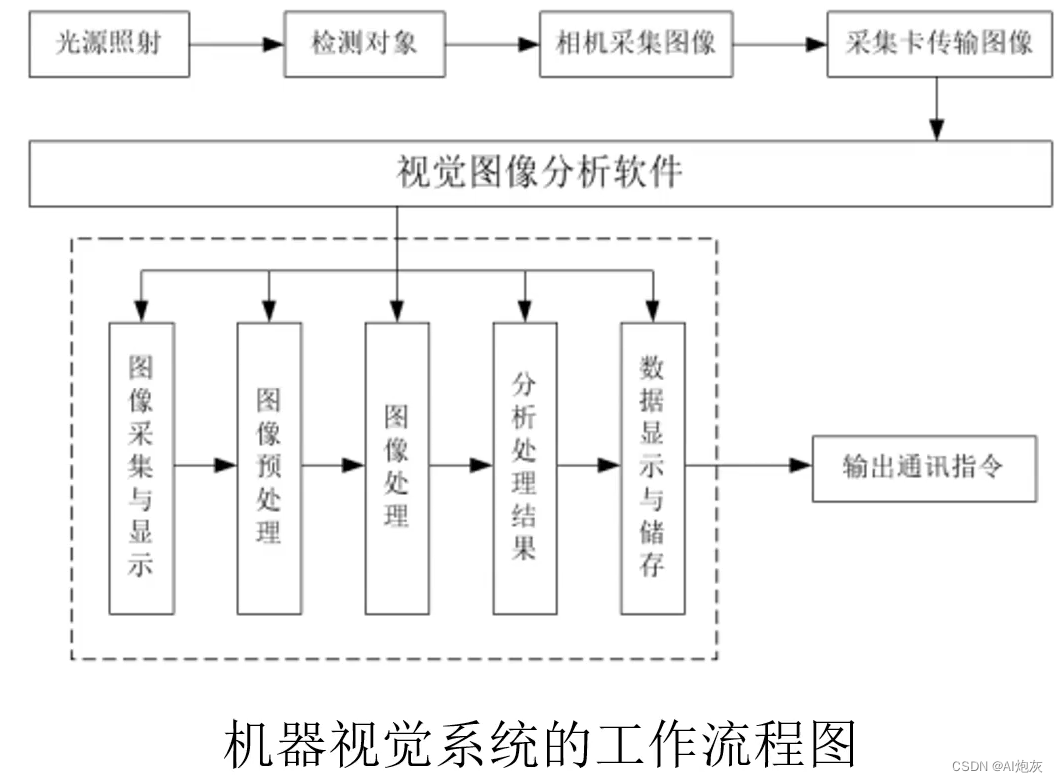
Machine vision (1) - Overview
科学家首次观察到“电子漩涡” 有助于设计出更高效的电子产品
随机推荐
Discuss | frankly, why is it difficult to implement industrial AR applications?
debian10系统问题总结
List selection JS effect with animation
More than 10000 units were offline within ten days of listing, and the strength of Auchan Z6 products was highly praised
nest.js入门之 database
Some key points in the analysis of spot Silver
[PaddleSeg源码阅读] PaddleSeg Validation 中添加 Boundary IoU的计算(1)——val.py文件细节提示
Discuss | what preparations should be made before ar application is launched?
zdog. JS rocket turn animation JS special effects
Chapter 3 business function development (user login)
In depth understanding of USB communication protocol
Nunjuks template engine
Main work of digital transformation
现货白银分析中的一些要点
Use seven methods to enhance all the images in a folder
Debian10 compile and install MySQL
[tpm2.0 principle and Application guide] Chapter 5, 7 and 8
Mui side navigation anchor positioning JS special effect
Five network IO models
Tips of the week 136: unordered containers