4、 Fundamentals of machine learning

1、 Training set (training), Cross validation set (dev) And test set (test)

\qquad After getting the raw data , The data needs to be divided into three parts ： Training set , Cross validation set test set . among , When the amount of data is small , May adopt 60/20/20 In proportion to ; When the amount of data is large , You can reduce the proportion of cross validation set and test set , If you use 98/1/1 To distribute . It is necessary to ensure that the distribution law of cross validation set and test set is the same as that of training set .

2、 deviation (bias) And variance (variance) To deal with

\qquad When you can't visualize by drawing images bias and variance when , We can judge whether the model is over fitting or under fitting by training set and deviation rate and cross validation set and deviation rate , The judgment method is as follows ：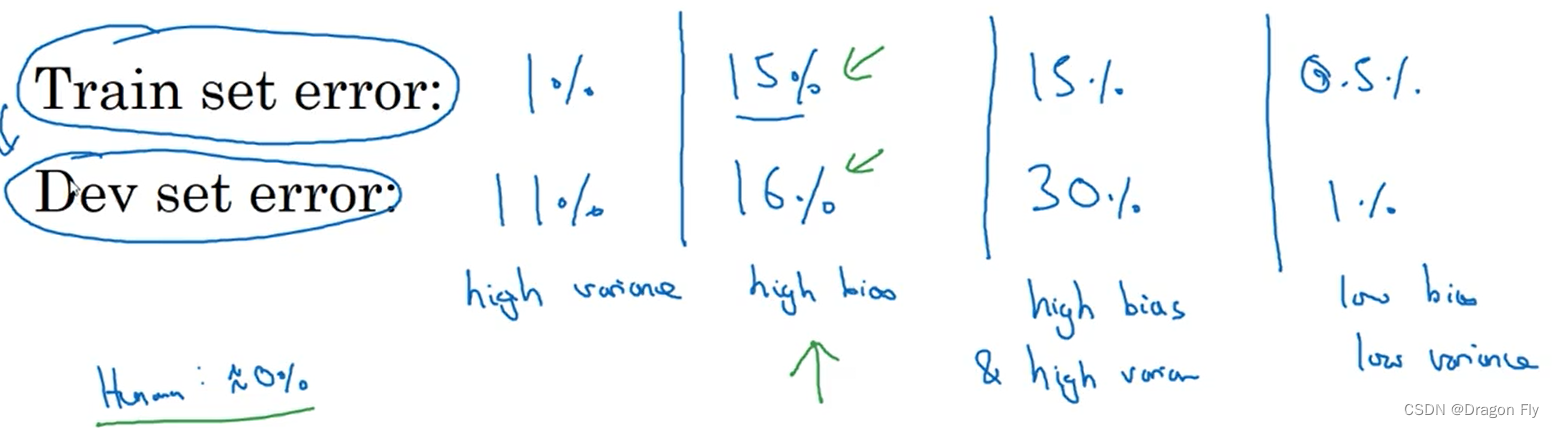

3、Basic recipe for machine learning

\qquad When designing a neural network model , First you can go through bias Values and variance Value to quickly judge whether the network design is reasonable , When higher bias when , You can deepen the number of layers of the network , Train more times to improve the network , until bias Relatively small until ; Then judge the current variance Is it also relatively small , If it appears variance In the larger case , You can get more data by , Normalization is used to improve the model . Then judge bias, So circular , Until bias and variance Are relatively small .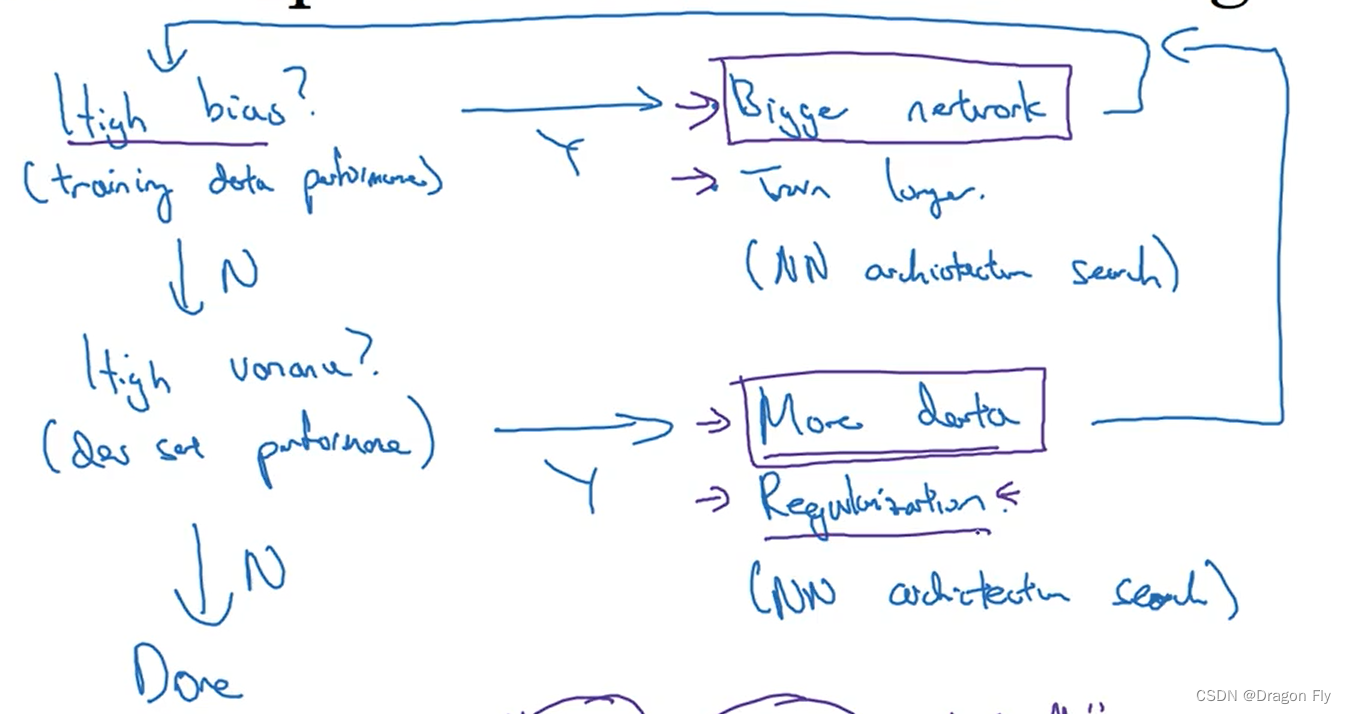

4、 Normalization of neural network / Regularization

\qquad When training neural networks, there is a phenomenon of over fitting , The first method that should be tried is normalization (regularization). Here's an example , The regularization of the logistic regression problem is as follows ：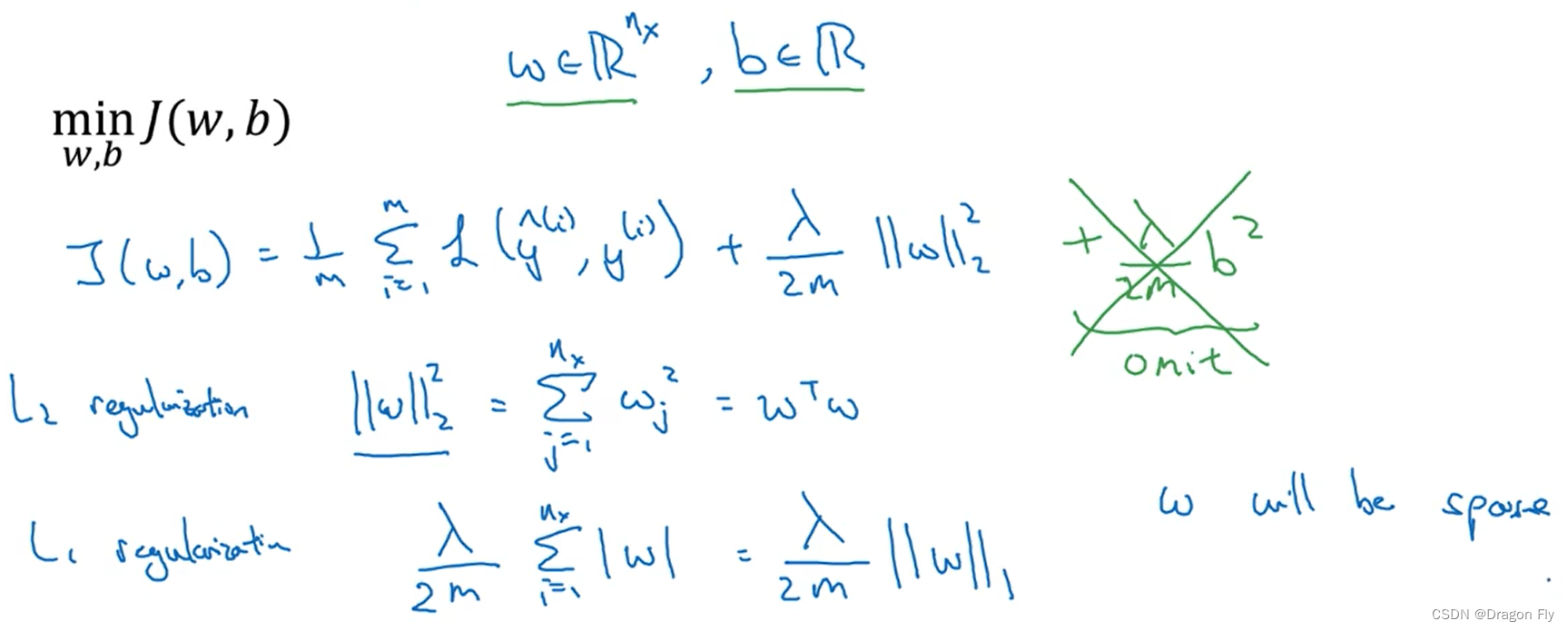

\qquad Use $L_2$ After regularization , In back propagation , Update parameters W When , There will be a coefficient reduction , bring W The value of is smaller than when regularization is not used , It's called weight decay. After the regularization item is added $d{w}^{[l]}=(frombackprop)+\frac{\lambda }{m}{w}^{[l]}$,recall The parameter update rule is ：$w^{[l]}=w^{[l]}-\alpha (d{w}^{[l]})$, Can be launched $w^{[l]}=w^{[l]}-\frac{\alpha \lambda }{m}{w}^{[l]}-\alpha (frombackprop)$

4.1 The reason why regularization can reduce the risk of over fitting

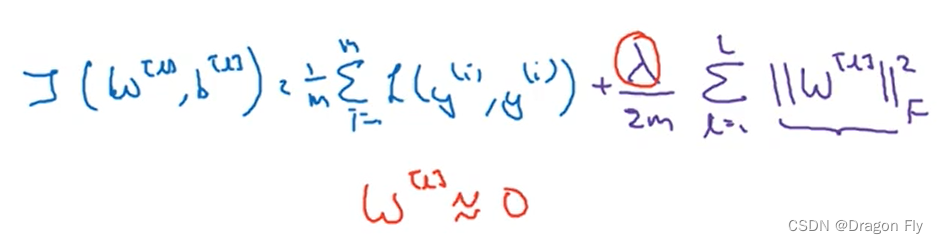
\qquad First, understand intuitively , When regularization parameters $\lambda$ When the setting is large , Weight item $W$ Will be reduced accordingly , Because the goal is to minimize the loss function $J$, It can be approximately understood as reducing the influence of some neural network layers , Thus reducing the risk of over fitting . From a deeper understanding , As shown in the figure below , If you use tanh As an activation function ,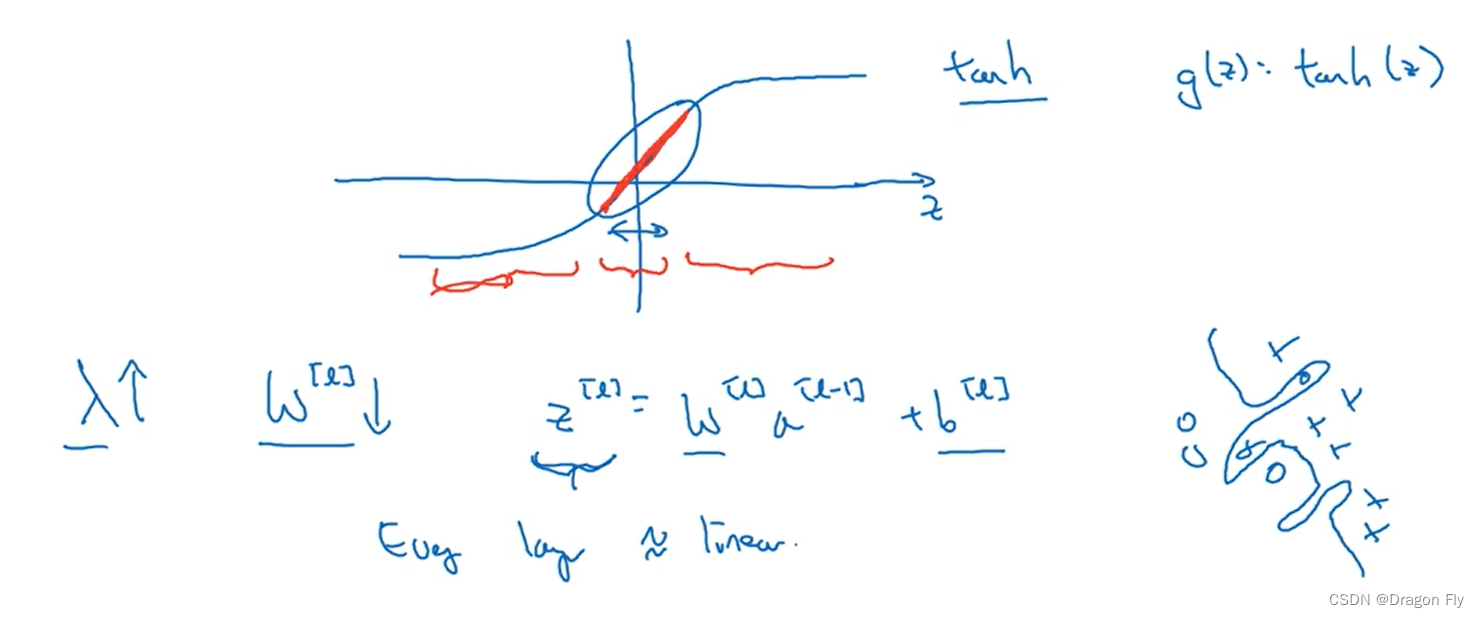

\qquad increase $\lambda$ The value of will make the value of the weight $w$ Reduce , Thus, the calculated value of neural network $z$ Reduce , about tanh Activation function ,$z$ A decrease in value means that the activation function is approximately a linear function , Therefore, it will not make the neural network learn very complex high-order functions , Thus reducing the risk of over fitting .

4.2 Drop out normalization

\qquad Drop The basic idea of is to reduce the number of neurons in each layer of neural network randomly or by a certain number , Thus reducing the risk of over fitting .Inverted dropout The execution process of is as follows ：

\qquad among ,$d_3$ The proportion of neurons that need to be removed is 20%, Then calculate the new neuron input value of the current neural network layer $a_3$, Finally, in order to make dropout Before and after , The neural network calculation value of the current layer remains roughly unchanged , Need to put dropout The neuron input value of is divided by $0.8$. When training data, we usually use dropout, But when testing data , Usually do not use dropout, Because random factors will be introduced , Make the test results fluctuate greatly .

4.3 Other normalization methods

\qquad data argument It can be used as a method to prevent over fitting , For example, in the field of image recognition , By way of input data Simple horizontal transformation operation for various pictures of , Increase the number of data sets , To prevent over fitting .
\qquad early stopping Another way to prevent over fitting , When the training error of the training set decreases , The error of cross validation set can increase , In this case , The training can be terminated where the error of cross validation set is the smallest , So as to place the over fitting .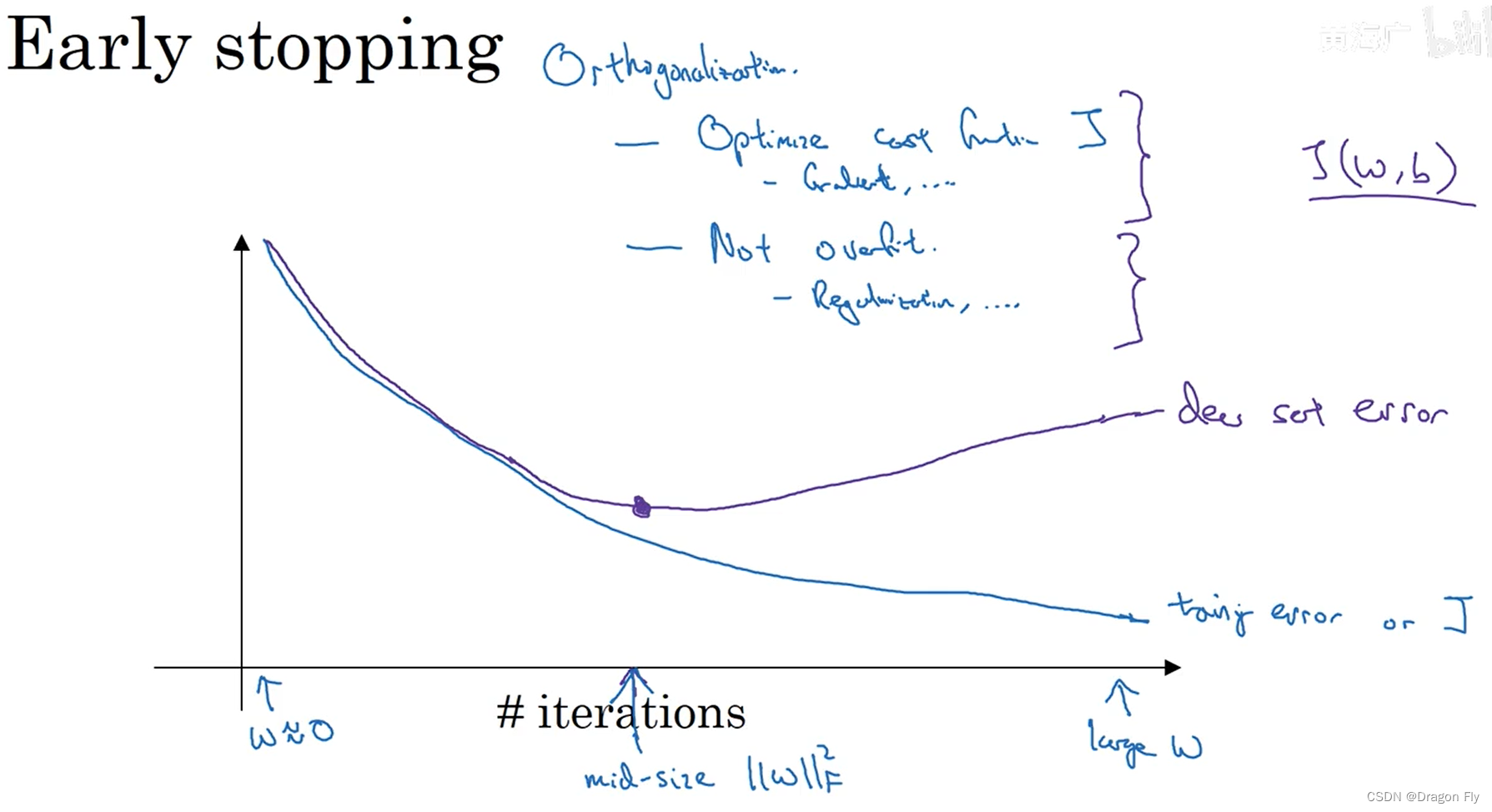

5、 Set questions to speed up model training

5.1 Normalized data set

\qquad Normalized data set features The method can first subtract the mean value from the input data (mean), Then normalize the variance (various).
$$\begin{gathered} \mu =\frac{1}{m}\sum _{i=1}^m{x}^i \\ x:=x-\mu \\ {\sigma }^2=\frac{1}{m}\sum _{i=1}^m(x^i{)}^2 \\ x:=x/\sigma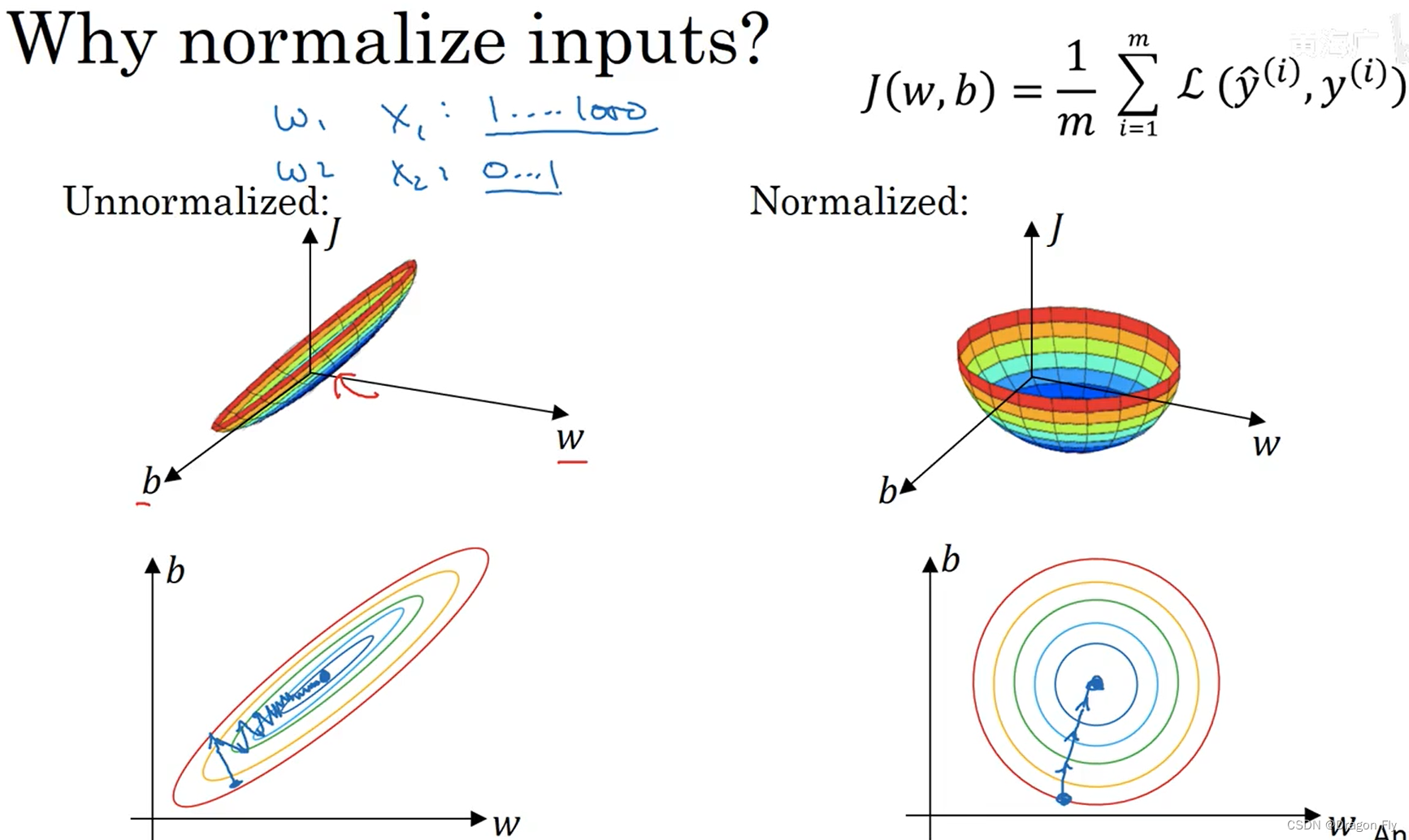 \end{gathered}$$

\qquad When the characteristic value ranges of training data are very different , It is necessary to features Normalize , Thus, the number of echelon descent execution is less , At the same time, it can increase the learning rate to improve the learning efficiency .

5.2 Gradient vanishing and gradient exploding

\qquad When training deep networks , Gradient disappearance and gradient explosion are easy to occur , As shown in the figure below ：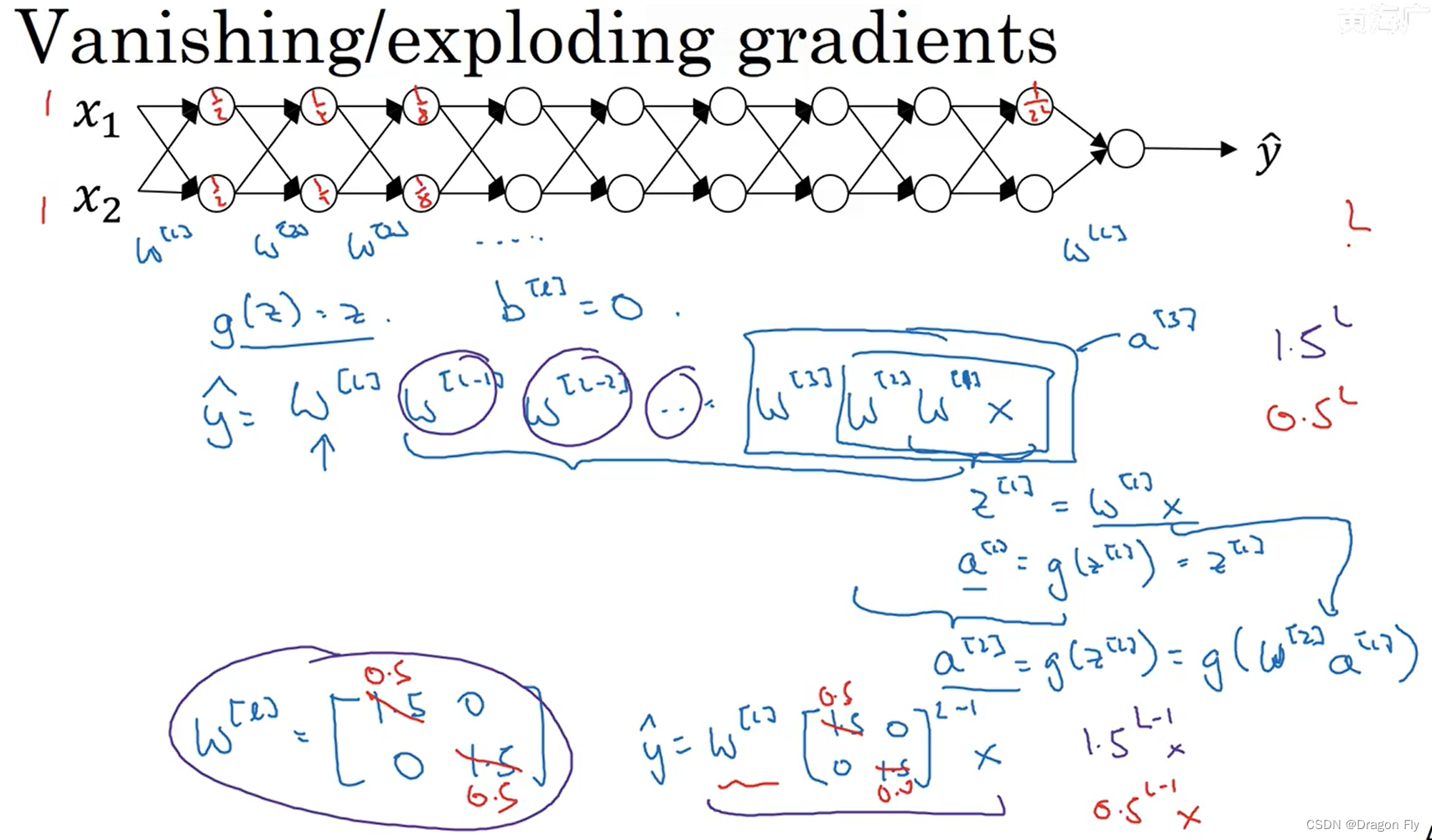

\qquad The problem of gradient disappearance and gradient explosion can be solved by carefully Initialize weights to get relief . If you use ReLU As an activation function , Usually, the network weight is initialized to $\frac{2}{n^{l-1}}$, When using tanh As an activation function , Usually use $\sqrt{\frac{1}{n^{l-1}}}$ As the initial value of network weight .

5.3 Gradient inspection

\qquad When using gradient test , The accuracy of bilateral test is higher than that of unilateral test .

\qquad The method of gradient test is as follows , By calculating the value of the approximate numerical gradient and the gradient value calculated by back propagation “ Euclidean distance ” To see if the gradient is calculated correctly .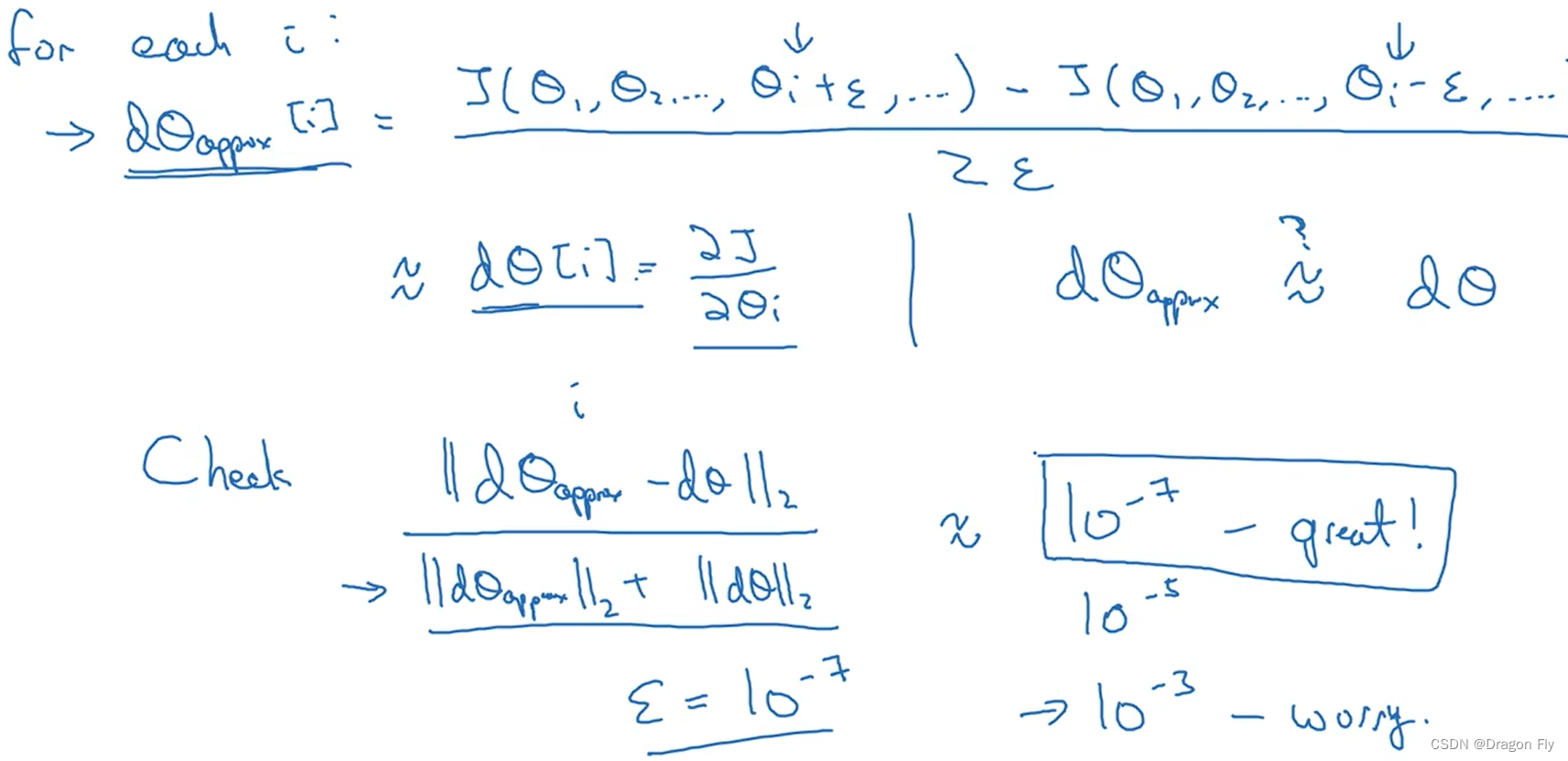

THE END