【力扣刷题】32. 最长有效括号

目录

题目：

方法一：

解题思路：

代码：

方法二：

解题思路：

代码：

题目：

给你一个只包含 '(' 和 ')' 的字符串，找出最长有效（格式正确且连续）括号子串的长度。

方法一：

解题思路：

利用栈，学过利用栈来判断一个只包含'('和')'的字符串是否是括号匹配的，那个题目解题就是，遍历整个字符串，是左括号就入栈，是右括号则①判断栈是否有左括号且弹出一个左括号，②如果栈为空则为false，如果所有字符都遍历完了，栈中还有元素则为false，否则为true。

利用这个思路，增加一个标记数组arr，初始化所有元素为1，栈中存的是数组下标（字符索引）。遍历整个字符串，如果是左括号则把索引下标（i）加入栈，如果是右括号则判断栈中元素是否为空且不为空则弹出，并把标记数组对应的元素arr[stack.pop()]以及当前下标对应的标记数组元素arr[i]置为0。

最后判断标记数组arr的最长连续0就可以了。

代码：

class Solution {
    public int longestValidParentheses(String s) {
        //要找最长的有效括号
        //栈
        //利用栈来标记左右括号是否有效，栈的内容存下标i
        Stack<Integer> stack = new Stack<>();
        int[] valid = new int[s.length()];
        for(int i = 0; i < s.length(); i++){
            valid[i] = 1;
        }
        for(int i = 0; i < s.length();i++){
            if(s.charAt(i) == '(') stack.push(i);
            else{
                if(!stack.empty()){
                    valid[i] = 0;
                    valid[stack.pop()] = 0;
                }
            }
        }
        int res = 0,count = 0;
        for(int i = 0; i < s.length();i++){
            if(valid[i] == 1) {
                count = 0;
            }else{
                count++;
            }
            res = Math.max(res,count);
        }
        return res;
    }
}

方法二：

解题思路：

动态规划，利用dp[i]表示以下标i字符结尾的最长有效括号的长度。将dp数组全部初始化为0。有效的子串一定以')'结尾，以'('结尾的子串对应的dp值必定为0。所以只需要求解以')'在dp数组中对应位置的值。所以从前往后遍历字符串，求解dp值。

①s.charAt(i)=')'且s.charAt(i-1)='('，字符串为"...()"则dp[i] = dp[i-2]+2。

②如果s.charAt(i) = ')'且s.charAt(i-1) = ')'，比如字符串"...))"->"()(())"，

如果s.charAt(i - dp[i - 1] - 1)='('，那么有效括号长度新增长度2，i位置对最长有效括号长度为 i-1位置的最长括号长度加上当前位置新增的2，不过得注意，i − dp[i − 1] − 1 和 i 组成了有效括号对，这将是一段独立的有效括号序列，如果之前的子序列是形如 (...)(...) 这种序列，那么当前位置的最长有效括号长度还需要加上这一段。例如：()(())，左边红色的和右边绿色的为两个独立的有效括号序列。所以状态转移方程为：dp[i] = dp[i - 1] + 2 + dp[i - dp[i - 1] -2 ]。

图示： 

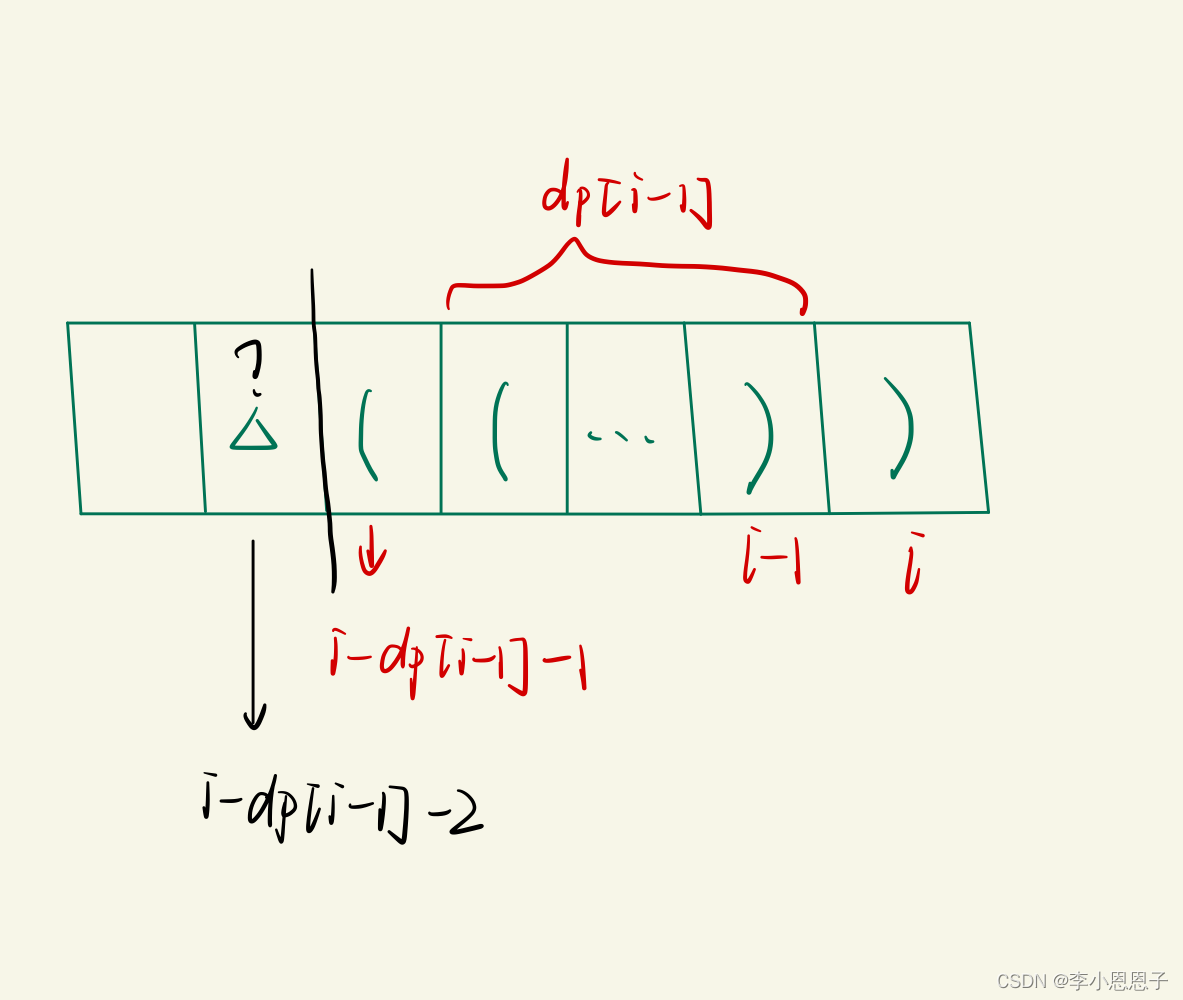
还要注意边界值，因为要用到 dp[ i - 2 ]，还有dp[ i - dp[ i - 1 ] - 2 ]，要判断。  

代码：

class Solution {
    public int longestValidParentheses(String s) {
        //动态规划
        //dp[i]表示以下标i字符结尾的最长有效括号的长度
        int res = 0;
        int[] dp = new int[s.length()];
        for(int i = 1;i < s.length();i++){
            if(s.charAt(i) == ')'){
                if(s.charAt(i-1) == '('){
                    if(i >= 2) dp[i] = dp[i - 2] + 2;
                    else dp[i] = 2;
                }else if(i - dp[i - 1] > 0  && s.charAt(i - dp[i - 1] - 1) == '('){
                    if(i - dp[i - 1] >= 2) dp[i] = dp[i - 1] + dp[i - dp[i - 1] - 2] + 2;
                    else dp[i] = dp[i - 1] + 2;
                }
            }
            res = Math.max(res,dp[i]);
        }
        return res;
    }
}

方法二看了看解析，不太会写动态规划，下次找个机会专门练一练动态规划的题目。