当前位置:网站首页>堆(優先級隊列)
堆(優先級隊列)
2022-07-02 12:07:00 【菜菜不恰菜】

目錄
🥬堆的性質

總結:一顆完全二叉樹以層序遍曆方式放入數組中存儲,這種方式的主要用法就是堆的錶示。
🥬堆的分類
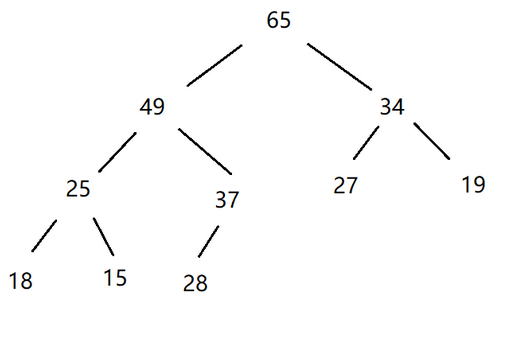

🥬堆的向下調整
現在有一個數組,邏輯上是完全二叉樹,我們通過從根節點開始的向下調整算法可以把它調整成一個小堆或者大堆。向下調整算法有一個前提:左右子樹必須是一個堆,才能調整。
以小堆為例:
1、先讓左右孩子結點比較,取最小值。
2、用較小的那個孩子結點與父親節點比較,如果孩子結點<父親節點,交換,反之,不交換。
3、循環往複,如果孩子結點的下標越界,則說明已經到了最後,就結束。
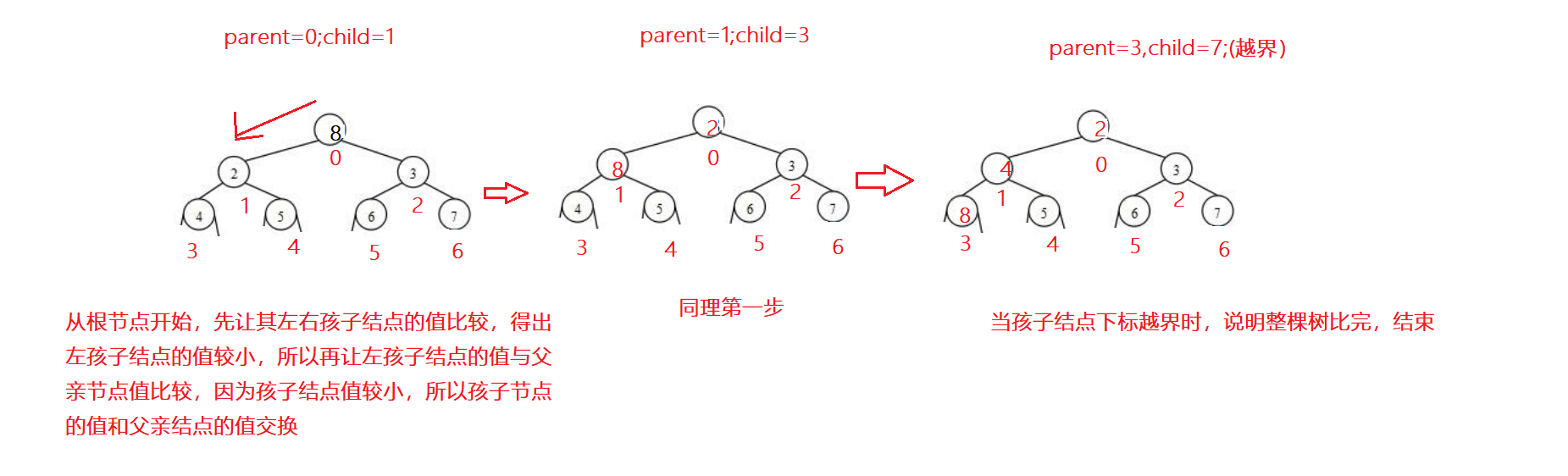
代碼示例:
//parent: 每棵樹的根節點
//len: 每棵樹的調整的結束比特置
public void shiftDown(int parent,int len){
int child=parent*2+1; //因為堆是完全二叉樹,沒有左孩子就一定沒有右孩子,所以最起碼是有左孩子的,至少有1個孩子
while(child<len){
if(child+1<len && elem[child]<elem[child+1]){
child++;//兩孩子結點比較取較小值
}
if(elem[child]<elem[parent]){
int tmp=elem[parent];
elem[parent]=elem[child];
elem[child]=tmp;
parent=child;
child=parent*2+1;
}else{
break;
}
}
}🥬堆的建立
public void creatHeap(int[] arr){
for(int i=0;i<arr.length;i++){
elem[i]=arr[i];
useSize++;
}
for(int parent=(useSize-1-1)/2;parent>=0;parent--){//數組下標從0開始
shiftDown(parent,useSize);
}
}建堆的空間複雜度為O(N),因為堆為一棵完全二叉樹,滿二叉樹也是一種完全二叉樹,我們用滿二叉樹(最壞情况下)來證明。
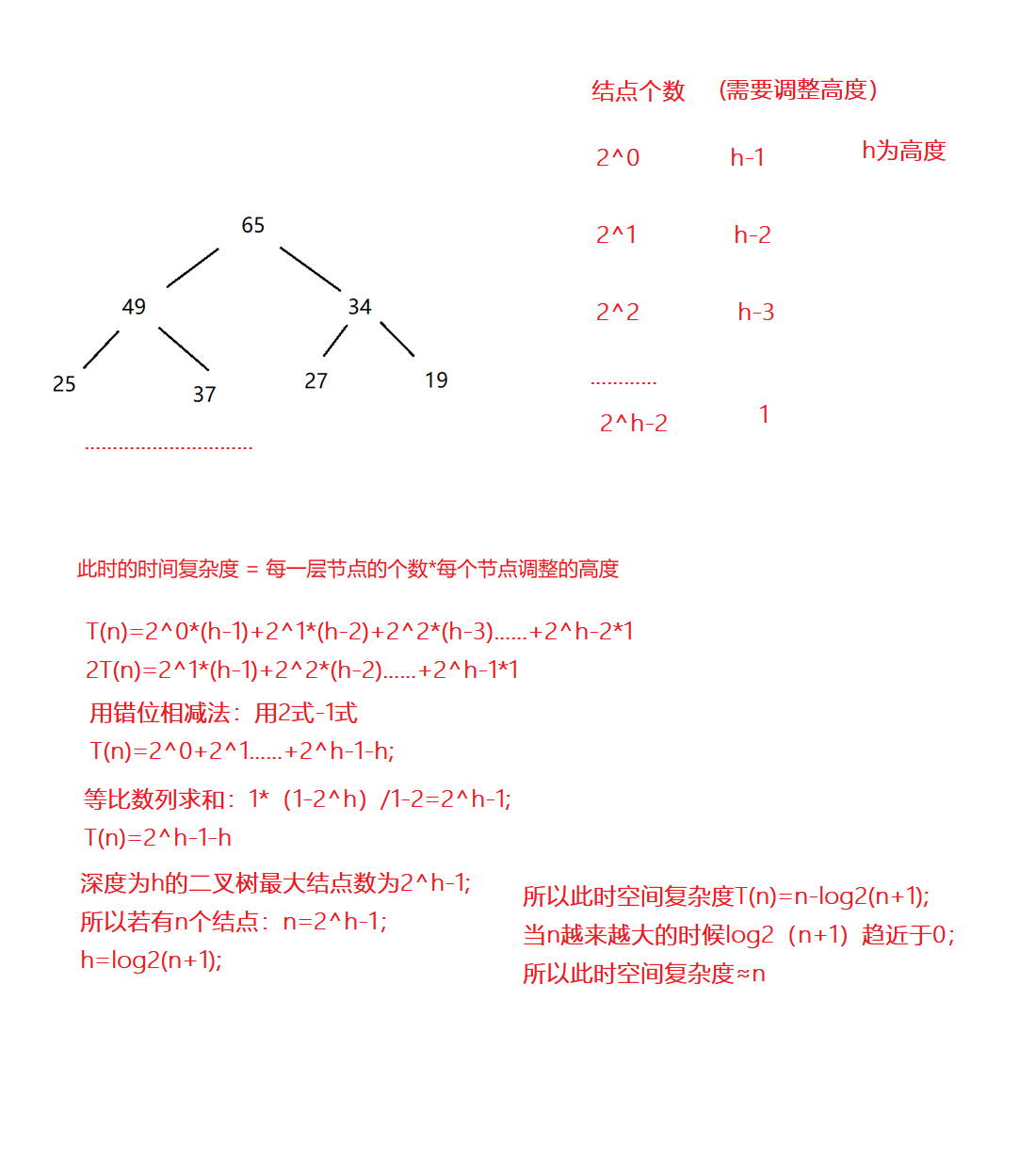
🥬堆得向上調整
現在有一個堆,我們需要在堆的末尾插入數據,再對其進行調整,使其仍然保持堆的結構,這就是向上調整。
以大堆為例:

代碼示例:
public void shiftup(int child){
int parent=(child-1)/2;
while(child>0){
if(elem[child]>elem[parent]){
int tmp=elem[parent];
elem[parent]=elem[child];
elem[child]=tmp;
child=parent;
parent=(child-1)/2;
}else{
break;
}
}
}🥬堆的常用操作
入隊列
往堆裏面加入元素,就是往最後一個比特置加入,然後在進行向上調整。
public boolean isFull(){
return elem.length==useSize;
}
public void offer(int val){
if(isFull()){
elem= Arrays.copyOf(elem,2*elem.length);//擴容
}
elem[useSize++]=val;
shiftup(useSize-1);
}出隊列
把堆裏元素删除,就把堆頂元素和最後一個元素交換,然後向整個數組大小减一,最後向下調整,就删除了棧頂元素。
public boolean isEmpty(){
return useSize==0;
}
public int poll(){
if(isEmpty()){
throw new RuntimeException("優先級隊列為空");
}
int tmp=elem[0];
elem[0]=elem[useSize-1];
elem[useSize-1]=tmp;
useSize--;
shiftDown(0,useSize);
return tmp;
}獲取隊首元素
public int peek() {
if (isEmpty()) {
throw new RuntimeException("優先級隊列為空");
}
return elem[0];
}🥬TopK 問題
給你6個數據,求前3個最大數據。這時候我們用堆怎麼做的?
解題思路:
1、如果求前K個最大的元素,要建一個小根堆。
2、如果求前K個最小的元素,要建一個大根堆。
3、第K大的元素。建一個小堆,堆頂元素就是第K大的元素。
4、第K小的元素。建一個大堆,堆頂元素就是第K大的元素。
舉個例子:求前n個最大數據

代碼示例:
public static int[] topK(int[] array,int k){
//創建一個大小為K的小根堆
PriorityQueue<Integer> minHeap=new PriorityQueue<>(k, new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
return o1-o2;
}
});
//遍曆數組中元素,將前k個元素放入隊列中
for(int i=0;i<array.length;i++){
if(minHeap.size()<k){
minHeap.offer(array[i]);
}else{
//從k+1個元素開始,分別和堆頂元素比較
int top=minHeap.peek();
if(array[i]>top){
//先彈出後存入
minHeap.poll();
minHeap.offer(array[i]);
}
}
}
//將堆中元素放入數組中
int[] tmp=new int[k];
for(int i=0;i< tmp.length;i++){
int top=minHeap.poll();
tmp[i]=top;
}
return tmp;
}
public static void main(String[] args) {
int[] array={12,8,23,6,35,22};
int[] tmp=topK(array,3);
System.out.println(Arrays.toString(tmp));
}結果:
數組排序
再者說如果要對一個數組進行從小到大排序,要借助大根堆還是小根堆呢?
---->大根堆
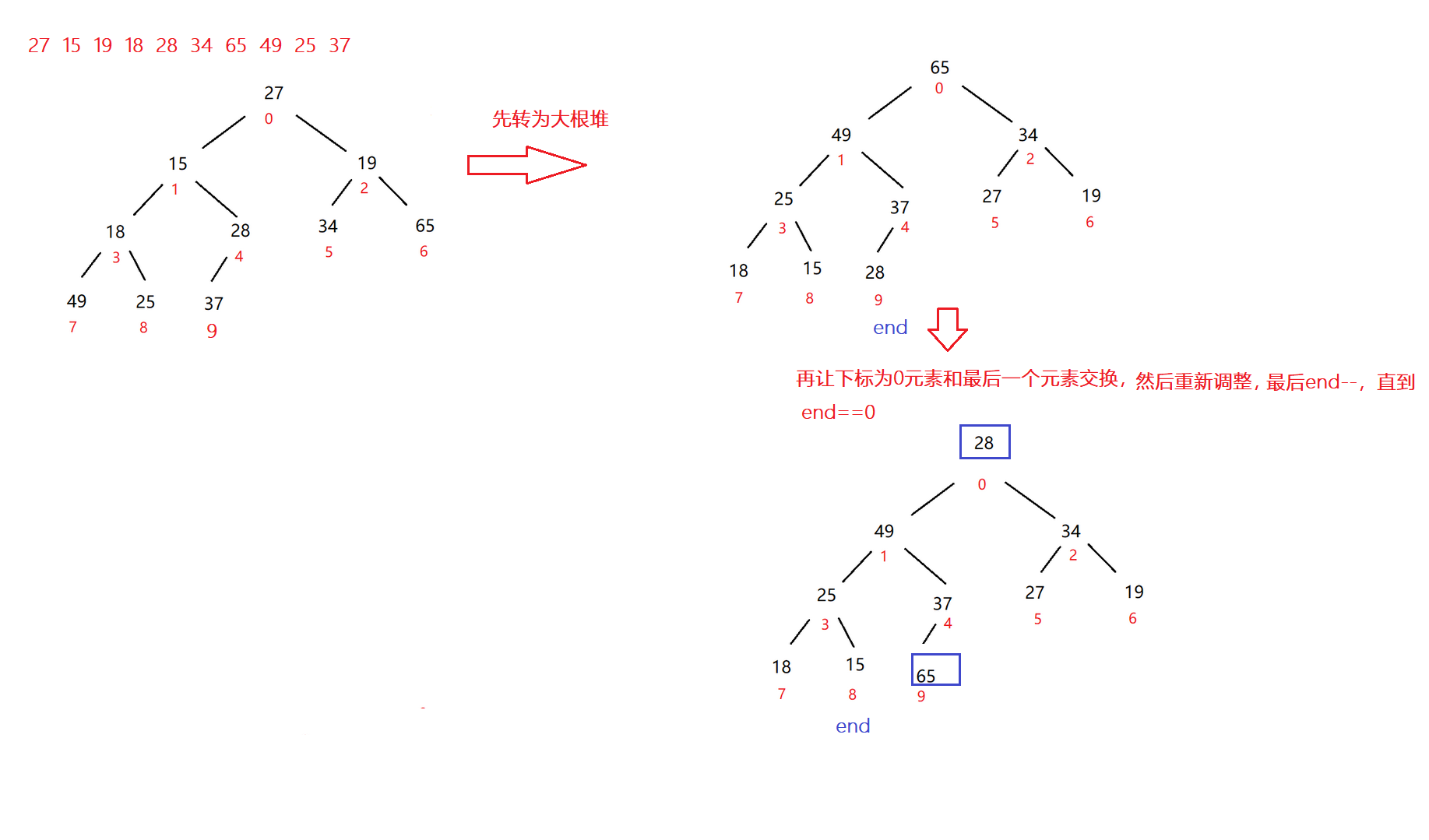
代碼示例:
public void heapSort(){
int end=useSize-1;
while(end>0){
int tmp=elem[0];
elem[0]=elem[end];
elem[end]=tmp;
shiftDown(0,end);//假設這裏向下調整為大根堆
end--;
}
}🥬小結
以上就是今天的內容了,有什麼問題可以在評論區留言

边栏推荐
- 数据分析 - matplotlib示例代码
- Seriation in R: How to Optimally Order Objects in a Data Matrice
- Le tutoriel F - String le plus facile à comprendre de l'histoire.
- SCM power supply
- K-Means Clustering Visualization in R: Step By Step Guide
- Jenkins user rights management
- PgSQL string is converted to array and associated with other tables, which are displayed in the original order after matching and splicing
- 深入理解PyTorch中的nn.Embedding
- [QT] Qt development environment installation (QT version 5.14.2 | QT download | QT installation)
- easyExcel和lombok注解以及swagger常用注解
猜你喜欢
![[visual studio 2019] create and import cmake project](/img/51/6c2575030c5103aee6c02bec8d5e77.jpg)
[visual studio 2019] create and import cmake project

ES集群中节点与分片的区别
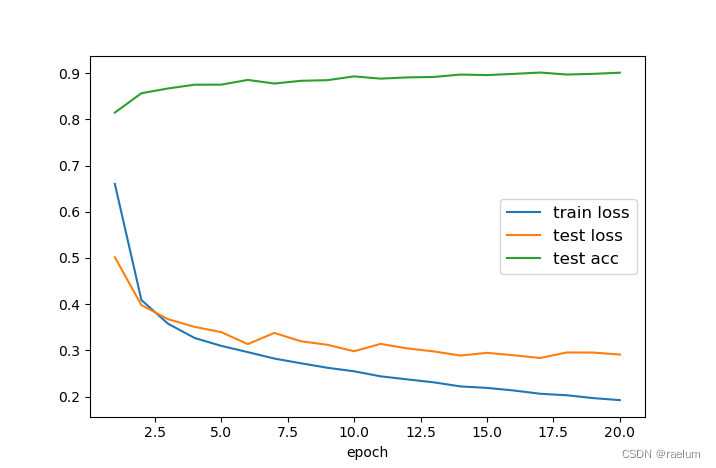
PyTorch搭建LSTM实现服装分类(FashionMNIST)

Depth filter of SvO2 series

How to Create a Beautiful Plots in R with Summary Statistics Labels

【2022 ACTF-wp】
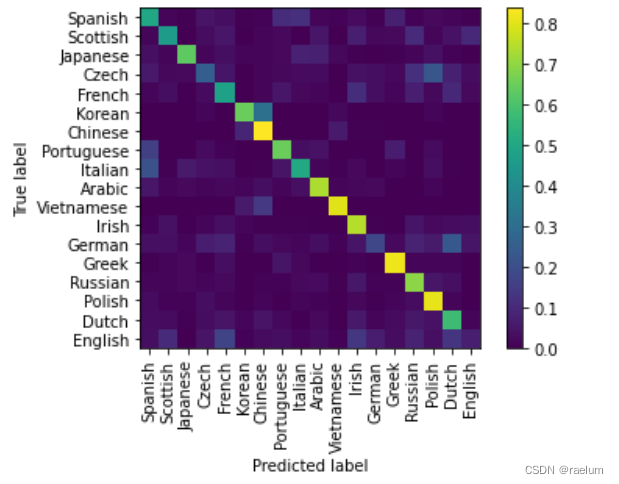
Natural language processing series (II) -- building character level language model using RNN
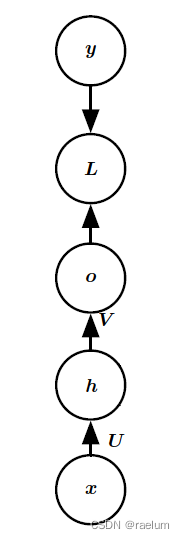
自然语言处理系列(一)——RNN基础
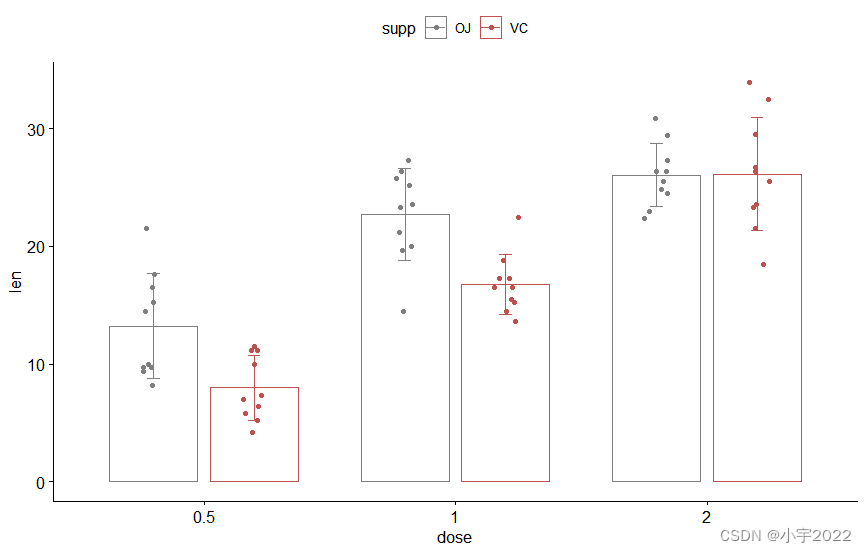
HOW TO EASILY CREATE BARPLOTS WITH ERROR BARS IN R

HOW TO CREATE A BEAUTIFUL INTERACTIVE HEATMAP IN R
随机推荐
Orb-slam2 data sharing and transmission between different threads
排序---
Le tutoriel F - String le plus facile à comprendre de l'histoire.
ESP32 Arduino 引入LVGL 碰到的一些问题
QT meter custom control
测试左移和右移
Test shift left and right
Leetcode922 按奇偶排序数组 II
【工控老马】西门子PLC Siemens PLC TCP协议详解
Thesis translation: 2022_ PACDNN: A phase-aware composite deep neural network for speech enhancement
求16以内正整数的阶乘,也就是n的阶层(0=<n<=16)。输入1111退出。
CMake交叉编译
二分刷题记录(洛谷题单)区间的甄别
字符串回文hash 模板题 O(1)判字符串是否回文
Enter the top six! Boyun's sales ranking in China's cloud management software market continues to rise
HOW TO ADD P-VALUES ONTO A GROUPED GGPLOT USING THE GGPUBR R PACKAGE
Easyexcel and Lombok annotations and commonly used swagger annotations
Leetcode122 the best time to buy and sell stocks II
PgSQL string is converted to array and associated with other tables, which are displayed in the original order after matching and splicing
CONDA common command summary