LineSegmentTree线段树

参考链接

线段树详解 (lfool.github.io)

Range模块【线段树动态开点+线段树图解】 - Range 模块 - 力扣（LeetCode）

引入

线段树解决的是「区间和」的问题，且该「区间」会被修改

什么意思呢？举个简单的例子，对于 nums = [1, 2, 3, 4, 5]

如果我们需要多次求某一个区间的和，是不是首先想到了利用「前缀和」。关于前缀和的详细介绍可见 [前缀和数组])

但是如果 nums 会被修改呢？比如：

• 把第 i 个元素修改成 x
• 把第 i 个元素增加 x
• 把区间 [i, j] 内的元素都增加 x

此时，如果我们再使用「前缀和」，就没那么高效了。因为每一次更新，前缀和数组必须也随之更新，时间复杂度为 O(n)

既然「前缀和」在这种场景下没那么高效了，所以就有了今天要介绍的「线段树」

原理

上面提到过：线段树解决的是「区间和」的问题，且该「区间」会被修改

所以线段树主要实现两个方法：「求区间和」&&「修改区间」，且时间复杂度均为 O(logn)

始终记住一句话：线段树的每个节点代表一个区间

nums = [1, 2, 3, 4, 5] 对应的线段树如下所示：

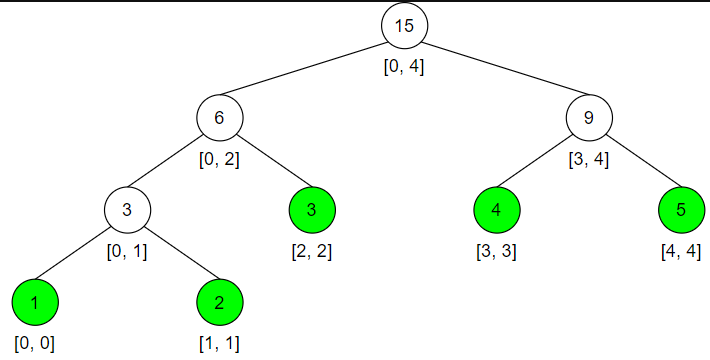
从图中可以看到，每个节点代表一个区间，而节点的值就是该区间的和 (其实还可以根据题目问题，改变表示的含义！！)

• 数字之和「总数字之和 = 左区间数字之和 + 右区间数字之和」
• 最大公因数 (GCD)「总 GCD = gcd(左区间 GCD, 右区间 GCD)」
• 最大值「总最大值 = max(左区间最大值，右区间最大值)」

不符合区间加法的例子：

• 众数「只知道左右区间的众数，没法求总区间的众数」
• 01 序列的最长连续零「只知道左右区间的最长连续零，没法知道总的最长连续零」

根节点代表的区间是问题的总区间，如这个例子，问题的总区间就是数组的长度 [0, 4]

其实线段树是一棵近似的完全二叉树，该例子就是一棵完全二叉树，但是有些情况不是完全二叉树

所以对于给定的一个问题，如果该问题的范围是确定的，那么该问题的线段树也是确定的，因为建立线段树的过程就是不断把区间「平分」的过程，直到区间长度为 1

注意：下面的所有实现均基于求「区间和」以及对区间进行「加减」的更新操作

线段树的数据结构

我们可以使用数组来表示一棵线段树，假如根节点为 i，那么左孩子的节点就为 2 * i，右孩子的节点就为 2 * i + 1 (前提：i 从 1 开始)

我们可以使用链表来表示一棵线段树，其节点的数据结构如下：

class Node {
    
    // 左右孩子节点
    Node left, right;
    // 当前节点值
    int val;
}

个人比较倾向使用链表，因为比较节约内存，下面的实现均基于链表

线段树的建立

如果题目中给了具体的区间范围，我们根据该范围建立线段树。见题目 区域和检索 - 数组可修改

public void buildTree(Node node, int start, int end) {
    
    // 到达叶子节点
    if (start == end) {
    
        node.val = arr[start];
        return ;
    }
    int mid = (start + end) >> 1;
    buildTree(node.left, start, mid);
    buildTree(node.right, mid + 1, end);
    // 向上更新
    pushUp(node);
}
// 向上更新
private void pushUp(Node node) {
    
    node.val = node.left.val + node.right.val;
}

但是很多时候，题目中都没有给出很具体的范围，只有数据的取值范围，一般都很大，所以我们更常用的是「动态开点」

下面我们手动模拟一下「动态开点」的过程。同样的，也是基于上面的例子 nums = [1, 2, 3, 4, 5]

假设一种情况，最开始只知道数组的长度 5，而不知道数组内每个元素的大小，元素都是后面添加进去的。所以线段树的初始状态如下图所示：(只有一个节点，很孤独！！)

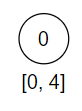
假设此时，我们添加了一个元素 [2, 2]; val = 3。现在线段树的结构如下图所示：

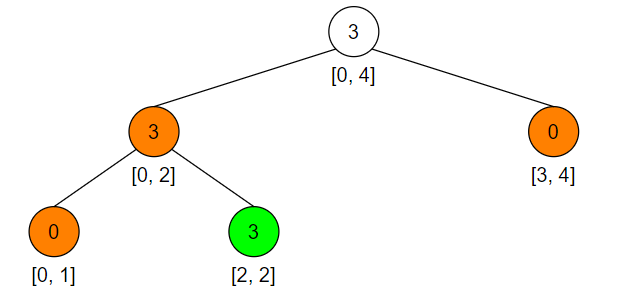
这里需要解释一下，如果一个节点没有左右孩子，会一下子把左右孩子节点都给创建出来，如上图橙色节点所示，具体代码可见方法 pushDown()

两个橙色的叶子节点仅仅只是被创建出来了，并无实际的值，均为 0；而另外一个橙色的非叶子节点，值为 3 的原因是下面的孩子节点的值向上更新得到的

下面给出依次添加剩余节点的过程：(注意观察值的变化！！)

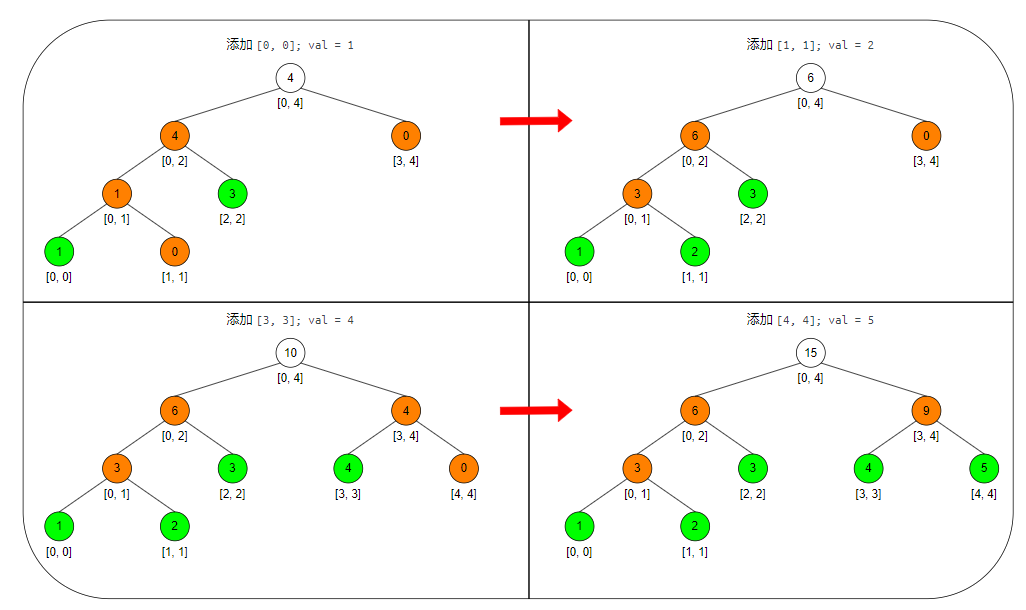
「动态开点」一般是在「更新」或「查询」的时候动态的建立节点，具体可见下面的更新和查询操作

线段树的更新

我看大多数教程都是把更新分为两种：「点更新」和「区间更新」。其实这两种可以合并成一种，「点更新」不就是更新长度为 1 的区间嘛！！

更新区间的前提是找到需要更新的区间，所以和查询的思路很相似

如果我们要把区间 [2, 4] 内的元素都「1」

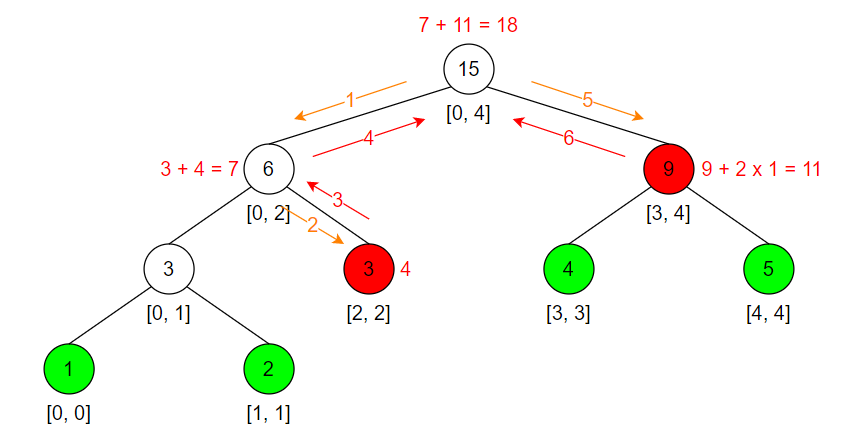
我们会发现一个很有意思的现象，我们只把 [2,2] 和 [3,4] 这两个区间对应的节点更新了，而区间 [3, 3] 和 [4,4] 并没有更新

按道理来说，[3, 3] 和 [4,4] 也是需要更新的，不然当我们查询区间 [3, 3] 和 [4,4] 的值，就会出现错误！！

这是因为我们使用了「懒惰标记」的方法，我们只需要更新到满足条件的区间即可，然后再给该区间对应的节点加一个懒惰标记，表示该节点所有对应的孩子节点都应该有此更新

当我们向孩子节点遍历的时候会把「懒惰标记」下推给孩子节点

我们需要稍微修改一下 Node 的数据结构

class Node {
    
    // 左右孩子节点
    Node left, right;
    // 当前节点值
    int val;
    // 懒惰标记
    int add;
}

基于「动态开点」的前提，我们下推懒惰标记的时候，如果节点不存在左右孩子节点，那么我们就创建左右孩子节点

先来实现下推懒惰标记的函数：

// leftNum 和 rightNum 表示左右孩子区间的叶子节点数量
// 因为如果是「加减」更新操作的话，需要用懒惰标记的值️叶子节点的数量
private void pushDown(Node node, int leftNum, int rightNum) {
    
    // 动态开点
    if (node.left == null) node.left = new Node();
    if (node.right == null) node.right = new Node();
    // 如果 add 为 0，表示没有标记
    if (node.add == 0) return ;
    // 注意：当前节点加上标记值️该子树所有叶子节点的数量
    node.left.val += node.add * leftNum;
    node.right.val += node.add * rightNum;
    // 把标记下推给孩子节点
    // 对区间进行「加减」的更新操作，下推懒惰标记时需要累加起来，不能直接覆盖
    node.left.add += node.add;
    node.right.add += node.add;
    // 取消当前节点标记
    node.add = 0;
}

下面来实现更新的函数：

public void update(Node node, int start, int end, int l, int r, int val) {
    
    // 找到满足要求的区间
    if (l <= start && end <= r) {
    
        // 区间节点加上更新值
        // 注意：需要️该子树所有叶子节点
        node.val += (end - start + 1) * val;
        // 添加懒惰标记
        // 对区间进行「加减」的更新操作，懒惰标记需要累加，不能直接覆盖
        node.add += val;
        return ;
    }
    int mid = (start + end) >> 1;
    // 下推标记
    // mid - start + 1：表示左孩子区间叶子节点数量
    // end - mid：表示右孩子区间叶子节点数量
    pushDown(node, mid - start + 1, end - mid);
    // [start, mid] 和 [l, r] 可能有交集，遍历左孩子区间
    if (l <= mid) update(node.left, start, mid, l, r, val);
    // [mid + 1, end] 和 [l, r] 可能有交集，遍历右孩子区间
    if (r > mid) update(node.right, mid + 1, end, l, r, val);
    // 向上更新
    pushUp(node);
}

线段树的查询

如果我们要查询区间 [2, 4] 的结果，如下图红色标记所示：

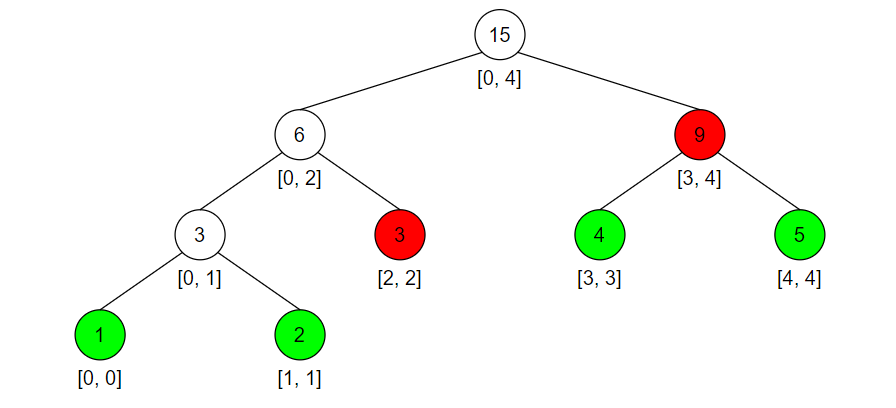
下面给出代码实现：

// 在区间 [start, end] 中查询区间 [l, r] 的结果，即 [l ,r] 保持不变
// 对于上面的例子，应该这样调用该函数：query(root, 0, 4, 2, 4)
public int query(Node node, int start, int end, int l, int r) {
    
    // 区间 [l ,r] 完全包含区间 [start, end]
    // 例如：[2, 4] = [2, 2] + [3, 4]，当 [start, end] = [2, 2] 或者 [start, end] = [3, 4]，直接返回
    if (l <= start && end <= r) return node.val;
    // 把当前区间 [start, end] 均分得到左右孩子的区间范围
    // node 左孩子区间 [start, mid]
    // node 左孩子区间 [mid + 1, end]
    int mid = (start + end) >> 1, ans = 0;
    // 下推标记
    pushDown(node, mid - start + 1, end - mid);
    // [start, mid] 和 [l, r] 可能有交集，遍历左孩子区间
    if (l <= mid) ans += query(node.left, start, mid, l, r);
    // [mid + 1, end] 和 [l, r] 可能有交集，遍历右孩子区间
    if (r > mid) ans += query(node.right, mid + 1, end, l, r);
    // ans 把左右子树的结果都累加起来了，与树的后续遍历同理
    return ans;
}

完整模版

注意：下面模版基于求「区间和」以及对区间进行「加减」的更新操作，且为「动态开点」

/** * @Description: 线段树（动态开点）纯净版 * @Author: Ladidol * @Date 2022年7月20日14:20:45 **/
public class SegmentTreeDynamic {
    
    class Node {
    
        Node left, right;
        int val, add;
    }
    private int N = (int) 1e9;
    private Node root = new Node();
    public void update(Node node, int start, int end, int l, int r, int val) {
    
        if (l <= start && end <= r) {
    
            node.val += (end - start + 1) * val;
            node.add += val;
            return ;
        }
        int mid = (start + end) >> 1;
        pushDown(node, mid - start + 1, end - mid);
        if (l <= mid) update(node.left, start, mid, l, r, val);
        if (r > mid) update(node.right, mid + 1, end, l, r, val);
        pushUp(node);
    }
    public int query(Node node, int start, int end, int l, int r) {
    
        if (l <= start && end <= r) return node.val;
        int mid = (start + end) >> 1, ans = 0;
        pushDown(node, mid - start + 1, end - mid);
        if (l <= mid) ans += query(node.left, start, mid, l, r);
        if (r > mid) ans += query(node.right, mid + 1, end, l, r);
        return ans;
    }
    private void pushUp(Node node) {
    
        node.val = node.left.val + node.right.val;
    }
    private void pushDown(Node node, int leftNum, int rightNum) {
    
        if (node.left == null) node.left = new Node();
        if (node.right == null) node.right = new Node();
        if (node.add == 0) return ;
        node.left.val += node.add * leftNum;
        node.right.val += node.add * rightNum;
        // 对区间进行「加减」的更新操作，下推懒惰标记时需要累加起来，不能直接覆盖
        node.left.add += node.add;
        node.right.add += node.add;
        node.add = 0;
    }
}

再次强调一遍：上面给出的模版基于求「区间和」以及对区间进行「加减」的更新操作，且为「动态开点」

但是下面给出的题目实战中，有些题目需要对模版进行小小的修改 (很多人问这个问题，这里统一整理汇总一下！！)

• 对于表示为「区间和」且对区间进行「加减」的更新操作的情况，我们在更新节点值的时候『需要️左右孩子区间叶子节点的数量 (注意是叶子节点的数量)』；我们在下推懒惰标记的时候『需要累加』！！(这种情况和模版一致！！) 如题目 最近的请求次数
• 对于表示为「区间和」且对区间进行「覆盖」的更新操作的情况，我们在更新节点值的时候『需要️左右孩子区间叶子节点的数量 (注意是叶子节点的数量)』；我们在下推懒惰标记的时候『不需要累加』！！(因为是覆盖操作！！) 如题目 区域和检索 - 数组可修改
• 对于表示为「区间最值」且对区间进行「加减」的更新操作的情况，我们在更新节点值的时候『不需要️左右孩子区间叶子节点的数量 (注意是叶子节点的数量)』；我们在下推懒惰标记的时候『需要累加』！！ 如题目 我的日程安排表 I、我的日程安排表 III

注意：对于题目 最近的请求次数 和 区域和检索 - 数组可修改 可以「不用️左右孩子区间叶子节点的数量」

为什么？？因为这两个题目是「点更新」，在介绍线段树更新的时候，我们说过：「点更新」和「区间更新」可以合并成一种，「点更新」不就是更新长度为 1 的区间嘛！！

上面两个题目调用更新函数的方式为：update(root, 1, N, t, t, 1); 和 update(root, 0, N, i, i, nums[i]);

由于区间是一个点，所以一定会更新到叶子节点，故可以不用️左右孩子区间叶子节点的数量！！

题目实战

我的日程安排表 I

题目详情可见 我的日程安排表 I

该题目基于下面「我的日程安排表 III」的思路！！！

class MyCalendar {
    

    public MyCalendar() {
    

    }
    
    public boolean book(int start, int end) {
    
        // 先查询该区间是否为 0
        if (query(root, 0, N, start, end - 1) != 0) return false;
        // 更新该区间
        update(root, 0, N, start, end - 1, 1);
        return true;
    }
    // *************** 下面是模版 ***************
    class Node {
    
        // 左右孩子节点
        Node left, right;
        // 当前节点值，以及懒惰标记的值
        int val, add;
    }
    private int N = (int) 1e9;
    private Node root = new Node();
    public void update(Node node, int start, int end, int l, int r, int val) {
    
        if (l <= start && end <= r) {
    
            node.val += val;
            node.add += val;
            return ;
        }
        pushDown(node);
        int mid = (start + end) >> 1;
        if (l <= mid) update(node.left, start, mid, l, r, val);
        if (r > mid) update(node.right, mid + 1, end, l, r, val);
        pushUp(node);
    }
    public int query(Node node, int start, int end, int l, int r) {
    
        if (l <= start && end <= r) return node.val;
        pushDown(node);
        int mid = (start + end) >> 1, ans = 0;
        if (l <= mid) ans = query(node.left, start, mid, l, r);
        if (r > mid) ans = Math.max(ans, query(node.right, mid + 1, end, l, r));
        return ans;
    }
    private void pushUp(Node node) {
    
        // 每个节点存的是当前区间的最大值
        node.val = Math.max(node.left.val, node.right.val);
    }
    private void pushDown(Node node) {
    
        if (node.left == null) node.left = new Node();
        if (node.right == null) node.right = new Node();
        if (node.add == 0) return ;
        node.left.val += node.add;
        node.right.val += node.add;
        node.left.add += node.add;
        node.right.add += node.add;
        node.add = 0;
    }
}

我的日程安排表 II

题目详情可见 我的日程安排表 II

该题目基于下面「我的日程安排表 III」的思路！！！

class MyCalendarTwo {
    

    public MyCalendarTwo() {
    

    }
    
    public boolean book(int start, int end) {
    
        if (query(root, 0, N, start, end - 1) == 2) return false;
        update(root, 0, N, start, end - 1, 1);
        return true;
    }
    // *************** 下面是模版 ***************
    class Node {
    
        // 左右孩子节点
        Node left, right;
        // 当前节点值，以及懒惰标记的值
        int val, add;
    }
    private int N = (int) 1e9;
    private Node root = new Node();
    public void update(Node node, int start, int end, int l, int r, int val) {
    
        if (l <= start && end <= r) {
    
            node.val += val;
            node.add += val;
            return ;
        }
        pushDown(node);
        int mid = (start + end) >> 1;
        if (l <= mid) update(node.left, start, mid, l, r, val);
        if (r > mid) update(node.right, mid + 1, end, l, r, val);
        pushUp(node);
    }
    public int query(Node node, int start, int end, int l, int r) {
    
        if (l <= start && end <= r) return node.val;
        pushDown(node);
        int mid = (start + end) >> 1, ans = 0;
        if (l <= mid) ans = query(node.left, start, mid, l, r);
        if (r > mid) ans = Math.max(ans, query(node.right, mid + 1, end, l, r));
        return ans;
    }
    private void pushUp(Node node) {
    
        // 每个节点存的是当前区间的最大值
        node.val = Math.max(node.left.val, node.right.val);
    }
    private void pushDown(Node node) {
    
        if (node.left == null) node.left = new Node();
        if (node.right == null) node.right = new Node();
        if (node.add == 0) return ;
        node.left.val += node.add;
        node.right.val += node.add;
        node.left.add += node.add;
        node.right.add += node.add;
        node.add = 0;
    }
}

我的日程安排表 III

题目详情可见 我的日程安排表 III

上面说过「节点的值不止可以表示该区间的和」，还可以「表示为当前区间的最值」，该题目存储的就是区间的最大值

class MyCalendarThree {
    

    public MyCalendarThree() {
    

    }
    
    public int book(int start, int end) {
    
        // 只用到了 update
        update(root, 0, N, start, end - 1, 1);
        // 最大值即为根节点的值
        return root.val;
    }
    // *************** 下面是模版 ***************
    class Node {
    
        // 左右孩子节点
        Node left, right;
        // 当前节点值，以及懒惰标记的值
        int val, add;
    }
    private int N = (int) 1e9;
    private Node root = new Node();
    public void update(Node node, int start, int end, int l, int r, int val) {
    
        if (l <= start && end <= r) {
    
            node.val += val;
            node.add += val;
            return ;
        }
        pushDown(node);
        int mid = (start + end) >> 1;
        if (l <= mid) update(node.left, start, mid, l, r, val);
        if (r > mid) update(node.right, mid + 1, end, l, r, val);
        pushUp(node);
    }
    public int query(Node node, int start, int end, int l, int r) {
    
        if (l <= start && end <= r) return node.val;
        pushDown(node);
        int mid = (start + end) >> 1, ans = 0;
        if (l <= mid) ans = query(node.left, start, mid, l, r);
        if (r > mid) ans = Math.max(ans, query(node.right, mid + 1, end, l, r));
        return ans;
    }
    private void pushUp(Node node) {
    
        // 每个节点存的是当前区间的最大值
        node.val = Math.max(node.left.val, node.right.val);
    }
    private void pushDown(Node node) {
    
        if (node.left == null) node.left = new Node();
        if (node.right == null) node.right = new Node();
        if (node.add == 0) return ;
        node.left.val += node.add;
        node.right.val += node.add;
        node.left.add += node.add;
        node.right.add += node.add;
        node.add = 0;
    }
}

Range 模块

题目详情可见 Range 模块

每个节点的值表示当前区间是否被覆盖

class RangeModule {
    

    public RangeModule() {
    

    }
    
    public void addRange(int left, int right) {
    
        // 1 表示覆盖；-1 表示取消覆盖
        update(root, 1, N, left, right - 1, 1);
    }
    
    public boolean queryRange(int left, int right) {
    
        return query(root, 1, N, left, right - 1);
    }
    
    public void removeRange(int left, int right) {
    
        // 1 表示覆盖；-1 表示取消覆盖
        update(root, 1, N, left, right - 1, -1);
    }

    // *************** 下面是模版 ***************
    class Node {
    
        Node left, right;
        // 表示当前区间是否被覆盖
        boolean cover;
        int add;
    }
    private int N = (int) 1e9;
    private Node root = new Node();
    public void update(Node node, int start, int end, int l, int r, int val) {
    
        if (l <= start && end <= r) {
    
            // 1 表示覆盖；-1 表示取消覆盖
            node.cover = val == 1;
            node.add = val;
            return ;
        }
        int mid = (start + end) >> 1;
        pushDown(node, mid - start + 1, end - mid);
        if (l <= mid) update(node.left, start, mid, l, r, val);
        if (r > mid) update(node.right, mid + 1, end, l, r, val);
        pushUp(node);
    }
    public boolean query(Node node, int start, int end, int l, int r) {
    
        if (l <= start && end <= r) return node.cover;
        int mid = (start + end) >> 1;
        pushDown(node, mid - start + 1, end - mid);
        // 查询左右子树是否被覆盖
        boolean ans = true;
        if (l <= mid) ans = ans && query(node.left, start, mid, l, r);
        if (r > mid) ans = ans && query(node.right, mid + 1, end, l, r);
        return ans;
    }
    private void pushUp(Node node) {
    
        // 向上更新
        node.cover = node.left.cover && node.right.cover;
    }
    private void pushDown(Node node, int leftNum, int rightNum) {
    
        if (node.left == null) node.left = new Node();
        if (node.right == null) node.right = new Node();
        if (node.add == 0) return ;
        node.left.cover = node.add == 1;
        node.right.cover = node.add == 1;
        node.left.add = node.add;
        node.right.add = node.add;
        node.add = 0;
    }
}

区域和检索 - 数组可修改

题目详情可见 区域和检索 - 数组可修改

方法一：

class NumArray {
    

    private final int n;
    private final int[] arr;
    private final int[] tree;
    private final int[] add;

    public NumArray(int[] nums) {
    
        this.n = nums.length;
        this.arr = nums;
        // 必须开 4 倍长度的数组
        this.tree = new int[n << 2];
        this.add = new int[n << 2];
        buildTree(0, n - 1, 1);
    }
    
    public void update(int index, int val) {
    
        update(0, n - 1, 1, index, val);
    }
    
    public int sumRange(int left, int right) {
    
        return query(0, n - 1, left, right, 1);
    }

    public void updateRange(int l, int r, int val) {
    
        update(0, n - 1, 1, l, r, val);
    }

    private void buildTree(int start, int end, int rootId) {
    
        if (start == end) {
    
            tree[rootId] = arr[start];
            return ;
        }
        int mid = (start + end) >> 1;
        buildTree(start, mid, rootId << 1);
        buildTree(mid + 1, end, rootId << 1 | 1);
        pushUp(rootId);
    }
    private void update(int start, int end, int rootId, int updateIndex, int val) {
    
        if (start == end) {
    
            arr[start] = tree[rootId] = val;
            return ;
        }
        int mid = (start + end) >> 1;
        if (updateIndex > mid) {
    
            update(mid + 1, end, rootId << 1 | 1, updateIndex, val);
        } else {
    
            update(start, mid, rootId << 1, updateIndex, val);
        }
        pushUp(rootId);
    }
    private void update(int start, int end, int rootId, int l, int r, int val) {
    
        // 无交集
        if (r < start || l > end) return ;
        // 如果本区间完全在操作区间 [l, r] 以内
        else if (l <= start && end <= r) {
    
            // 更新数字和，向上保持正确
            tree[rootId] += val * (end - start + 1);
            // 增加 add 标记，表示本区间的 Sum 正确，子区间的 Sum 仍需要根据 add 的值来调整
            add[rootId] += val;
            return ;
        }
        int mid = (start + end) >> 1;
        // 下推标记
        pushDown(rootId, mid - start + 1, end - mid);
        update(start, mid, rootId << 1, l, r, val);
        update(mid + 1, end, rootId << 1 | 1, l, r, val);
        pushUp(rootId);
    }
    private int query(int start, int end, int l, int r, int rootId) {
    
        if (r < start || l > end) return 0;
        else if (l <= start && end <= r) return tree[rootId];
        int mid = (start + end) >> 1;
        // 下推标记
        pushDown(rootId, mid - start + 1, end - mid);
        int lSum = query(start, mid, l, r, rootId << 1);
        int rSum = query(mid + 1, end, l, r, rootId << 1 | 1);
        return lSum + rSum;
    }

    private void pushUp(int rootId) {
    
        tree[rootId] = tree[rootId << 1] + tree[rootId << 1 | 1];
    }
    private void pushDown(int rootId, int leftNum, int rightNum) {
    
        if (add[rootId] == 0) return ;
        // 下推标记
        add[rootId << 1] += add[rootId];
        add[rootId << 1 | 1] += add[rootId];
        // 修改子节点的 Sum 使之与对应的 add 相对应
        tree[rootId << 1] += leftNum * add[rootId];
        tree[rootId << 1 | 1] += rightNum * add[rootId];
        add[rootId] = 0;
    }
}

方法二：基于动态开点，完全是为了加深对动态开点的理解

class NumArray {
    

    public NumArray(int[] nums) {
    
        N = nums.length - 1;
        for (int i = 0; i <= N; i++) {
    
            update(root, 0, N, i, i, nums[i]);
        }
    }
    
    public void update(int index, int val) {
    
        update(root, 0, N, index, index, val);
    }
    
    public int sumRange(int left, int right) {
    
        return query(root, 0, N, left, right);
    }

    class Node {
    
        // 左右孩子节点
        Node left, right;
        // 当前节点值，以及懒惰标记的值
        int val, add;
    }
    private int N;
    private Node root = new Node();
    public void update(Node node, int start, int end, int l, int r, int val) {
    
        if (l <= start && end <= r) {
    
            node.val = (end - start + 1) * val;
            node.add = val;
            return ;
        }
        int mid = (start + end) >> 1;
        pushDown(node, mid - start + 1, end - mid);
        if (l <= mid) update(node.left, start, mid, l, r, val);
        if (r > mid) update(node.right, mid + 1, end, l, r, val);
        pushUp(node);
    }
    public int query(Node node, int start, int end, int l, int r) {
    
        if (l <= start && end <= r) return node.val;
        int mid = (start + end) >> 1, ans = 0;
        pushDown(node, mid - start + 1, end - mid);
        if (l <= mid) ans += query(node.left, start, mid, l, r);
        if (r > mid) ans += query(node.right, mid + 1, end, l, r);
        return ans;
    }
    private void pushUp(Node node) {
    
        node.val = node.left.val + node.right.val;
    }
    private void pushDown(Node node, int leftNum, int rightNum) {
    
        if (node.left == null) node.left = new Node();
        if (node.right == null) node.right = new Node();
        if (node.add == 0) return ;
        node.left.val = node.add * leftNum;
        node.right.val = node.add * rightNum;
        node.left.add = node.add;
        node.right.add = node.add;
        node.add = 0;
    }
}

最近的请求次数

题目详情可见 最近的请求次数

方法一：线段树 (动态开点)；完全是为了加深对线段树的理解

class RecentCounter {
    

    public RecentCounter() {
    

    }
    
    public int ping(int t) {
    
        update(root, 1, N, t, t, 1);
        return query(root, 1, N, Math.max(0, t - 3000), t);
    }

    // *************** 下面是模版 ***************
    class Node {
    
        // 左右孩子节点
        Node left, right;
        // 当前节点值，以及懒惰标记的值
        int val, add;
    }
    private int N = (int) 1e9;
    private Node root = new Node();
    public void update(Node node, int start, int end, int l, int r, int val) {
    
        if (l <= start && end <= r) {
    
            node.val += val;
            node.add += val;
            return ;
        }
        int mid = (start + end) >> 1;
        pushDown(node, mid - start + 1, end - mid);
        if (l <= mid) update(node.left, start, mid, l, r, val);
        if (r > mid) update(node.right, mid + 1, end, l, r, val);
        pushUp(node);
    }
    public int query(Node node, int start, int end, int l, int r) {
    
        if (l <= start && end <= r) return node.val;
        int mid = (start + end) >> 1, ans = 0;
        pushDown(node, mid - start + 1, end - mid);
        if (l <= mid) ans = query(node.left, start, mid, l, r);
        if (r > mid) ans += query(node.right, mid + 1, end, l, r);
        return ans;
    }
    private void pushUp(Node node) {
    
        node.val = node.left.val + node.right.val;
    }
    private void pushDown(Node node, int leftNum, int rightNum) {
    
        if (node.left == null) node.left = new Node();
        if (node.right == null) node.right = new Node();
        if (node.add == 0) return ;
        node.left.val += node.add * leftNum;
        node.right.val += node.add * rightNum;
        // 对区间进行「加减」的更新操作，下推懒惰标记时需要累加起来，不能直接覆盖
        node.left.add += node.add;
        node.right.add += node.add;
        node.add = 0;
    }
}

方法二：队列

class RecentCounter {
    

    private Deque<Integer> deque;

    public RecentCounter() {
    
        deque = new ArrayDeque<>();
    }
    
    public int ping(int t) {
    
        int past = t - 3000;
        deque.addLast(t);
        while (deque.getFirst() < past) deque.removeFirst();
        return deque.size();
    }
}

掉落的方块

题目详情可见 掉落的方块

上面说过「节点的值不止可以表示该区间的和」，还可以「表示为当前区间的最值」，该题目存储的就是区间的最大值

class Solution {
    
    public List<Integer> fallingSquares(int[][] positions) {
    
        List<Integer> ans = new ArrayList<>();
        for (int[] position : positions) {
    
            int x = position[0], h = position[1];
            // 先查询出 [x, x + h] 的值
            int cur = query(root, 0, N, x, x + h - 1);
            // 更新 [x, x + h - 1] 为 cur + h
            update(root, 0, N, x, x + h - 1, cur + h);
            ans.add(root.val);
        }
        return ans;
    }
    // *************** 下面是模版 ***************
    class Node {
    
        // 左右孩子节点
        Node left, right;
        // 当前节点值，以及懒惰标记的值
        int val, add;
    }
    private int N = (int) 1e9;
    private Node root = new Node();
    public void update(Node node, int start, int end, int l, int r, int val) {
    
        if (l <= start && end <= r) {
    
            node.val = val;
            node.add = val;
            return ;
        }
        pushDown(node);
        int mid = (start + end) >> 1;
        if (l <= mid) update(node.left, start, mid, l, r, val);
        if (r > mid) update(node.right, mid + 1, end, l, r, val);
        pushUp(node);
    }
    public int query(Node node, int start, int end, int l, int r) {
    
        if (l <= start && end <= r) return node.val;
        pushDown(node);
        int mid = (start + end) >> 1, ans = 0;
        if (l <= mid) ans = query(node.left, start, mid, l, r);
        if (r > mid) ans = Math.max(ans, query(node.right, mid + 1, end, l, r));
        return ans;
    }
    private void pushUp(Node node) {
    
        // 每个节点存的是当前区间的最大值
        node.val = Math.max(node.left.val, node.right.val);
    }
    private void pushDown(Node node) {
    
        if (node.left == null) node.left = new Node();
        if (node.right == null) node.right = new Node();
        if (node.add == 0) return ;
        node.left.val = node.add;
        node.right.val = node.add;
        node.left.add = node.add;
        node.right.add = node.add;
        node.add = 0;
    }
}