Ten thousand word summary data storage, three knowledge points

🧸🧸🧸 Hello, guys , I'm pig skin brother 🧸🧸🧸

Here is the following knowledge content 🥳🥳🥳

Preface

     What we are learning today is Data storage （ Including the byte order of the big and small ends ） The following content is very hard core , Get the bench , Today's content officially begins ！！！！

---

One 、 The significance of data storage

1. Use this type to exploit the size of memory space （ Size determines the range of use ）
2. Type determines how to view memory space

---

Two 、 Basic classification of types

1. The integer family

The integer family ：( although char Is a character type , But when character types are stored , What is stored is the of characters ASCLL Code value ,ASCLL The code value is an integer , So it is classified into integer family ), A picture is attached below to describe

in general , Is the concept of signed and unsigned

2. Floating point family

Floating point family ：
float,double,long double

3. Construction type

Construction type ( Custom type , Create it yourself )
· An array type
· Type of structure struct
· Enumeration type enum
· Joint type union

4. Pointer types

5. Empty type

Empty type （ That is to say void type , Also called no type ）
void test(void)// Unwanted parameter when , It can be written. void, Or not
One kind of pointer is void* Pointer to type

---

3、 ... and 、 Integer promotion and arithmetic conversion （ The following calculation will use ）!!!

1. Implicit type conversion

Concept ：
C Integer arithmetic operations are always performed at least with the precision of the default integer type .
To get this accuracy , Characters and short operands in expressions are converted to normal integers before use , This conversion is called integer promotion .

2. The significance of integer Promotion

     The integer operation of expression should be in CPU In the corresponding computing device of ,CPU Inner integer arithmetic unit ALU The byte length of the operands of is generally int Byte length of , It's also CPU The length of the general register of .
therefore , Even two char The addition of types , stay CPU When executing, it should be converted to CPU The standard length of the inner operands .( That is to say int)
Various lengths in expressions may be less than int The integer value of the length , Must be converted to int or unsigned int, Then it can be sent in CPU To perform the operation

3. Calculation of integer lift

Unsigned numbers are unsigned Number of types , It is related to signed numbers signed Type comparison , The highest bit is not the sign bit , It is also used to calculate the data size
such as

When integer lifting , If the highest level is 1 Then fill 1, If the highest level is 0, Then fill 0;
Anything less than an integer is converted to int or unsigned int
And then I'll take part in the calculation

example 1
char a=-1;
10000000 00000000 00000000 00000001//-1 The original code of
11111111 11111111 111111111 11111111//-1 Complement
11111111    int type —>char type ( Truncation occurred )
printf(“%d”,a);, because %d It is printed with signed integer , So we need to int type ,char The type is only one byte in size , Not enough , So integer promotion occurs
11111111 11111111 11111111 11111111 Plastic lifting occurs
char a=-1;
10000000 00000000 00000000 00000001//-1 The original code of
11111111 11111111 111111111 11111111//-1 Complement
11111111    int type —>char type ( Truncation occurred )
printf(“%d”,a);, because %d It is printed with signed integer , So we need to int type ,char The type is only one byte in size , Not enough , So integer promotion occurs
11111111 11111111 11111111 11111111 Plastic lifting occurs

Example 2
char a=5
Deposit is 00000101（ The first bit is the sign bit ）
char b=126
Deposit is 01111110（ The first bit is the sign bit ）
char c=a+b;
00000101
01111110
Cannot reach an integer when adding , Plastic lifting will occur
00000000 00000000 00000000 00000101-a
00000000 00000000 00000000 011111110-b
00000000 00000000 00000000 10000011
Re truncation
10000011-c
11111111 11111111 1111111 10000011
1000000 0000000 0000000 01111101-c The original code of （ The sign bits remain the same , Other bits are reversed ）
So get -125

4. Arithmetic conversion

Arithmetic conversion is the conversion of data types with small bytes to data types with large bytes

---

Four 、 The storage of integers in memory

     The first First , The data stored in the computer is binary , Different types only exist in different ways .

There are three representations of integers in computers ： Original code 、 Inverse code 、 Complement code
Pay attention , Integer. , Floating point type does not say the original inverse complement

Original code 、 Inverse code 、 Complement code

① The conversion method of positive and negative number original inverse complement

Integer stores complement in memory
There are three representations Sign bit and The number Two parts

The calculation method is as follows ：
1. The original code of positive numbers and the complement of negative numbers are the same
2. Negative amount original code , Inverse code , Complement is expressed in different ways
     The inverse code of a negative number is equal to the inverse of the original code by bits except for the sign bit
     Then on the basis of inverse code , add 1 You get the complement of the negative number
3. A negative complement -----> Original code
     You can first add the complement of a negative number -1 Then, in addition to the sign bit, the bit is reversed
     You can also reverse the complement of a negative number, except for the sign bit, and then 1

Case diagram ：

The representation of data

② Why is data stored in the form of complement

In computer system , All values are represented by complements
The reason lies in ：
Use complement , Symbol bits and value fields can be treated in a unified way
meanwhile , Addition and subtraction can also be handled in a unified way （CPU There is only an adder ）, In addition, the complement code and the original code are converted to each other , Its operation process is the same , No need for additional hardware circuits

Here is an example to illustrate CPU There is no subtracter in
Case diagram ：

And if the memory is 1000… A pile of zeros in the back
        such as char Type of 10000000 ( Complement code ), He has nothing to reduce , It will be directly parsed into -128, This is very important

③ Take a few examples

One 、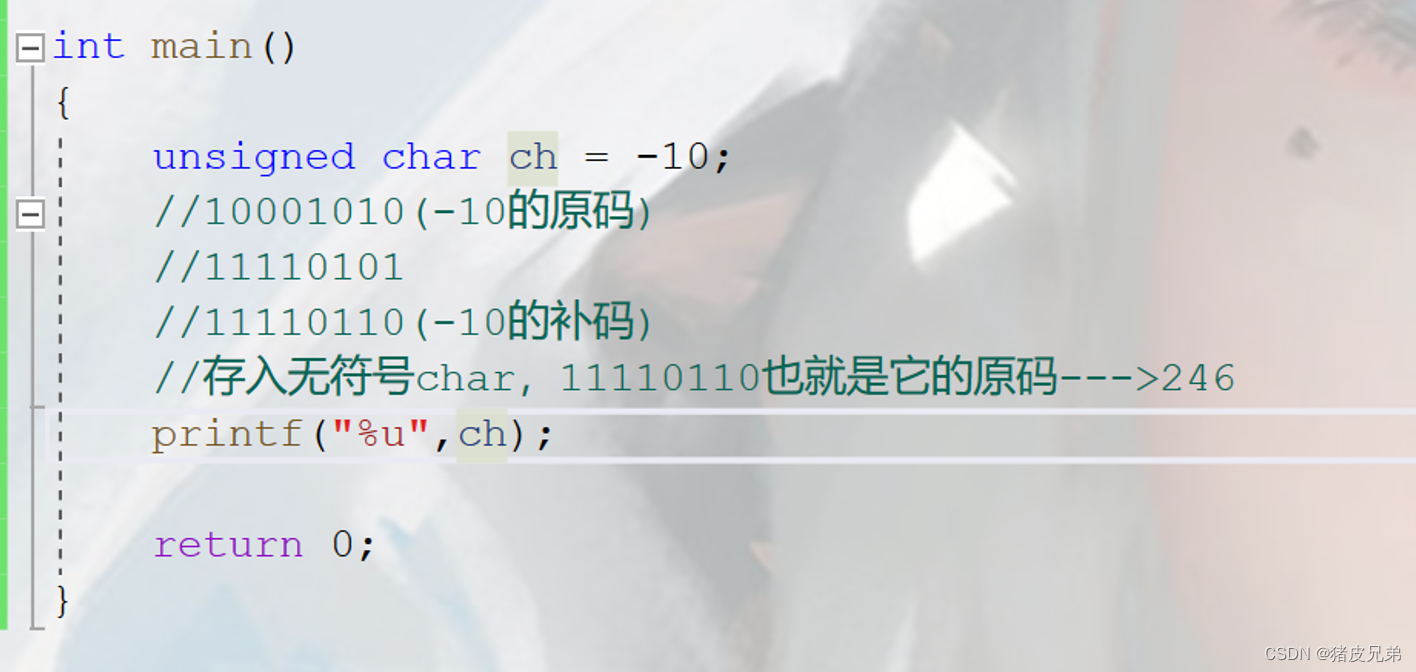

Print the value of unsigned number with %u
%u Is to print unsigned numbers , What you want me to print must be an unsigned number , It's not an unsigned number. I also think it's an unsigned number
%d It is printed with signed numbers , What you want me to print must be a signed number , It's not a signed number. I also think it's a signed number
however unsigned int ch=-10;
Have already put ch The assignment is positive （ because ch The type is unsigned char）; So I use %d and %u It doesn't matter to print

But this won't work anymore

Another example ：（ Integer lifting has been mentioned above ）

int main()
{
    
	char a = -128;
	//-128 Complement code 11111111 11111111 11111111 10000000
	// Deposit in a Truncation occurred in  10000000

	// To have an integer lift / Because the high position is 1, So make up 1
	//11111111 11111111 11111111 10000000
	printf("%u",a);
	return 0;
}

int main()
//{
    
	int i = -20;
	10000000 00000000 00000000 00010100
	11111111 11111111 11111111 11101011
	11111111 11111111 11111111 11101100
	unsigned int j = 10;
	00000000 00000000 00000000 00001010
	printf("%d\n",i+j);
	11111111 11111111 11111111 11110110
	10000000 00000000 00000000 00001010
	// result -10
	return 0;
}

about char Type of storage , Knowing this, you can do the following problem

// subject 1
#include <string.h>
int main()
{
    
	char a[1000];
	int i;
	for (i = 0; i < 1000; i++)
	{
    
		a[i] = -1 - i;
	}
	printf("%d",strlen(a));
	//255( Because I met 0 It's over , So one is missing , No 256)
	return 0;
}
// subject 2
unsigned char i = 0;
int main()
{
    
	for (i = 0; i <= 255; i++)
	{
    
		// because i The value of 0-255 In between , So the result is an endless cycle 

		printf("hello world\n");
	}
	return 0;
}

Here we are. , The storage of integers in the computer is over , Have a cup of tea , Next , We continue to study the storage of floating-point numbers in computers

---

5、 ... and 、 Storage of floating-point numbers in memory

Common floating point numbers ：
3.14159
1E10// This is the scientific notation of floating point numbers , That is to say 1.0*10^10
The floating-point family includes float,double ,long double
The range represented by floating-point numbers is float.h As defined in

1. The difference between the storage of integers and floating-point numbers in memory

Take a look at the following code , What do you think its value is

int main()
{
    
	int n = 9;
	float* pFloat = (float*)&n;//int*
	printf("n The value of is :%d\n",n);
	printf("*pFloat The value of is :%f\n", *pFloat);
	*pFloat = 9.0;
	printf("n The value of is :%d\n", n);
	printf("*pFloat The value of is :%f\n", *pFloat);
	return 0;
}

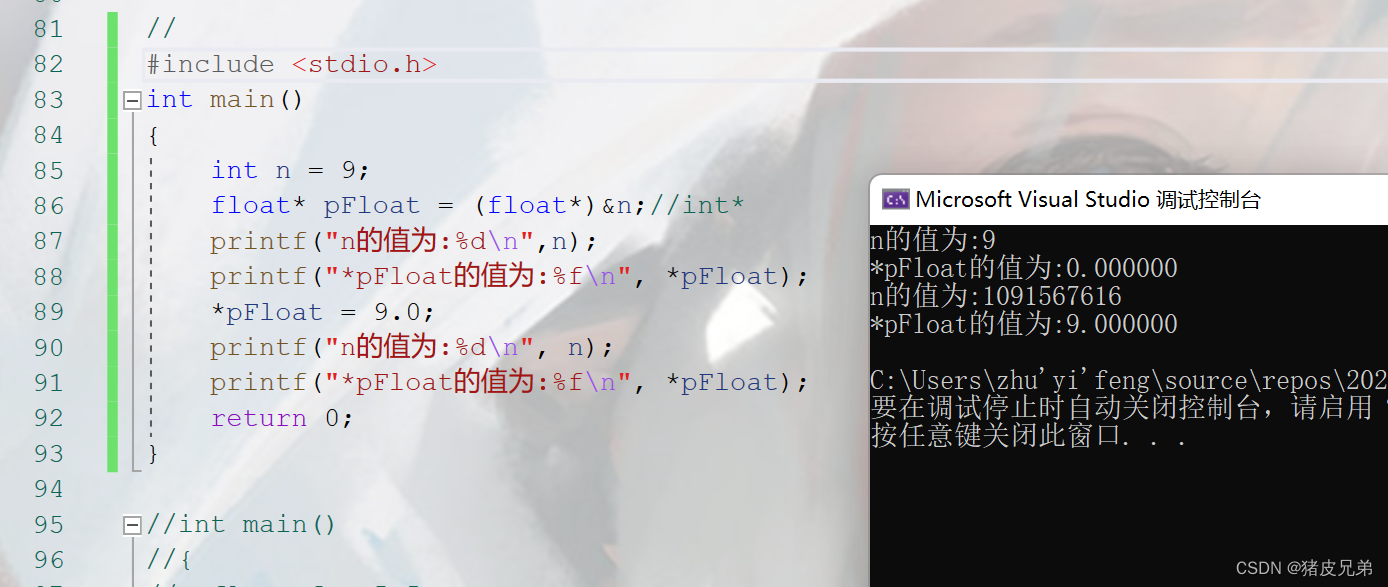
Is the result the same as what you think ？

float a=5.5;
5.5 Binary is not 101.101, So how much should it equal ？
We know , Binary system 111 Each one represents
1x(2^1) 、1x(2^1) 、 1x(2^0)
that ,0.5 Namely 1x(2^-1)
therefore ,5.5 Binary of is actually 101.1
Expressed by scientific counting , Namely 1.001 * 2^2
Plus the sign bit, it is (-1)^0 * 1.001 * 2^2

that 9.0 How to express ？

that 3.14 Well ？
3.14 Binary storage of is actually
11.00000…（ There are many in the back 0 or 1）, The purpose is to make him as close as possible 3.14
therefore , It can be seen from this that many floating-point numbers cannot be accurately saved in computers

therefore , You can't compare with floating-point numbers , You can only subtract a value from a floating-point number , Judge whether the result is within the error range specified by you

2. Floating point storage

IEEE 754 Regulations
SME
about 32 Floating point number of bits , The highest 1 Bits are sign bits S, And then 8 Bits are exponents E, The rest 23 Bits are significant numbers M
about 64 Floating point number of bits , The highest 1 Bits are sign bits S, And then 11 Bits are exponents E, The rest 52 Bits are significant numbers M

Because when stored inside the computer , By default, the first digit of this number is always 1, So it can be discarded , Save only the back xxxxx part . For example preservation 1.01 when , Save only 01, This can save a bit of space , Make it more accurate

For index E
First ,E For an unsigned integer
It means , If E by 8 position , So the scope is 0-255, If E by 11 position , So the scope is 0-2047
however , We know E Can be negative , Like the example above
therefore IEEE 754 It also stipulates that
In memory E The true value of must be added with an intermediate number , about 8 Bit E, The middle number is 127; To and 11 Is it 1023
That is to say, save -1 Add 127 perhaps 1023, The same is true when adding positive numbers
The purpose is to make negative numbers become positive numbers

int main()
{
    
	float f = 5.5;
	101.1
	(-1)^0*1.011*2^2
	S=0;//S It's a sign bit 
	E=2;   2+127=129 10000001// E Occupied 8 individual bit It's an unsigned integer 
	M=1.011
	 Store it in memory ;
	0 10000001 01100000000000000000000//M preservation 011, Back up 0
	 Into hexadecimal 
	0100 0000 1011 0000 0000 0000 0000 0000
	 The result should be 0x40b00000
	return 0;
}

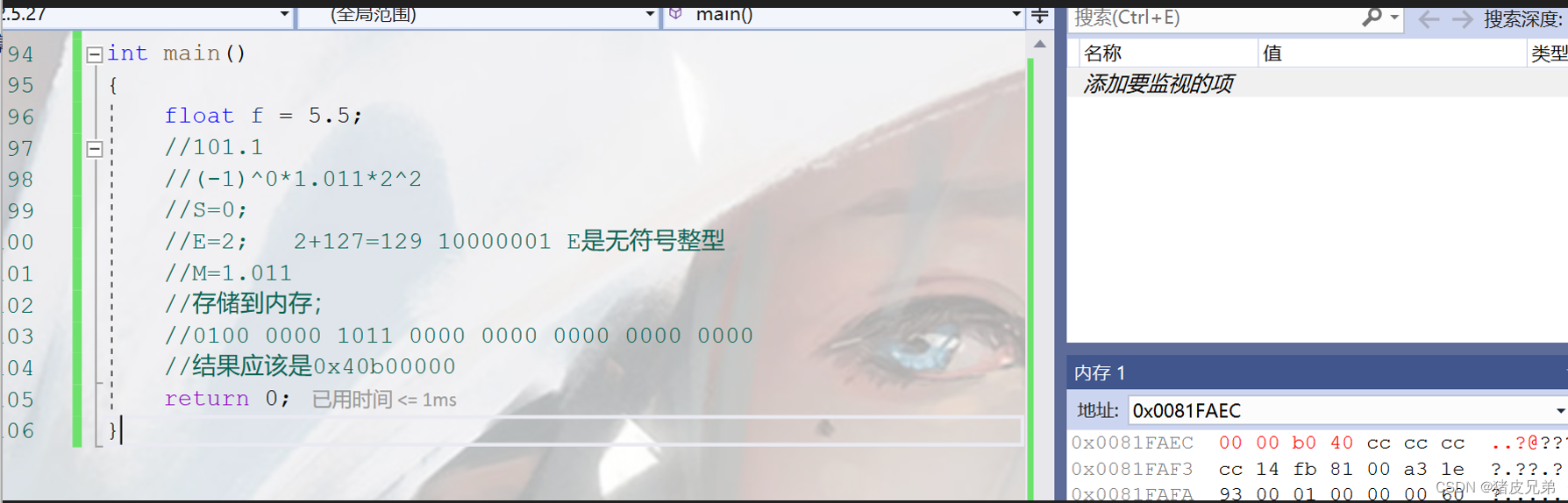
The address here involves the problem of size , The following will explain

Index E There are also three cases of fetching from memory
E Not all for 0 Or not all of them 1
then -127 or -1023 Get the real value （ Because I added 127 perhaps 1023）
E For all 0
At this time ,1-127（ perhaps 1-1023） Is the real value
Significant figures are no longer added to the preceding 1, Directly restore to 0.xxxxxx Decimals of , This is to show that ±0, So as to approach 0 A very small number of
E For all 1
At this time , If the significant number M All for 0, Express ±∞（ It depends on the sign bit S）

int main()
{
    
	int n = 9;
	00000000 00000000 00000000 00001001
	// Floating point numbers are thought to be 
	0 00000000 00000000000000000001001
	 Consider true 
	E yes 1-127 -> -126
	M yes 0.00000000000000000001001
	S yes 0
	(-1)^0 * 0.00000000000000000001001 * 2(-126) ->0.000000
	float* pFloat = (float*)&n;
	printf("n The value of is :%d\n",n);
	printf("*pFloat The value of is :%f\n", *pFloat);
	*pFloat = 9.0;//1001.0
	S=0,M=1.001, E=3  (3+127 Put into )
	0 10000010 00100000000000000000000
	%f Printing is 9.000000
	 use %d Print what he thinks is a big integer 
	printf("n The value of is :%d\n", n);
	printf("*pFloat The value of is :%f\n", *pFloat);
	return 0;
}

6、 ... and 、 Byte order at the large and small end

1. The concept of byte order storage at the large and small ends

The left side of the data is high , The right is low

The concept of byte order storage at the large and small ends
1. Big end byte order storage ： Store the data at the lower byte of a data in the high address , Store the data at the high byte at the low address .
2. Small end byte order storage ： Store the data at the lower byte of a data in the high address , Store the data at the high byte at the low address .

2. Why is there a large and small byte order

Because in the computer system , We are in bytes , Each address corresponds to a byte . A byte is 8 individual bit, But in C In language , except 8bit Of char Outside , also 16bit Of short,32bit Of long,int these .
For digits greater than 8bit The processor of , for example 16 Bit or 32 Bit processor , Because the width of the register is greater than one byte , So there must be a problem of how to arrange multiple bytes . Therefore, it leads to the emergence of large and small end mode

3. Simple judgment of byte order at the big and small ends

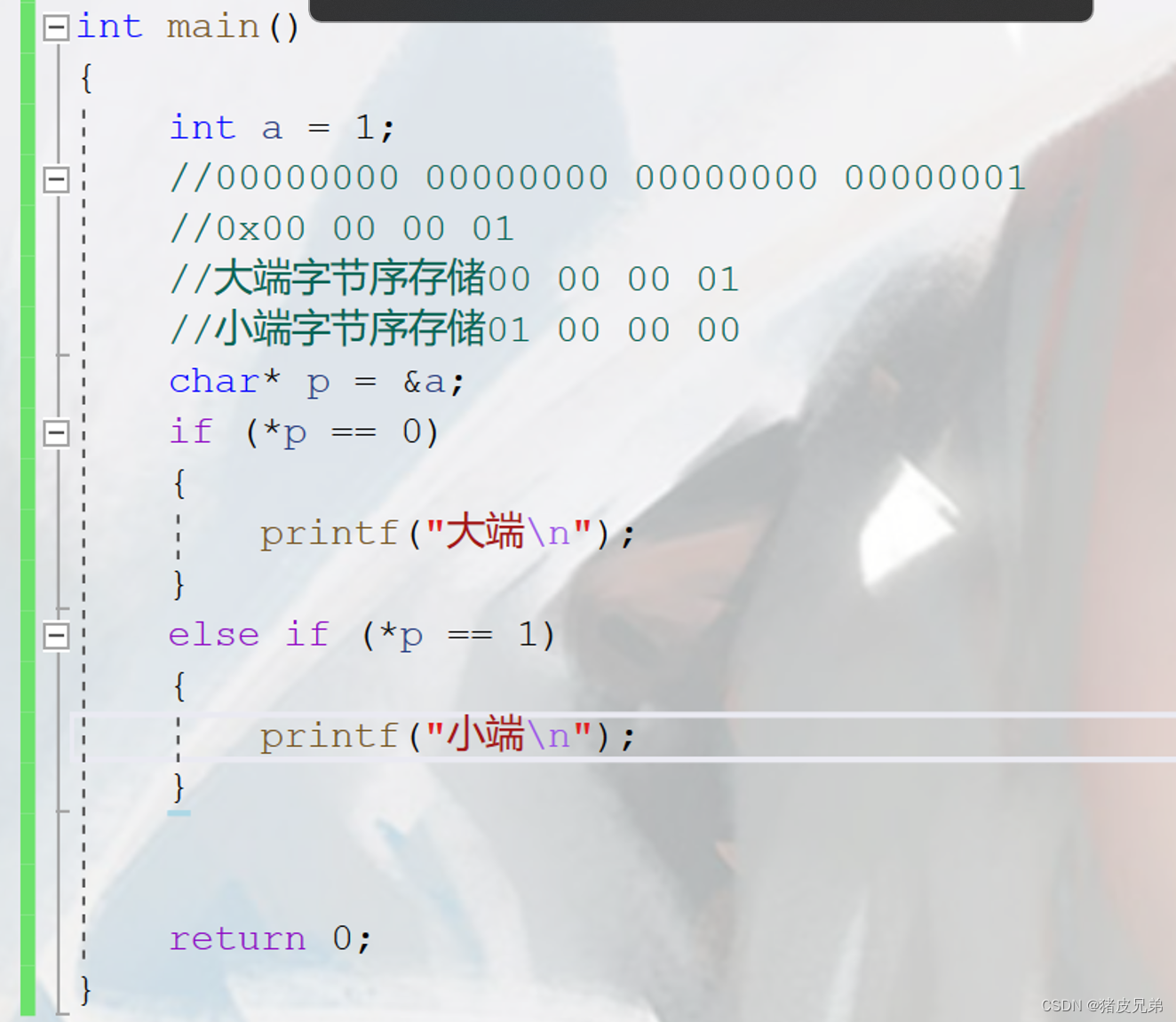
Okay , That's all for today's minesweeping game , Thank you for your support for pigskin ！！！

---

7、 ... and 、 5、 ... and The color spot Beautiful Of One some Scrap word

        When you see here , I believe the above content has been memorized ‍️‍️‍️. Guys, if you think it's helpful , I also hope you folks can use your little hands to give advice . Is there a problem with one button three times ？ No problem , What are these ？ traditional code of conduct