当前位置:网站首页>数据分析——seaborn可视化(笔记自用)
数据分析——seaborn可视化(笔记自用)
2022-07-06 03:18:00 【七上八下的黑】
参考内容
【Python】一小时带你掌握seaborn可视化_哔哩哔哩_bilibili
目录
3、figure-level functions具有FacetGrid特性
4、sns.jointplot():绘制两个变量的联合分布和各自分布
(2)jointplot的升级版:JointGrid,可通过g.plot自定义函数
(3)sns.pairplot():成对绘制所有数值变量的联合分布
(4)pairplot的升级版:PairGrid,可通过g.map自定义函数
(5)data.corr()+sns.heatmap():成对绘制所有数值变量的相关系数
1、类别变量的分布:sns.countplot(),类似sns.histplot()
(1)不同类别中数值变量的均值/中值估计:barplot, pointplot
(2)不同类别中数值变量的取值范围:boxplot, boxenplot
(3)不同类别中数值变量的分布图:stripplot, swarmplot, violinplot
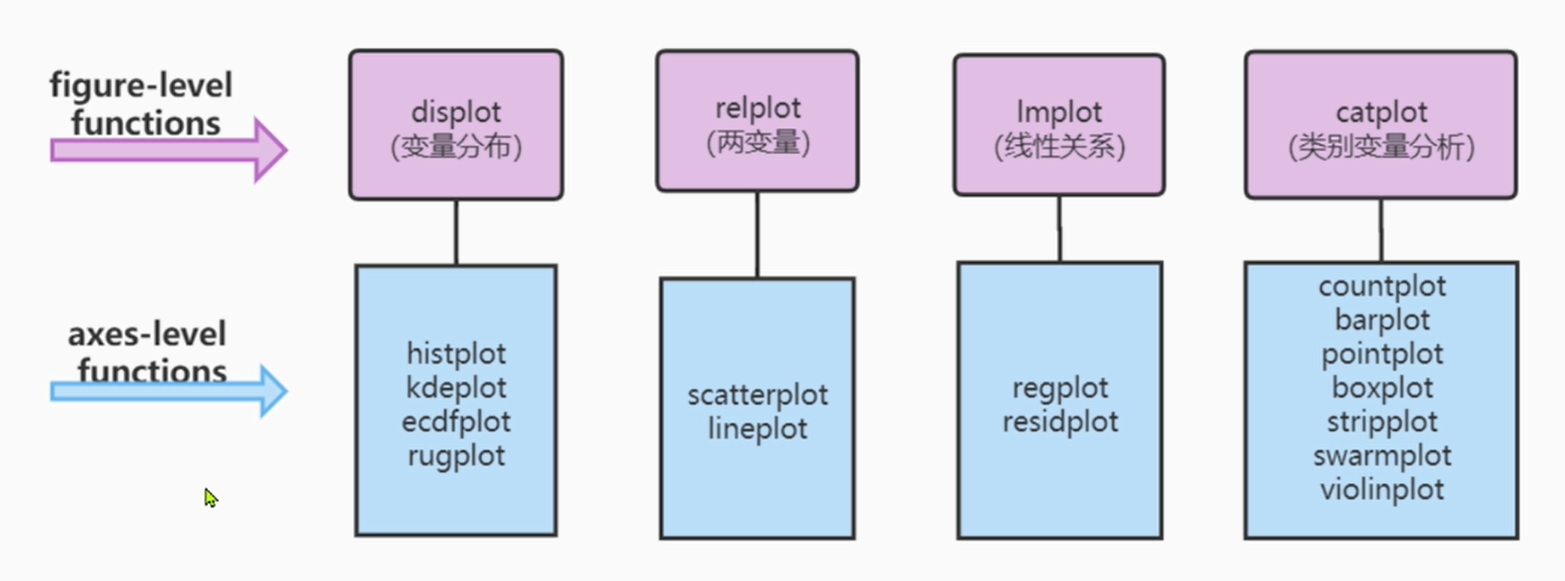
seaborn的函数结构通常可按照上图划分为:图绘制函数(紫红色)和轴绘制函数(天蓝色)。
每一类图绘制函数聚合了对应的轴绘制函数的功能,还提供相应的接口。
一、变量分布
拿到一个数据,首先要查看变量的分布:
- 变量取值范围,是否有异常值(outliers)?
- 变量分布是否近似正态分布?如果不是,那么是否有偏移?是否有双峰分布(bimodality)?
- 如果依据类别变量对数据集进行划分,各子集上变量的分布是否有很大的差异?
1、查看异常值
(1)用seaborn中自带的数据集
print(sns.get_dataset_names())
penguin_df = sns.load_dataset('penguins')
penguin_df
(2)sns.boxplot():查看数值变量的取值范围,观察是否有异常值(箱型图)
sns.boxplot(data=penguin_df, x='bill_length_mm') # 定义数据和变量名 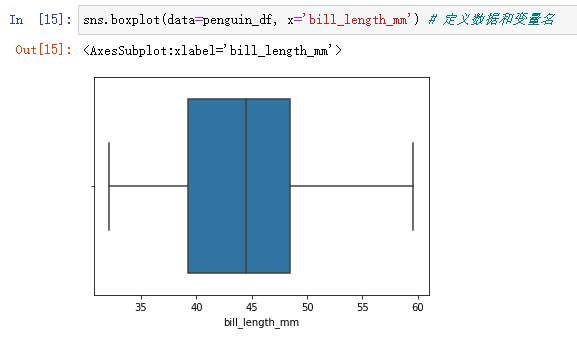
图中 箱子中间的线是数据的中值;箱体左右两个边界是四分位数(75%的值是小于49的,25%的值小于39);箱体外的两条线是表示合理范围内的最大值和最小值(用公式计算出来的),超出这个范围的话,数据就是不合理的,有可能是异常值,需要具体情况具体分析。
1、boxplot对应catplot(类别变量分析),因此箱体图也可以用catplot绘制:
sns.catplot(data=penguin_df, x='bill_length_mm',kind='box') # 需要定义kind
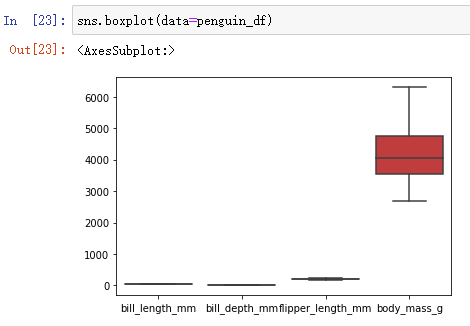
2、也可以将所有变量的箱型图放到一个图中,但往往会因为数据不是一个数量级而效果不好:
sns.boxplot(data=penguin_df)
(3)观察异常值情况
sns.boxplot(data=tip_df)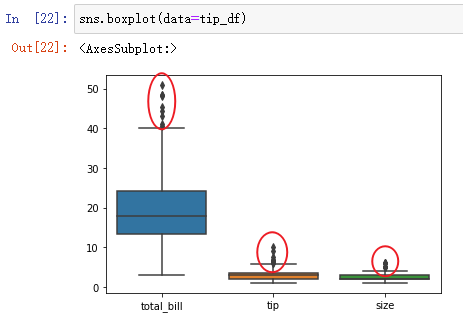
图中红色圈的部分可能是异常值的点(具体问题具体分析)。
2、观察变量分布
(1)sns.displot():查看变量的分布
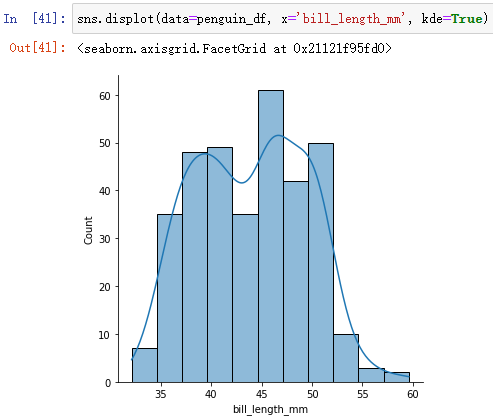
sns.displot(data=penguin_df, x='bill_length_mm') 
# 通过设置bins来控制直方图的划分
sns.displot(data=penguin_df, x='bill_length_mm', bins=50)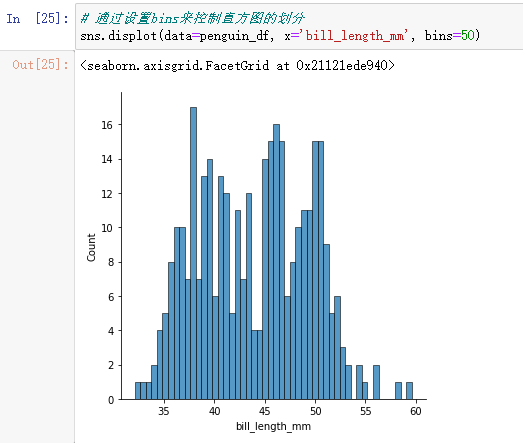
bins划分过粗可能会忽略数据的分布特征,但有时划分过细又会导致过分解读。可以看到上图呈现双峰分布。
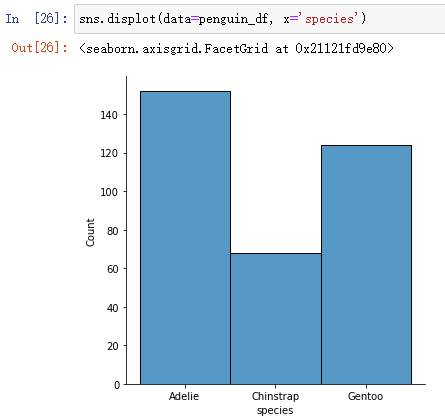
1、displot也可以对类别变量进行分析:
sns.displot(data=penguin_df, x='species')
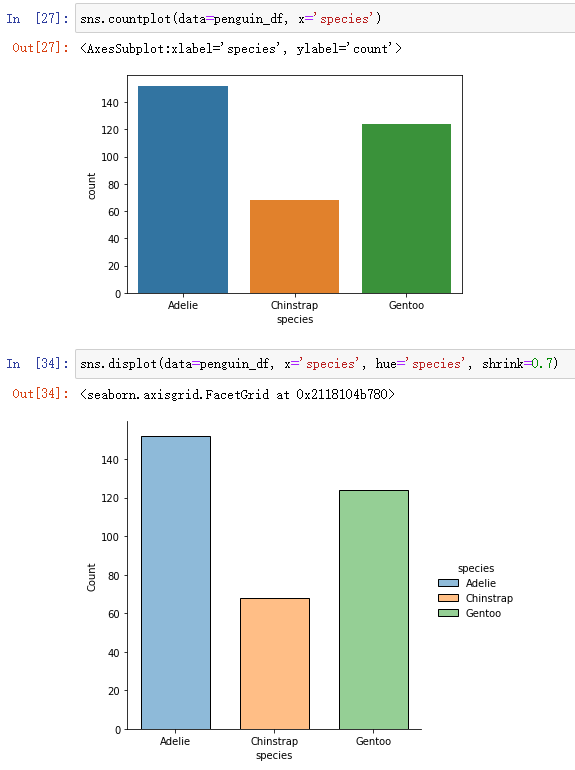
2、对比用countplot对类别变量进行分析:
sns.countplot(data=penguin_df, x='species')sns.displot(data=penguin_df, x='species', hue='species', shrink=0.7)displot可以通过hue参数进行颜色区分,通过shink对柱状图进行放缩
(2)sns.displot():看kde曲线
用核函数对数据的分布进行拟合,默认使用高斯核函数.
- 方法一:
sns.displot(data=penguin_df, x='bill_length_mm', kind='kde')- 方法二:
sns.kdeplot(data=penguin_df, x='bill_length_mm')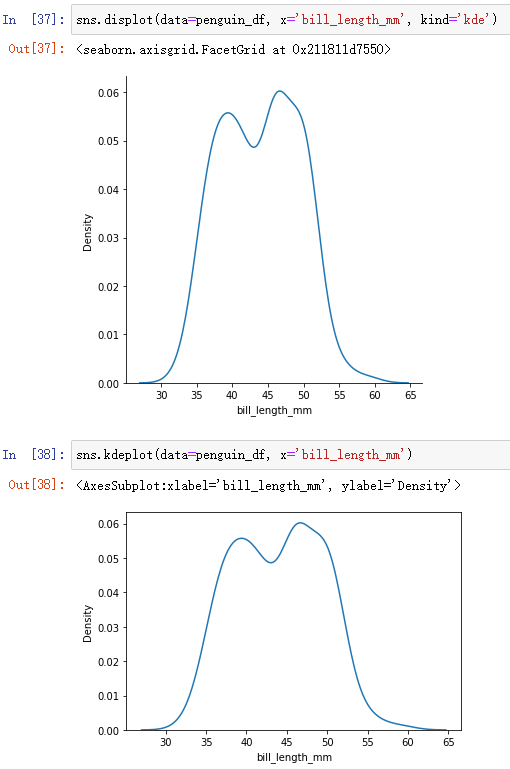
rugplot是不占空间的,可以直接叠加在displot的图像上:
sns.displot(data=penguin_df, x='bill_length_mm', kind='kde', rug=True) 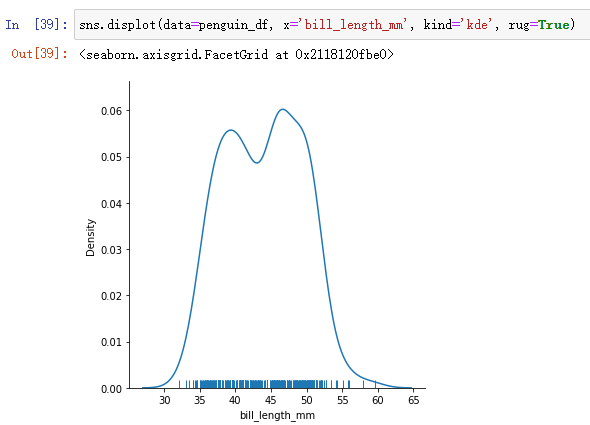
虽然kde曲线更容易观察数据的分布规律,但可能在图像边缘部分的绘制超出取值范围。
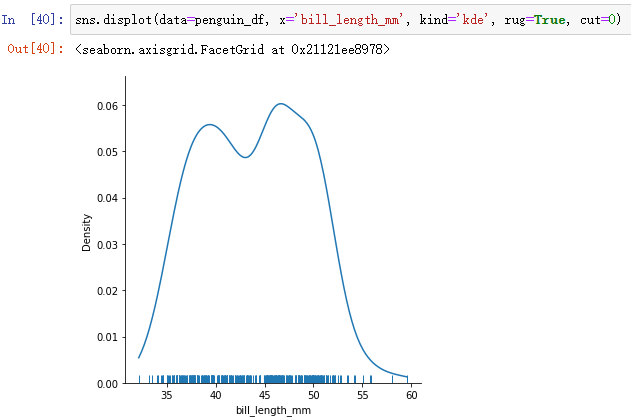
- 解决方案一:(令cut=0)
sns.displot(data=penguin_df, x='bill_length_mm', kind='kde', rug=True, cut=0)
但是这种方法可能会改变数据分布。
- 解决方案二:(在直方图上叠加绘制kde)
sns.displot(data=penguin_df, x='bill_length_mm', kde=True)
(3)分析双峰分布
sns.displot(data=penguin_df, x='bill_length_mm', kind='kde', hue='species')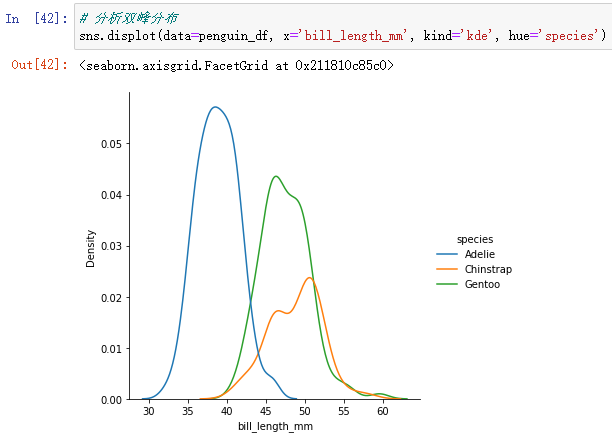
从图中可以看到,企鹅的最长在不同的种类上的kde分布是不一样的,它们之间有一定的差距。所以叠加起来会呈现双峰分布的特点。
(4)分析偏移情况
可以对数据进行对数处理
(5)经验分布函数(acdfplot)
sns.displot(data=penguin_df, x='bill_length_mm', kind='ecdf') 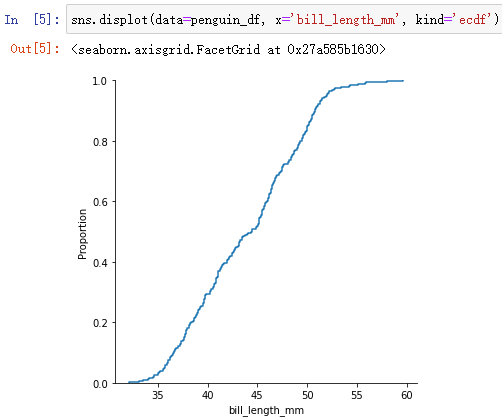
图中55对应的比例是0.97,表示数据中低于55的数据占75%。功能与箱型图比较类似,只是用不同的形式表现出来了。
3、figure-level functions具有FacetGrid特性
FacetGrid将行和列设置成类别变量,根据数据变量的不同类别,将数据划分成不同的子集,在各个子集上分析各个变量的分布。(相当于绘制了变量的条件概率分布)
sns.displot(data=penguin_df, x='bill_length_mm', row='sex', col='island', kind='kde', hue='species')将行设置为性别(有两个类别),列设置为岛屿(有三个类别),绘制企鹅的嘴长的kde曲线(bill_length_mm)。
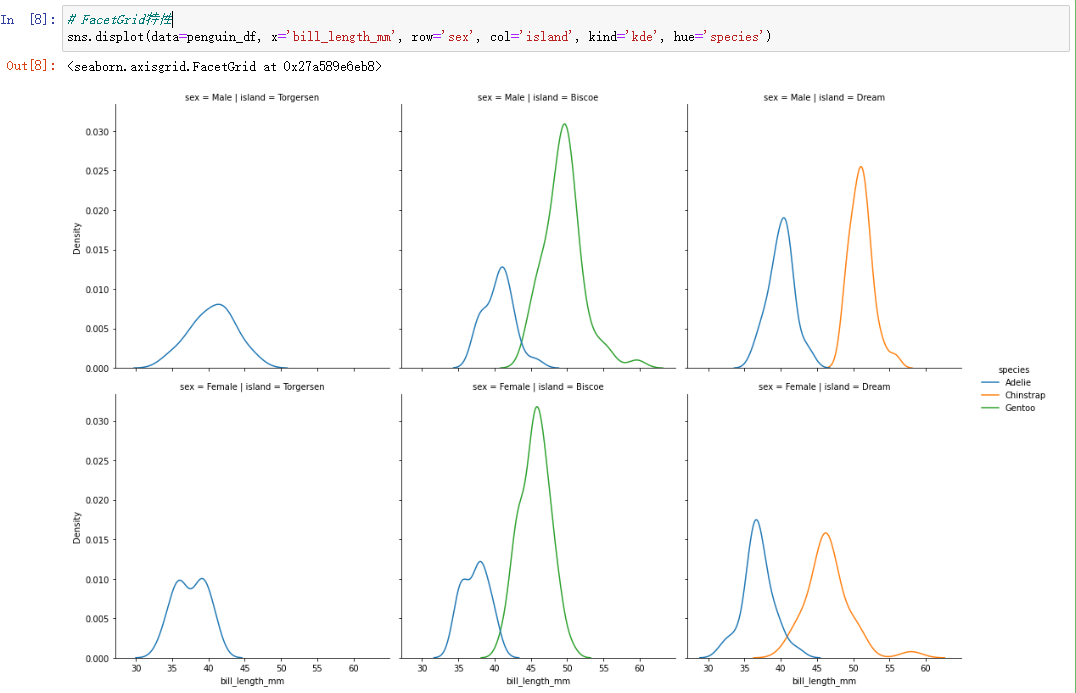
二、数值变量的关系分析
1、sns.relplot():
- 绘制散点图
sns.relplot(data=tip_df, x='total_bill', y='tip', hue='time', style='time', markers=['o', '^'])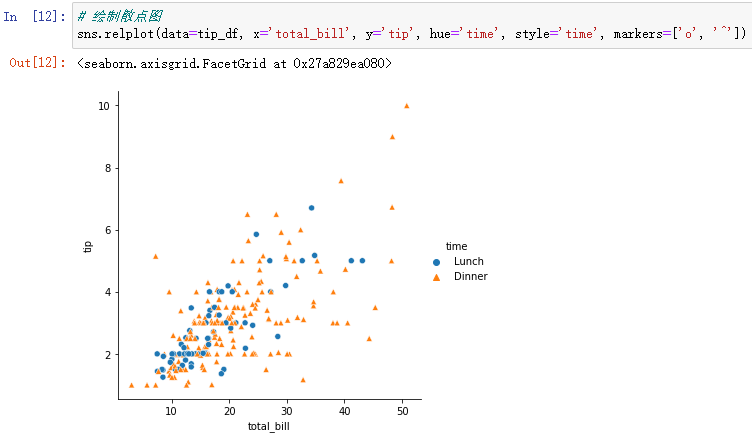
markers可以自定义图中点的样式
sns.relplot(data=tip_df, x='total_bill', y='tip', hue='size', size='size') 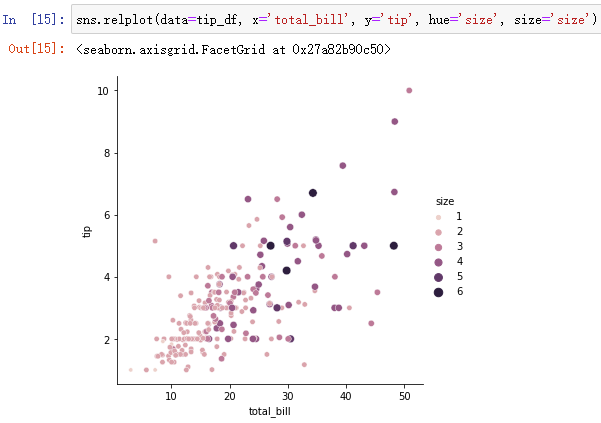
当类别较多时,会采用渐进色表示,通过size还可以设置大小。
- 绘制连线图
sns.relplot(data=tip_df, x='total_bill', y='tip',kind='line') 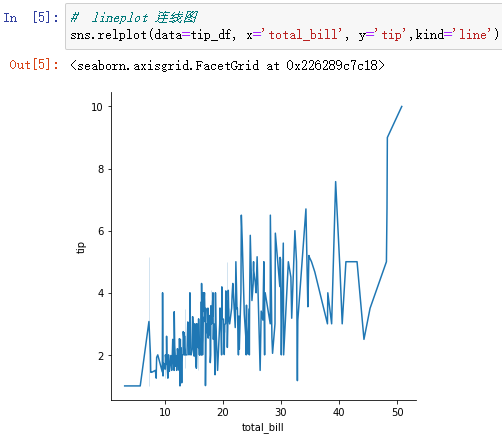
上面的图有点乱,因为连线图适合分析时序数据、股价的波动等等。
# 股价分析
stock_df = pd.DataFrame(dict(time=np.arange(500), price=np.random.randn(500).cumsum()+np.ones(500)*50))
sns.relplot(data=stock_df, x='time', y='price', kind='line') 随机数产生500个数,用累计和函数(cumsum)达到连续变化的效果来模拟股价变化。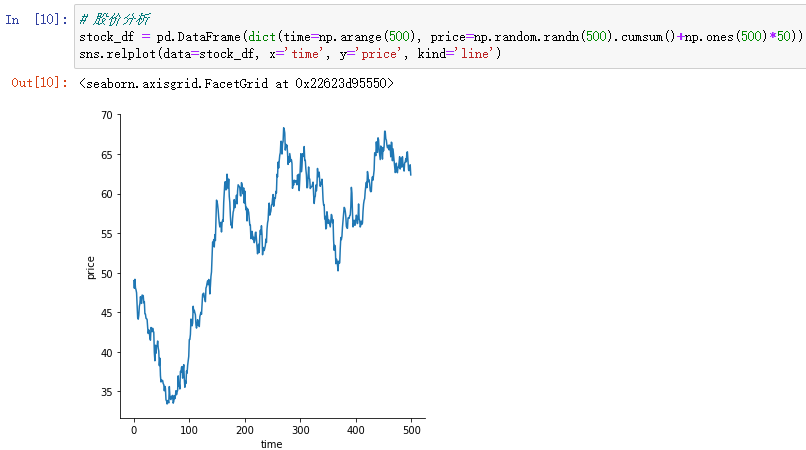
2、sns.lmplot():分析两个变量的线性关系
前面对tip_df绘制散点图时可以看到数据具有一定的相关性,因此可以用lmplot 取绘制回归线。
sns.lmplot(data=tip_df, x='total_bill', y='tip') 
regplot和lmplot 绘制回归线的效果一样:
sns.regplot(data=tip_df, x='total_bill', y='tip') 
通过residplot绘制残差图:
sns.residplot(data=tip_df, x='total_bill', y='tip') 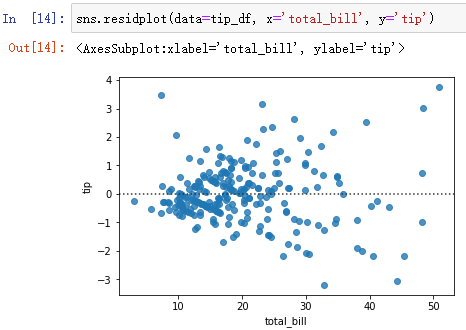
理性情况下(拟合好的话),残差应该是随机分布的,而这里的残差还呈现一定的发散分布,肯定是两个变量之间的关系还没挖掘出来。
- lmplot也可以和relplot一样添加类别变量
sns.lmplot(data=tip_df, x='total_bill', y='tip', hue='time')
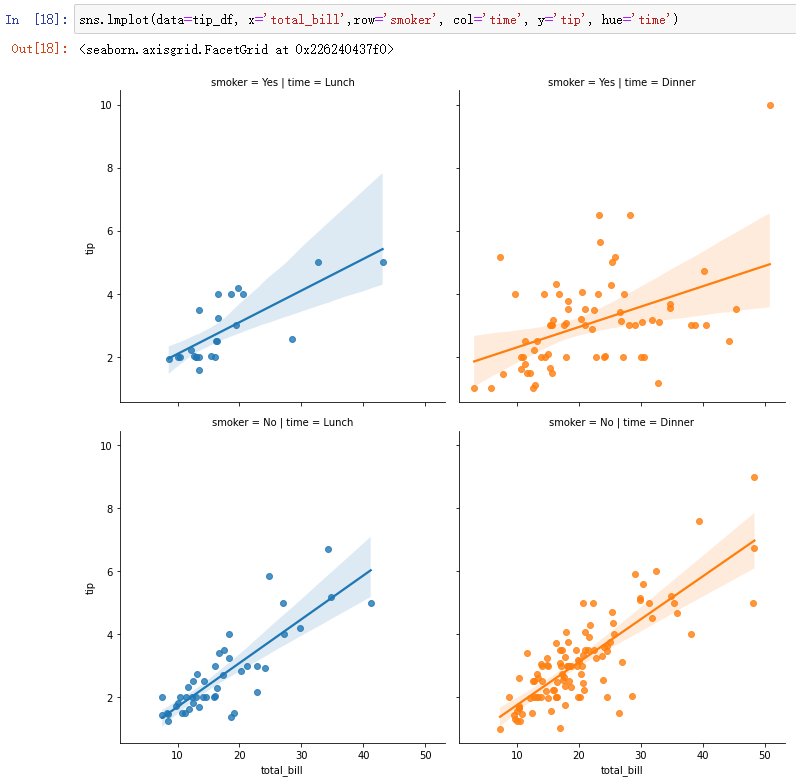
- lmplot也具有FacetGrid特性
sns.lmplot(data=tip_df, x='total_bill',row='smoker', col='time', y='tip', hue='time')
3、sns.displot():绘制两个变量的联合分布
直方图形式:
sns.displot(data=penguin_df, x='bill_length_mm', y='bill_depth_mm')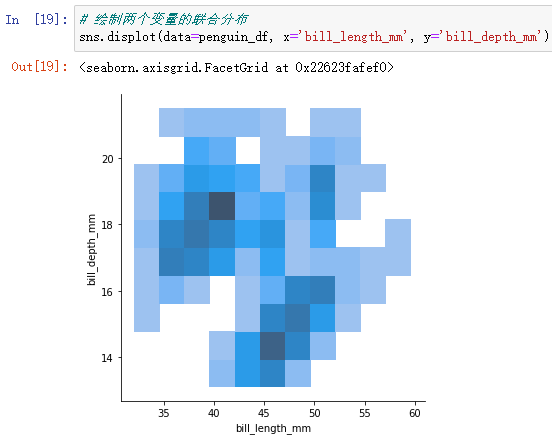
kde曲线形式:
sns.displot(data=penguin_df, x='bill_length_mm', y='bill_depth_mm', kind='kde')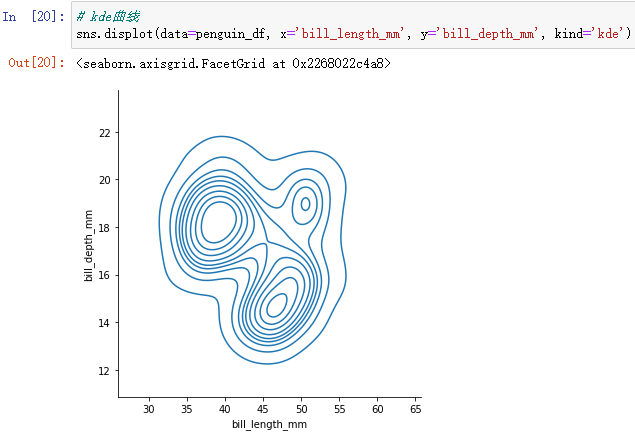
可以通过设置thresh(0-1)来控制图形显示的范围、level控制线的疏密程度。
也可以用displot绘制类别变量的联合分布:
sns.displot(data=penguin_df, x='island', y='species')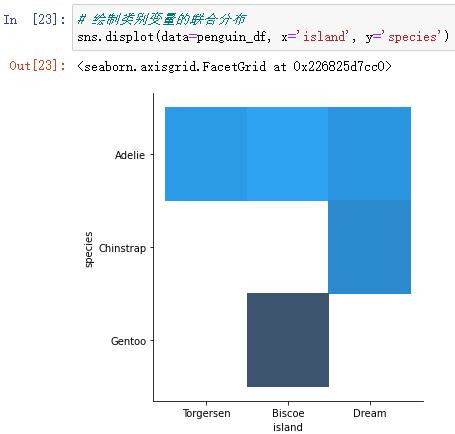
从图中可以看到,Gentoo只在Biscore island上,在Biscore island上,Gentoo占大多数,但还是有一部分的Adelie。
4、sns.jointplot():绘制两个变量的联合分布和各自分布
(1)sns.jointplot()
默认情况下,联合分布是散点图,可以通过kind进行设置。`kind` is one of ['scatter', 'hist', 'hex', 'kde', 'reg', 'resid']
sns.jointplot(data=tip_df, x='total_bill', y='tip') 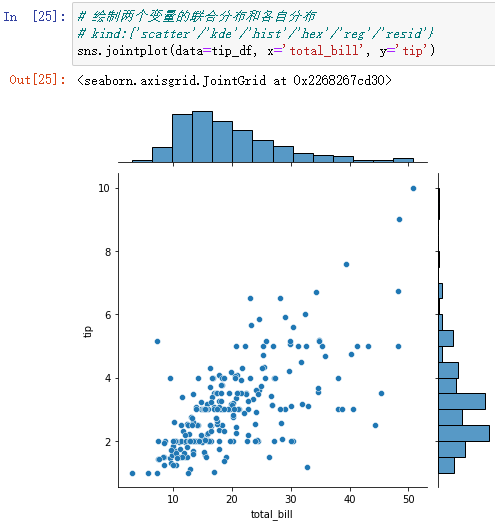
还可以通过hue加入一个类别变量:
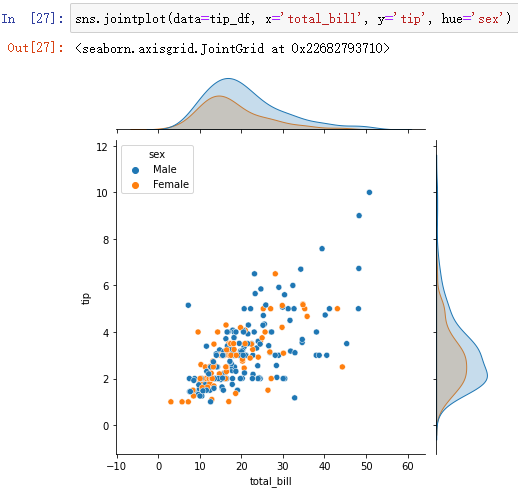
与displot相同,jointplot也可以绘制两个类别变量。
(2)jointplot的升级版:JointGrid,可通过g.plot自定义函数
g = sns.JointGrid(data=tip_df, x='total_bill', y='tip')
g.plot(sns.histplot, sns.boxplot) # 中间用直方图,边缘用箱型图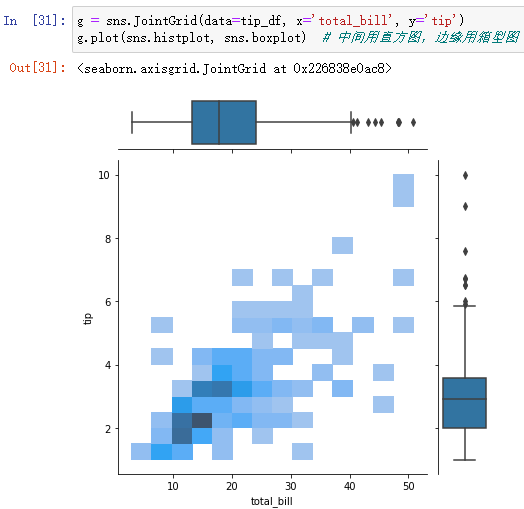
自定义部分也可以更加具体:
g = sns.JointGrid(data=tip_df, x='total_bill', y='tip')
g.plot_joint(sns.kdeplot) # 联合分布
g.plot_marginals(sns.histplot, kde=True) # 边缘各自的分布
(3)sns.pairplot():成对绘制所有数值变量的联合分布
sns.pairplot(data=tip_df, kind='kde')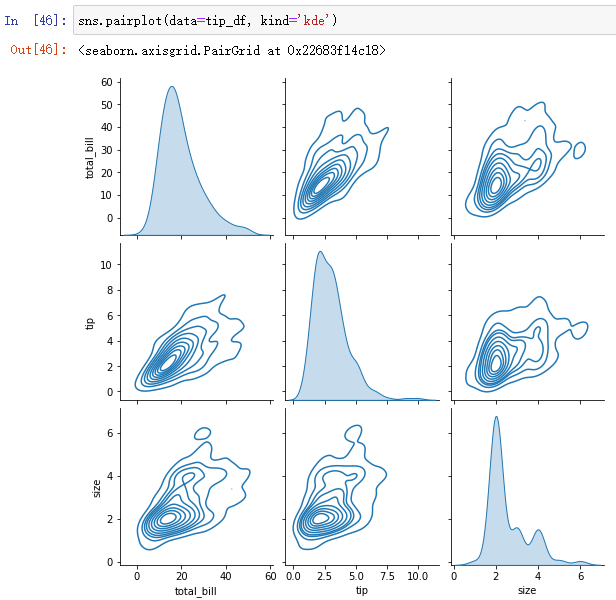
当变量较多时,可以选择自己所需的关键变量进行分析: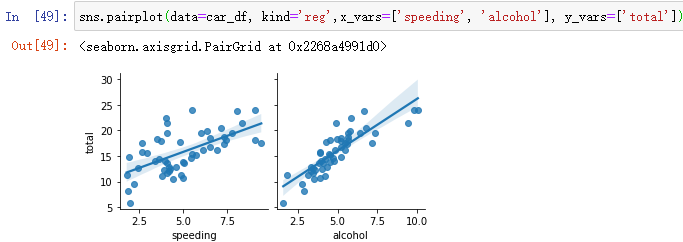
(4)pairplot的升级版:PairGrid,可通过g.map自定义函数
g = sns.PairGrid(data=car_df, x_vars=['total', 'speeding', 'alcohol'], y_vars=['total', 'speeding', 'alcohol'])
g.map_upper(sns.scatterplot)
g.map_diag(sns.histplot, kde=True)
g.map_lower(sns.regplot)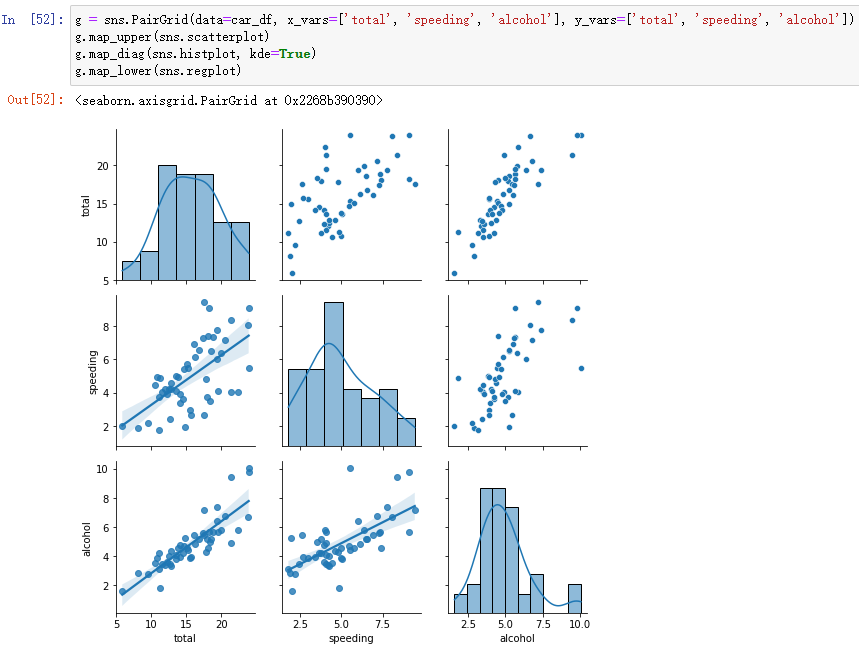
(5)data.corr()+sns.heatmap():成对绘制所有数值变量的相关系数
首先求出每对变量的相关系数 :
car_cor = car_df.corr()
car_cor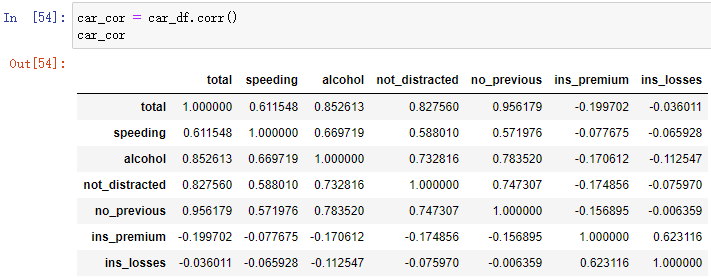 然后用热力图的方式把求到的相关系数表示出来:
然后用热力图的方式把求到的相关系数表示出来:
sns.heatmap(car_cor, cmap='Blues', annot=True, fmt='.2f', linewidth=0.5)
其中annot用来显示数值,fmt='.2f'表示浮点型,保留到小数点后两位。
三、类别变量的分析
1、类别变量的分布:sns.countplot(),类似sns.histplot()
sns.catplot(data=tip_df, x='time', kind='count')
2、类别变量与数值变量的关系
(1)不同类别中数值变量的均值/中值估计:barplot, pointplot
sns.catplot(data=penguin_df, x='species', y='bill_length_mm', kind='bar', estimator=np.median, hue='island')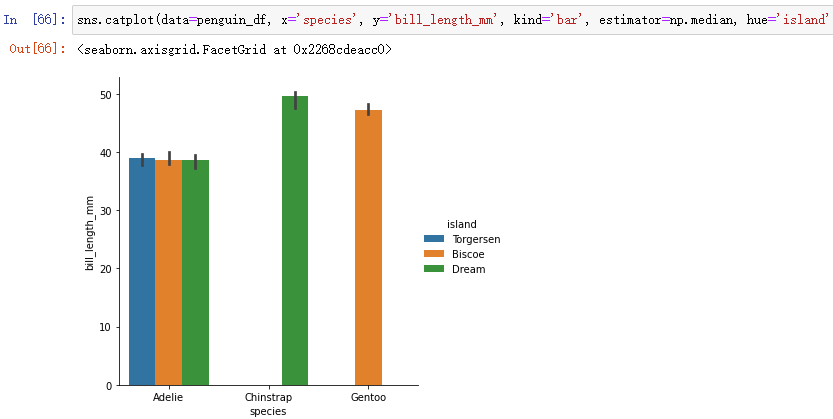
sns.catplot(data=penguin_df, x='species', y='bill_length_mm', kind='point') 
(2)不同类别中数值变量的取值范围:boxplot, boxenplot
sns.catplot(data=penguin_df, x='species', y='bill_length_mm', kind='box') 
一般情况下boxplot就够用了,当变量取值范围很大时,可以用boxenplot(适合大数据集)。boxenplot可以逐级地绘制箱型图。
(3)不同类别中数值变量的分布图:stripplot, swarmplot, violinplot
带状图结合了散点图和直方图的特点:
sns.catplot(data=penguin_df, x='species', y='bill_length_mm', kind='strip',jitter=0.3)通过jitter可以设置带状图的宽度,取值范围[0,1]
swarmplot:
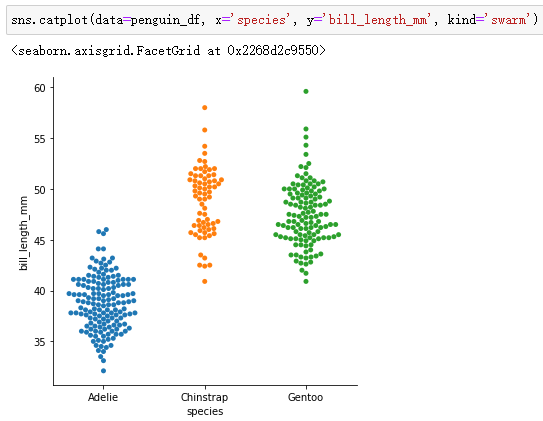
violinplot:
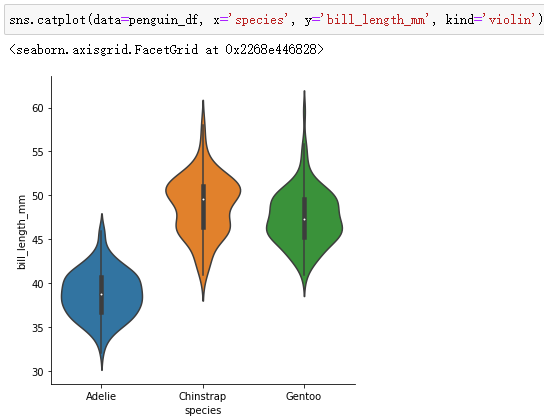
可以将swarmplot 叠加到violinplot上:
sns.catplot(data=penguin_df, x='species', y='bill_length_mm', kind='violin')
sns.swarmplot(data=penguin_df, x='species', y='bill_length_mm', color='w') # 这里要用axes-level
四、FacetGrid, PairGrid中自定义绘制函数
1、FacetGrid
g = sns.FacetGrid(data=tip_df, row='time', col='smoker') # 定义的行列需要是类别变;出来的图只有框线
# 自定义部分
g.map(sns.kdeplot, 'tip')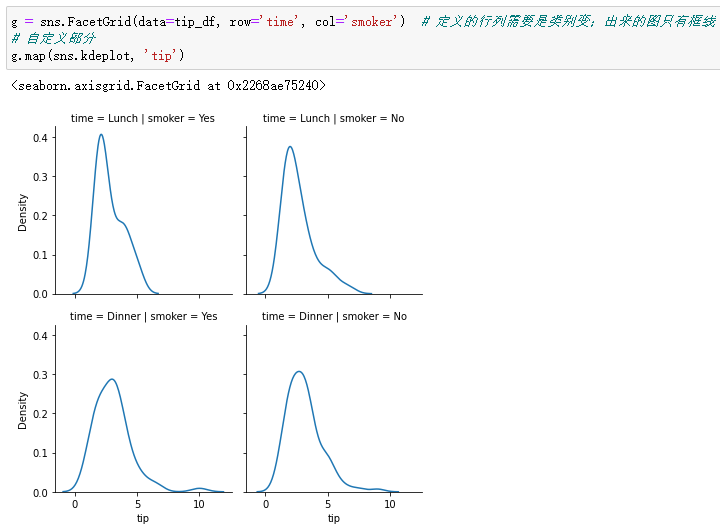
绘制联合分布
g = sns.FacetGrid(data=tip_df, row='time', col='smoker')
# 也可以绘制两个变量的联合分布
g.map(sns.scatterplot,'total_bill', 'tip')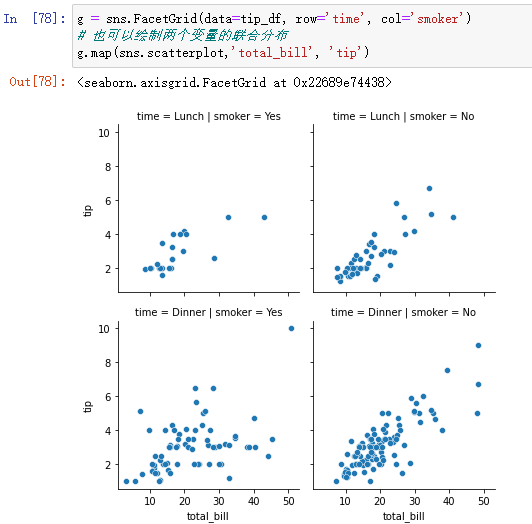
2、PairGrid
用法与pairplot类似
g = sns.PairGrid(data=penguin_df,hue='species')
g.map_diag(sns.kdeplot)
g.map_offdiag(sns.scatterplot)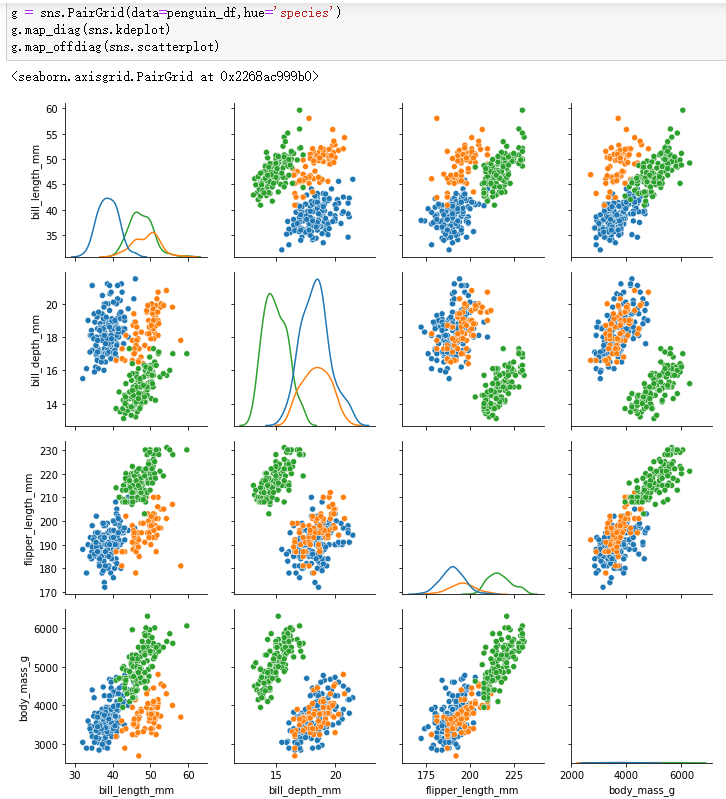
边栏推荐
- NR modulation 1
- Map sorts according to the key value (ascending plus descending)
- 八道超经典指针面试题(三千字详解)
- 深度解析指针与数组笔试题
- My C language learning records (blue bridge) -- files and file input and output
- How to do function test well
- 教你用Pytorch搭建一个自己的简单的BP神经网络( 以iris数据集为例 )
- Selenium share
- Modeling specifications: naming conventions
- Tidb ecological tools (backup, migration, import / export) collation
猜你喜欢

StrError & PERROR use yyds dry inventory
Game theory matlab
Computer graduation project asp Net fitness management system VS development SQLSERVER database web structure c programming computer web page source code project
【指针训练——八道题】

js 正则过滤和增加富文本中图片前缀
IPv6 comprehensive experiment
MPLS experiment

Research on cooperative control of industrial robots

canvas切积木小游戏代码
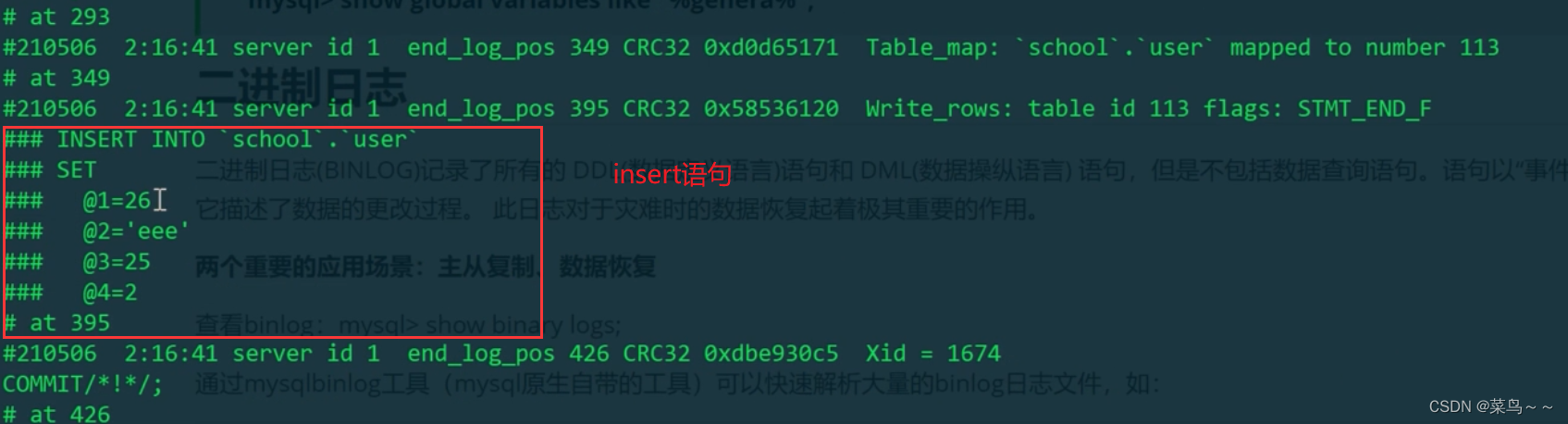
MySQL Server层四个日志
随机推荐
EDCircles: A real-time circle detector with a false detection control 翻译
js凡客banner轮播图js特效
IPv6 comprehensive experiment
Linear programming matlab
Software design principles
Quartz misfire missed and compensated execution
Codeforces 5 questions par jour (1700 chacune) - jour 6
Audio audiorecord binder communication mechanism
Lua uses require to load the shared library successfully, but the return is Boolean (always true)
【 kubernets series】 a Literature Study on the Safe exposure Applications of kubernets Service
Microsoft Research, UIUC & Google research | antagonistic training actor critic based on offline training reinforcement learning
【SLAM】lidar-camera外参标定(港大MarsLab)无需二维码标定板
深入刨析的指针(题解)
【RISC-V】外部中断
[unity3d] GUI control
mysqldump数据备份
Game theory matlab
Arabellacpc 2019 (supplementary question)
The real machine cannot access the shooting range of the virtual machine, and the real machine cannot Ping the virtual machine
Erreur de la carte SD "erreur - 110 whilst initialisation de la carte SD