当前位置:网站首页>Machine learning -- linear regression (sklearn)
Machine learning -- linear regression (sklearn)
2022-07-06 11:53:00 【Want to be a kite】
machine learning – linear regression model (sklearn)
linear regression model Yes : In general form Univariate linear regression and Multiple linear regression , Use L2 Norm Ridge return (Ridge), Use L1 Norm Lasso return (Lasso), Use L1 and L2 Norm ElasticNet Return to ( It's right Lasso Fusion of regression and ridge regression ), Logical regression .
Linear regression -sklearn Library call mode and parameter interpretation :
from sklearn.linear_model import LinearRegression
LinearRegression(fit_intercept=True,normalize=False,copy_X=True,n_jobs=1)
Parameter meaning :
- fit_intercept: Boolean value , Specify whether to calculate the intercept in linear regression , namely b value . If False, Then don't count b value .
- normalize: Boolean value . If False, Then the training samples will be normalized .
- copy_X: Boolean value . If True, Will copy a copy of training data .
- n_jobs: An integer . Specified when tasks are parallel CPU Number . If the value is -1 Then use all available CPU.
attribute
- coef_: The weight vector
- intercept_: intercept b value
Method :
- fit(X,y): Training models .
- predict(X): Use the trained model to predict , And return the predicted value .
- score(X,y): Return the score of prediction performance .
The formula is : s c o r e = ( 1 − u / v ) score=(1 - u/v) score=(1−u/v)
among u = ( ( y t r u e − y p r e d ) ∗ ∗ 2 ) . s u m ( ) , v = ( ( y t r u e − y t r u e . m e a n ( ) ) ∗ ∗ 2 ) . s u m ( ) u=((y_true - y_pred) ** 2).sum(),v=((y_true - y_true.mean()) ** 2).sum() u=((ytrue−ypred)∗∗2).sum(),v=((ytrue−ytrue.mean())∗∗2).sum()
score The maximum is 1, But it may be negative ( The prediction effect is too poor ).score The bigger it is , The better the prediction performance .
Join in L2 Regularized linear regression -sklearn Library call mode and parameter interpretation
from sklearn.linear_model import Ridge
Ridge(alpha=1.0, fit_intercept=True, normalize=False,copy_X=True, max_iter=None,
tol=1e-3, solver=“auto”,random_state=None)
Parameter meaning :
alpha: Coefficient of regular term , The larger the value, the larger the proportion of regular terms . The initial value is suggested to be set to 0, In this way, first determine a better study rate , Once the learning rate is determined , to alpha A smaller value , Then according to the accuracy on the verification set , Increase or decrease 10 times .10 Double coarse adjustment , When the appropriate order of magnitude is determined , Then fine adjust in the same order of magnitude .
fit_intercept: Boolean value , Specify whether intercept calculation is required b value .False It doesn't count b value .
normalize: Boolean value . If it is equal to True, The data will be normalized before model training . There are two benefits : (1): Improve the convergence rate of the model , Reduce the time to find the optimal solution . (2) Improve the accuracy of the model .
copy_X: Boolean value . If set to True, Will copy a copy of training data .
max_iter: Integers . The maximum number of iterations is specified . If None, The default value .
tol: threshold . Judge whether the iteration converges or meets the accuracy requirements .
solver: character string . Specify the algorithm to solve the optimization problem .
(1).solver=‘auto’, Automatic selection algorithm based on data set .
(2).solver=‘svd’, Using the method of singular value decomposition to calculate
(3).solver=‘cholesky’, use scipy.linalg.solve Function to solve the optimal solution .
(4).solver=‘sparse_cg’, use scipy.sparse.linalg.cg Function to find the optimal solution .
(5).solver=‘sag’, use Stochastic Average Gradient descent The algorithm solves the optimization problem .random_state: An integer or a RandomState example , Or for None. It's in solver="sag" When using .
(1). If it's an integer , It specifies the seed of the random number generator .
(2). If RandomState example , The random number generator is specified .
(3). If None, Then use the default random number generator .
attribute :
- coef_: The weight vector .
- intercept_: intercept b Value .
- n_iter_: The actual number of iterations .
Method :
- fit(X,y): Training models .
- predict(X): Use the trained model to predict , And return the predicted value .
- score(X,y): Return the score of prediction performance .
The formula is : s c o r e = ( 1 − u / v ) score=(1 - u/v) score=(1−u/v)
among u = ( ( y t r u e − y p r e d ) ∗ ∗ 2 ) . s u m ( ) , v = ( ( y t r u e − y t r u e . m e a n ( ) ) ∗ ∗ 2 ) . s u m ( ) u=((y_true - y_pred) ** 2).sum(),v=((y_true - y_true.mean()) **2).sum() u=((ytrue−ypred)∗∗2).sum(),v=((ytrue−ytrue.mean())∗∗2).sum()
score The maximum is 1, But it may be negative ( The prediction effect is too poor ).score The bigger it is , The better the prediction performance .
Join in L1 Regularized linear regression -sklearn Library call mode and parameter interpretation
from sklearn.linear_model import Lasso
Lasso(alpha=1.0, fit_intercept=True, normalize=False, precompute=False,
copy_X=True, max_iter=1000,
tol=1e-4, warm_start=False, positive=False,random_state=None,
selection=‘cyclic’)
Parameter meaning :
- alpha: Coefficient of regularization term
- fit_intercept: Boolean value , Specify whether intercept calculation is required b value .False It doesn't count b value .
- max_iter: Specify the maximum number of iterations .
- normalize: Boolean value . If it is equal to True, The data will be normalized before model training . There are two benefits : (1): Improve the convergence rate of the model , Reduce the time to find the optimal solution . (2) Improve the accuracy of the model .
- precompute: A Boolean value or a sequence . It decides whether to calculate in advance Gram Matrix to speed up computation .
- tol: threshold . Judge whether the iteration converges or meets the accuracy requirements .
- warm_start: Boolean value . If True, Then use the results of the previous training to continue training . Or start training from scratch .
- positive: Boolean value . If True, Then force the components of the weight vector to be positive .
- selection: character string , It can be "cyclic" or "random". It specifies when each iteration , Choose which of the weight vectors Component to update .
(1)“random”: When it's updated , Randomly select a component of the weight vector to update .
(2)“cyclic”: When it's updated , Select a component of the weight vector from front to back to update - random_state: An integer or a RandomState example , perhaps None.
(1): If it's an integer , It specifies the seed of the random number generator .
(2): If RandomState example , Then it specifies the random number generator .
(3): If None, Then use the default random number generator .
attribute :
- coef_: The weight vector .
- intercept_: intercept b value .
- n_iter_: The actual number of iterations .
Method :
- fit(X,y): Training models .
- predict(X): Using models to make predictions , Return forecast .
- score(X,y): Return the score of prediction performance .
The formula is : s c o r e = ( 1 − u / v ) score=(1 - u/v) score=(1−u/v)
among u = ( ( y t r u e − y p r e d ) ∗ ∗ 2 ) . s u m ( ) , v = ( ( y t r u e − y t r u e . m e a n ( ) ) ∗ ∗ 2 ) . s u m ( ) u=((y_true - y_pred) ** 2).sum(),v=((y_true - y_true.mean()) ** 2).sum() u=((ytrue−ypred)∗∗2).sum(),v=((ytrue−ytrue.mean())∗∗2).sum()
score The maximum is 1, But it may be negative ( The prediction effect is too poor ).score The bigger it is , The better the prediction performance .
ElasticNet Regression is right Lasso Fusion of regression and ridge regression , The regularization term is L1 Norm sum L2 A trade-off of norms .-sklearn Library call mode and parameter interpretation
The regularization term is : a l p h a ∗ l 1 r a t i o ∗ ∣ ∣ w ∣ ∣ 1 + 0.5 ∗ a l p h a ∗ ( 1 − l 1 r a t i o ) ∗ ∣ ∣ w ∣ ∣ 2 2 alpha * l1_ratio * ||w||_1 + 0.5 * alpha * (1 - l1_ratio) * ||w||^2_2 alpha∗l1ratio∗∣∣w∣∣1+0.5∗alpha∗(1−l1ratio)∗∣∣w∣∣22
from sklearn.linear_model import ElasticNet
ElasticNet(alpha=1.0, l1_ratio=0.5, fit_intercept=True,
normalize=False,precompute=False, max_iter=1000,copy_X=True, tol=1e-4,
warm_start=False, positive=False,random_state=None, selection=‘cyclic’)
Parameter meaning :
- alpha: Regularization term alpha value .
- l1_ratio: In the regularization term l1_ratio value .
- fit_intercept: Boolean value , Specify whether intercept calculation is required b value .False It doesn't count b value .
- max_iter: Specify the maximum number of iterations .
- normalize: Boolean value . If it is equal to True, The data will be normalized before model training . There are two benefits :
(1): Improve the convergence rate of the model , Reduce the time to find the optimal solution .
(2) Improve the accuracy of the model . - copy_X: Boolean value . If set to True, Will copy a copy of training data .
- precompute: A Boolean value or a sequence . It decides whether to calculate in advance Gram Matrix to speed up computation .
- tol: threshold . Judge whether the iteration converges or meets the accuracy requirements .
- warm_start: Boolean value . If True, Then use the results of the previous training to continue training . Or start training from scratch .
- positive: Boolean value . If True, Then force the components of the weight vector to be positive .
- selection: character string , It can be "cyclic" or "random". It specifies when each iteration , Choose which of the weight vectors Components to update .
(1)“random”: When it's updated , Randomly select a component of the weight vector to update .
(2)“cyclic”: When it's updated , Select a component of the weight vector from front to back to update . - random_state: An integer or a RandomState example , perhaps None.
(1): If it's an integer , It specifies the seed of the random number generator .
(2): If RandomState example , Then it specifies the random number generator .
(3): If None, Then use the default random number generator .
attribute :
- coef_: The weight vector .
- intercept_: intercept b value .
- 3.n_iter_: The actual number of iterations .
Method :
- fit(X,y): Training models .
- predict(X): Using models to make predictions , Return forecast .
- score(X,y): Return the score of prediction performance .
The formula is : s c o r e = ( 1 − u / v ) score=(1 - u/v) score=(1−u/v)
among u = ( ( y t r u e − y p r e d ) ∗ ∗ 2 ) . s u m ( ) , v = ( ( y t r u e − y t r u e . m e a n ( ) ) ∗ ∗ 2 ) . s u m ( ) u=((y_true - y_pred) ** 2).sum(),v=((y_true - y_true.mean()) ** 2).sum() u=((ytrue−ypred)∗∗2).sum(),v=((ytrue−ytrue.mean())∗∗2).sum()
score The maximum is 1, But it may be negative ( The prediction effect is too poor ).score The bigger it is , The better the prediction performance .
Logical regression -sklearn Library call mode and parameter interpretation
from sklearn.linear_model import LogisticRegression
LogisticRegression(penalty=‘l2’,dual=False,tol=1e-4,C=1.0,
fit_intercept=True,intercept_scaling=1,class_weight=None,
random_state=None,solver=‘liblinear’,max_iter=100,
multi_class=‘ovr’,verbose=0,warm_start=False,n_jobs=1)
Parameter meaning :
- penalty: character string , The regularization strategy is specified . The default is "l2"
(1) If "l2", Then the objective function of optimization is : 0.5 ∗ ∣ ∣ w ∣ ∣ 2 2 + C ∗ L ( w ) , C > 0 0.5*||w||^2_2+C*L(w),C>0 0.5∗∣∣w∣∣22+C∗L(w),C>0, L(w) Is the maximum likelihood function .
(2) If "l1", Then the objective function of optimization is ∣ ∣ w ∣ ∣ 1 + C ∗ L ( w ) , C > 0 ||w||_1+C*L(w),C>0 ∣∣w∣∣1+C∗L(w),C>0, L(w) Is the maximum likelihood function . - dual: Boolean value . The default is False. If it is equal to True, Then solve its dual form .
Only in penalty="l2" also solver="liblinear" Only when there is a dual form . If False, Then solve the original form . When n_samples > n_features, In favor of dual=False. - tol: threshold . Judge whether the iteration converges or meets the accuracy requirements .
- C:float, The default is 1.0. Specifies the reciprocal of the coefficient of the regularization term . Must be a positive floating point number .C The smaller the value. , The larger the regularization term .
- fit_intercept:bool value . The default is True. If False, You won't calculate b value .
- intercept_scaling:float, default 1. Only when solver="liblinear" also fit_intercept=True when , It makes sense . under these circumstances , It is equivalent to adding a feature in the last column of training data , The characteristic is constant 1. Its corresponding weight is b.
- class_weight:dict or ‘balanced’, default: None.
(1) If it's a dictionary , Then give the weight of each classification . according to {class_label: weight} This form .
(2) If it is "balanced": Then the weight of each classification is inversely proportional to the frequency of the classification in the sample set .
n s a m p l e s / ( n c l a s s e s ∗ n p . b i n c o u n t ( y ) ) n_samples / (n_classes * np.bincount(y)) nsamples/(nclasses∗np.bincount(y))
(3) If not specified , Then the weight of each classification is 1. - random_state: int, RandomState instance or None, default: None
(1): If it's an integer , It specifies the seed of the random number generator .
(2): If RandomState example , Then it specifies the random number generator .
(3): If None, Then use the default random number generator . - solver: character string , Specify the algorithm to solve the optimization problem .
{‘newton-cg’, ‘lbfgs’, ‘liblinear’, ‘sag’, ‘saga’},default: ‘liblinear’
(1)solver=‘liblinear’, For small data sets ,'liblinear’ It's a good choice . For large data sets ,‘sag’ and ’saga’ Faster processing .
(2)solver=‘newton-cg’, Adopt Newton method
(3)solver=‘lbfgs’, use L-BFGS Quasi Newton method .
(4)solver=‘sag’, use Stochastic Average Gradient descent Algorithm .
(5) For multi classification problems , Only ’newton-cg’,‘sag’,'saga’ and ’lbfgs’ Dealing with multiple losses ;
‘liblinear’ Is limited to ’ovr’ programme .
(6)newton-cg’, ‘lbfgs’ and ‘sag’ Can only handle L2 penalty,‘liblinear’ and ‘saga’ Can deal with L1 penalty. - max_iter: Specify the maximum number of iterations .default: 100. Only right ’newton-cg’, ‘sag’ and 'lbfgs’ apply .
- multi_class:{‘ovr’, ‘multinomial’}, default: ‘ovr’. Specify the strategy for classification problems .
(1)multi_class=‘ovr’, use ’one_vs_rest’ Strategy .
(2)multi_class=‘multinomal’, Adopt multiple classification logistic regression strategy directly . - verbose: It is used to turn on or off the iteration intermediate output log function .
- warm_start: Boolean value . If True, Then use the results of the previous training to continue training . Or start training from scratch .
- n_jobs: int, default: 1. When specifying tasks in parallel CPU Number . If -1, Then use all available CPU.
attribute :
- coef_: The weight vector .
- intercept_: intercept b value .
- n_iter_: The actual number of iterations .
Method :
- fit(X,y): Training models .
- predict(X): Use the trained model to predict , And return the predicted value .
- predict_log_proba(X): Returns an array , The array elements, in turn, are X The logarithm of the probability predicted for each category .
- predict_proba(X): Returns an array , The array elements, in turn, are X Prediction is the probability value of each category .
- score(X,y): Returns the accuracy of the forecast .
Practical cases :
Multiple linear regression
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from sklearn import datasets,linear_model,model_selection
from sklearn.model_selection import train_test_split
def load_data():
diabetes = datasets.load_diabetes()
return train_test_split(diabetes.data,diabetes.target,test_size=0.2)
def test_LineearRegression(*data):
X_train,X_test,y_train,y_test = data
regr = linear_model.LinearRegression()
regr.fit(X_train,y_train)
print('Coefficients:{},intercept:{}'.format(regr.coef_,regr.intercept_))
print('Residual sum of squares:{}'.format(np.mean(regr.predict(X_test)-y_test)**2))
print('Scores:{}'.format(regr.score(X_test,y_test)))
if __name__ == '__main__':
X_train,X_test,y_train,y_test = load_data()
test_LineearRegression(X_train,X_test,y_train,y_test)
Lasso Return to
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets,linear_model
from sklearn.model_selection import train_test_split
def load_data():
diabetes = datasets.load_diabetes()
return train_test_split(diabetes.data,diabetes.target,test_size=0.2)
def test_Lasso(*data):
X_train,X_test,y_train,y_test = data
regr = linear_model.Lasso()
regr.fit(X_train,y_train)
print('Coefficients:{},intercept:{}'.format(regr.coef_,regr.intercept_))
print('Residual sum of squares:{}'.format(np.mean(regr.predict(X_test)-y_test)**2))
print('Scores:{}'.format(regr.score(X_test,y_test)))
def test_Lasso_alpha(*data):
X_train,X_test,y_train,y_test = data
alphas = [0.01,0.02,0.05,0.1,0.2,0.5,1,2,5,10,20,50,100,200,500,1000]
scores = []
for i,alpha in enumerate(alphas):
regr = linear_model.Lasso(alpha=alpha)
regr.fit(X_train,y_train)
scores.append(regr.score(X_test,y_test))
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
ax.plot(alphas,scores)
ax.set_xlabel("alpha")
ax.set_ylabel("score")
ax.set_xscale("log")
ax.set_title('Lasso')
plt.show()
if __name__ == '__main__':
X_train,X_test,y_train,y_test = load_data()
test_Lasso(X_train,X_test,y_train,y_test)
test_Lasso_alpha(X_train,X_test,y_train,y_test)
Ridge return (Ridge)
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets,linear_model
from sklearn.model_selection import train_test_split
def load_data():
diabetes = datasets.load_diabetes()
return train_test_split(diabetes.data,diabetes.target,test_size=0.2,random_state=0)
def test_Ridge(*data):
X_train,X_test,y_train,y_test = data
regr = linear_model.Ridge()
regr.fit(X_train,y_train)
print('Coefficients:{},intercept:{}'.format(regr.coef_,regr.intercept_))
print('Residual sum of squares:{}'.format(np.mean(regr.predict(X_test)-y_test)**2))
print('Scores:{}'.format(regr.score(X_test,y_test)))
def test_Ridge_alpha(*data):
X_train,X_test,y_train,y_test = data
alphas = [0.01,0.02,0.05,0.1,0.2,0.5,1,2,5,10,20,50,100,200,500,1000]
scores = []
for i,alpha in enumerate(alphas):
regr = linear_model.Lasso(alpha=alpha)
regr.fit(X_train,y_train)
scores.append(regr.score(X_test,y_test))
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
ax.plot(alphas,scores)
ax.set_xlabel("alpha")
ax.set_ylabel("score")
ax.set_xscale("log")
ax.set_title('Ridge')
plt.show()
if __name__ == '__main__':
X_train,X_test,y_train,y_test = load_data()
test_Ridge(X_train,X_test,y_train,y_test)
test_Ridge_alpha(X_train,X_test,y_train,y_test)
Logical regression
from math import exp
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
def create_data():
iris = load_iris()
df = pd.DataFrame(iris.data,columns=iris.feature_names)
df['label'] = iris.target
df.columns =['sepal length', 'sepal width', 'petal length', 'petal width', 'label']
data = np.array(df.iloc[:100,[0,1,-1]])
return data[:,:2],data[:,-1]
X,y = create_data()
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3)
class LogisticRegressionClassifier(): # Custom method
def __init__(self,max_iter=700,learning_rate=0.01):
self.max_iter = max_iter
self.learning_rate = learning_rate
def sigmoid(self,x):
return x / (1+exp(-1))
def data_matrix(self,X):
data_mat = []
for d in X:
data_mat.append([1.0,*d])
return data_mat
def fit(self, X, y):
data_mat = self.data_matrix(X)
self.weights = np.zeros((len(data_mat[0]), 1), dtype=np.float32)
for iter_ in range(self.max_iter):
for i in range(len(X)):
result = self.sigmoid(np.dot(data_mat[i], self.weights))
error = y[i] - result
self.weights += self.learning_rate * error * np.transpose([data_mat[i]])
print('LogisticRegression Model(learning_rate={}, max_iter={})'.
format(self.learning_rate, self.max_iter))
def score(self, X_test, y_test):
right = 0
X_test = self.data_matrix(X_test)
for x, y in zip(X_test, y_test):
result = np.dot(x, self.weights)
if (result > 0 and y == 1) or (result < 0 and y == 0):
right += 1
return right / len(X_test)
lr_clf = LogisticRegressionClassifier()
lr_clf.fit(X_train, y_train)
lr_clf.score(X_test, y_test)
x_points = np.arange(4, 8)
y_ = -(lr_clf.weights[1] * x_points + lr_clf.weights[0]) / lr_clf.weights[2]
plt.plot(x_points, y_)
plt.scatter(X[:50, 0], X[:50, 1], label='0')
plt.scatter(X[50:, 0], X[50:, 1], label='1')
plt.legend()
# Call mode
Logitic_model = linear_model.LogisticRegression()
Logitic_model.fit(X_train,y_train)
Logitic_model.score(X_test,y_test)
边栏推荐
- Implementation scheme of distributed transaction
- Détails du Protocole Internet
- 小L的试卷
- Wangeditor rich text reference and table usage
- Learn winpwn (2) -- GS protection from scratch
- Vs2019 use wizard to generate an MFC Application
- Valentine's Day flirting with girls to force a small way, one can learn
- [Bluebridge cup 2021 preliminary] weight weighing
- Software I2C based on Hal Library
- 【yarn】CDP集群 Yarn配置capacity调度器批量分配
猜你喜欢
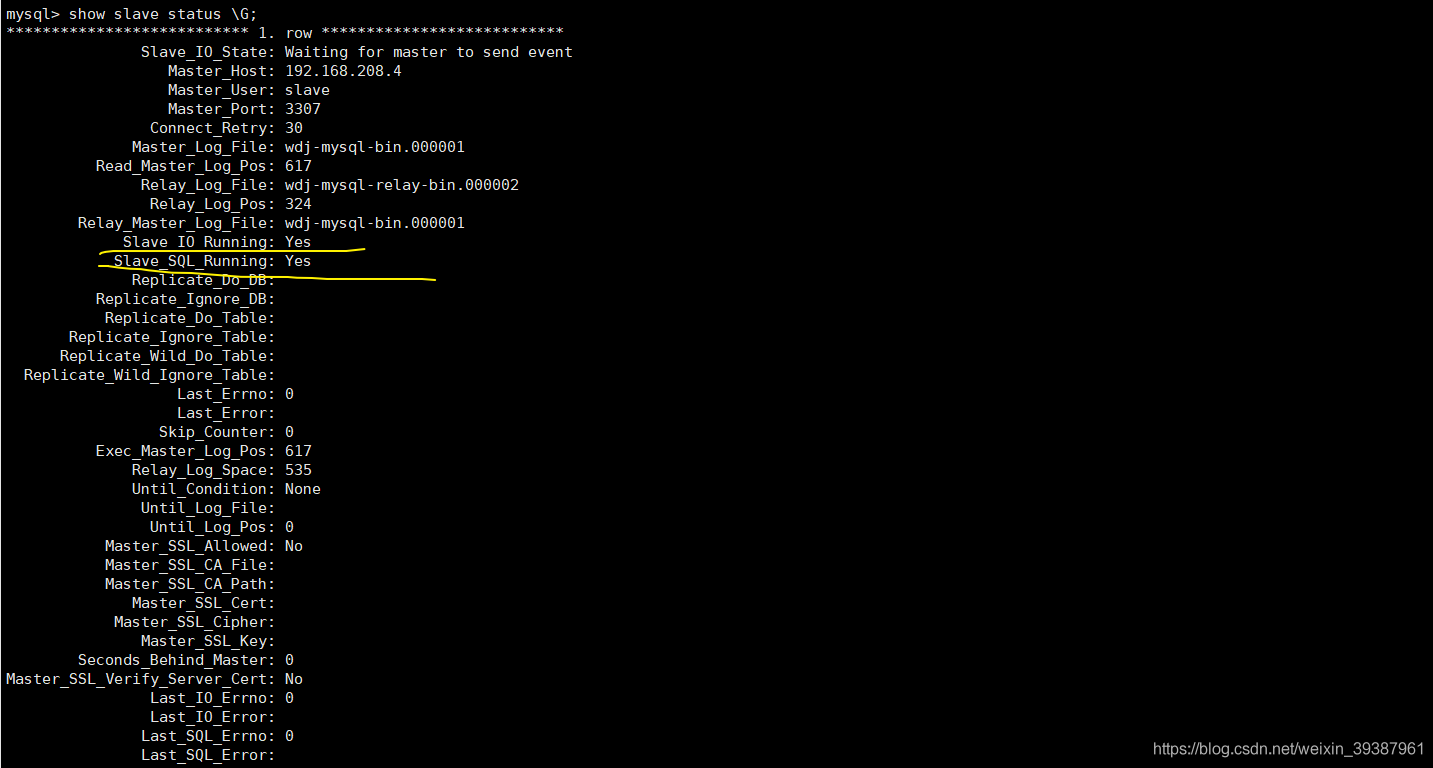
Principle and implementation of MySQL master-slave replication
Reading BMP file with C language
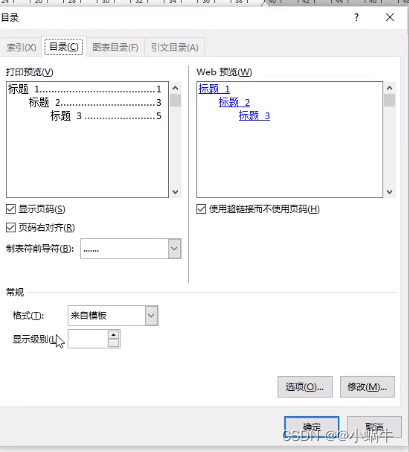
Word typesetting (subtotal)
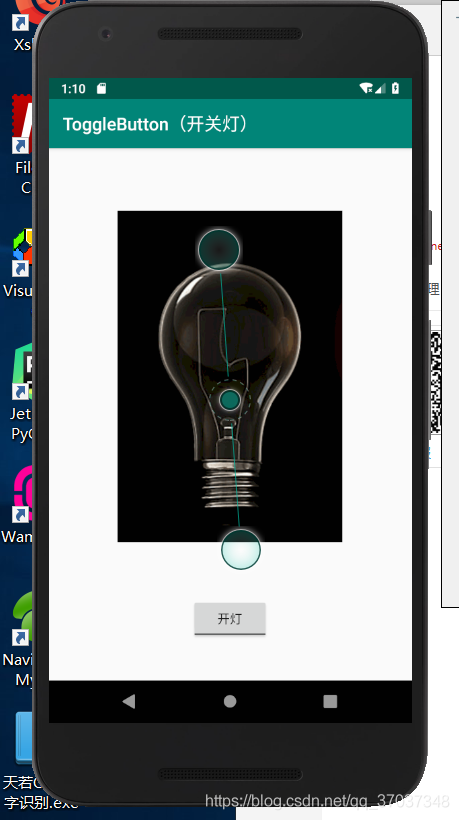
ToggleButton实现一个开关灯的效果
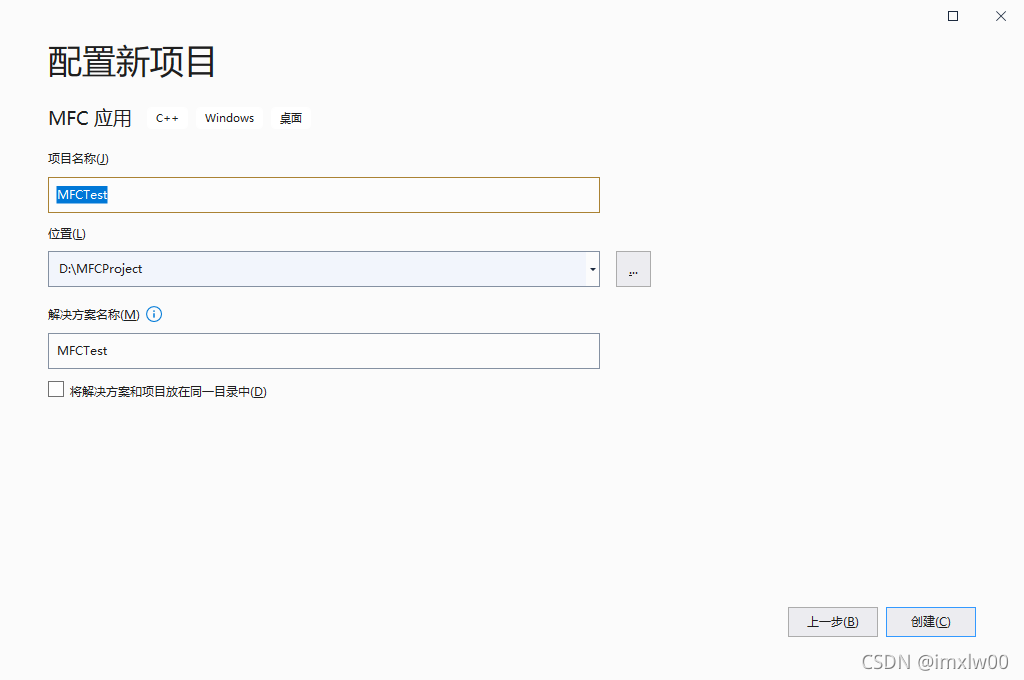
Vs2019 use wizard to generate an MFC Application
Integration test practice (1) theoretical basis
C语言读取BMP文件
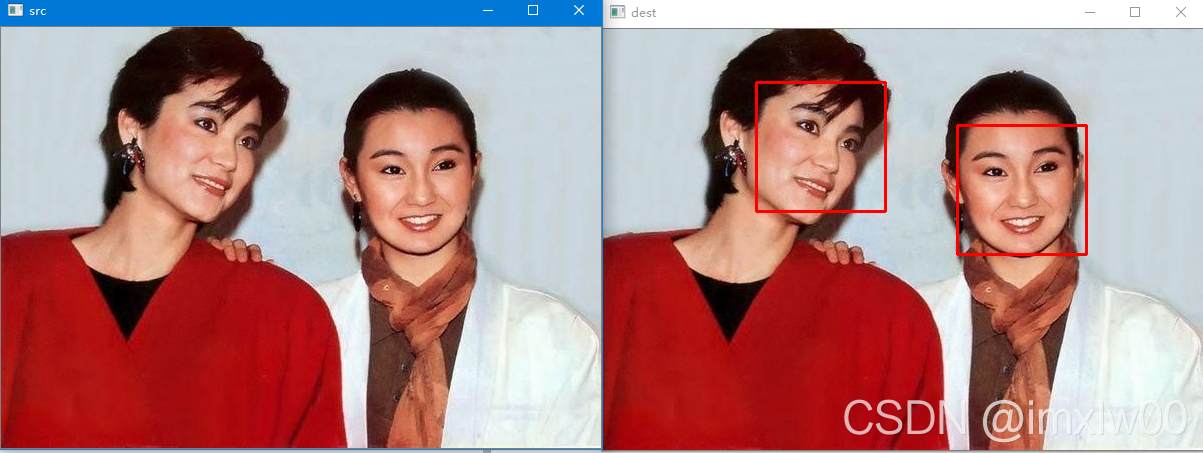
Face recognition_ recognition
wangeditor富文本引用、表格使用问题
Machine learning notes week02 convolutional neural network
随机推荐
小L的试卷
Funny cartoon: Programmer's logic
Using LinkedHashMap to realize the caching of an LRU algorithm
[Presto] Presto parameter configuration optimization
XML file explanation: what is XML, XML configuration file, XML data file, XML file parsing tutorial
[蓝桥杯2020初赛] 平面切分
Nodejs connect mysql
Gallery之图片浏览、组件学习
Redis面试题
Wangeditor rich text component - copy available
TypeScript
MongoDB
ToggleButton实现一个开关灯的效果
2019腾讯暑期实习生正式笔试
分布式节点免密登录
4. Install and deploy spark (spark on Yan mode)
Codeforces Round #753 (Div. 3)
Mtcnn face detection
Linux Yum install MySQL
Codeforces Round #753 (Div. 3)