当前位置:网站首页>关于SIoU《SIoU Loss: More Powerful Learning for Bounding Box Regression Zhora Gevorgyan 》的一些看法及代码实现
关于SIoU《SIoU Loss: More Powerful Learning for Bounding Box Regression Zhora Gevorgyan 》的一些看法及代码实现
2022-07-07 09:06:00 【optimistic丶中】
最近很多公众号都在推这篇文章,但是我在阅读的过程中产生了一些问题,由于代码未开源,理解可能不正确,因此先记录一下,等开源之后对照代码再更深地去理解,也希望如果有大佬看见这篇文章的时候,能对我不成熟的看法给予一些意见。
文章实验的最终损失函数计算如下: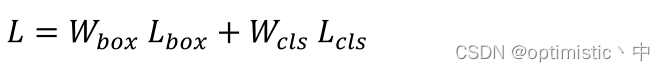
其中 L c l s L_{cls} Lcls是用了focal loss, W b o x W_{box} Wbox和 W c l s W_{cls} Wcls权重参数是根据遗传算法计算得来的, L b o x L_{box} Lbox是本文所提的SIoU损失,计算如下: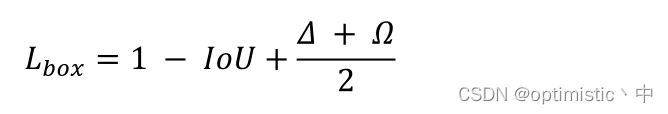
主要是涉及到四部分损失:角度损失 、距离损失 、形状损失 、IoU 损失
1.角度损失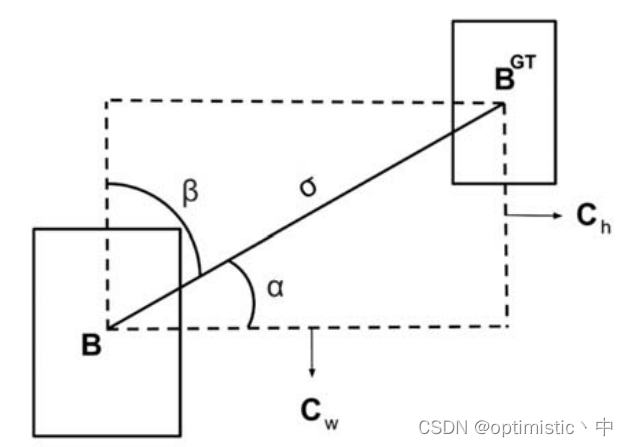
这里作者认为,可以考虑角度因素,首先使得预测框回归到与真值框同一水平线或者垂直线上,这点我很认同,可以加速收敛,作者是通过以下公式评估损失的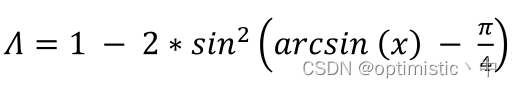
该公式由两部分组成,第一部分是 1 − 2 s i n 2 ( x ) 1-2sin^2(x) 1−2sin2(x),其实也就是 c o s ( 2 x ) cos(2x) cos(2x),使得对于 x > 0 x>0 x>0的情况,其值只有在 x x x为 π / 4 π/4 π/4的时候取最小,得到0,而在 x x x为0的时候取最大,得到1;第二部分是 a r c s i n ( x ) − π / 4 arcsin(x)-π/4 arcsin(x)−π/4,其中 a r c s i n ( x ) arcsin(x) arcsin(x)也就是 α α α,还需要进行 − π / 4 -π/4 −π/4的操作是需要考虑到让预测框朝角度较小的一边进行移动,因为 β β β等于 π / 2 − α π/2-α π/2−α,两者 − π / 4 -π/4 −π/4后互为相反数,经过 c o s cos cos函数计算后的值是一样的,当 α α α为0的时候,其损失最小,而为 π / 4 π/4 π/4的时候最大。最终使得预测框更快地移动到真值框所在的水平线或者垂直线上。
2.距离损失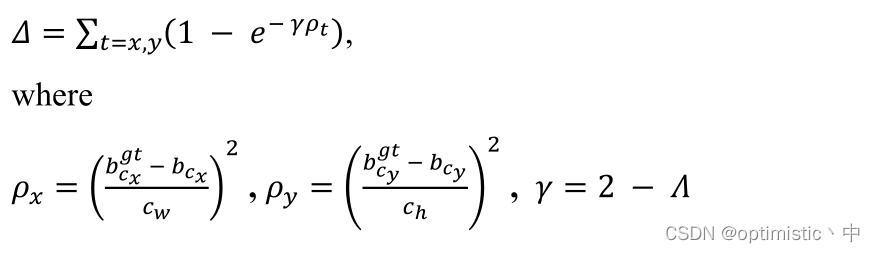
(1)对于 ρ x ρ_x ρx和 ρ y ρ_y ρy的计算,本来还在想这不是一直会计算恒等于1吗,然后发现论文中图3给了图示,这里的 c w c_w cw和 c h c_h ch是指最小外接框的长度。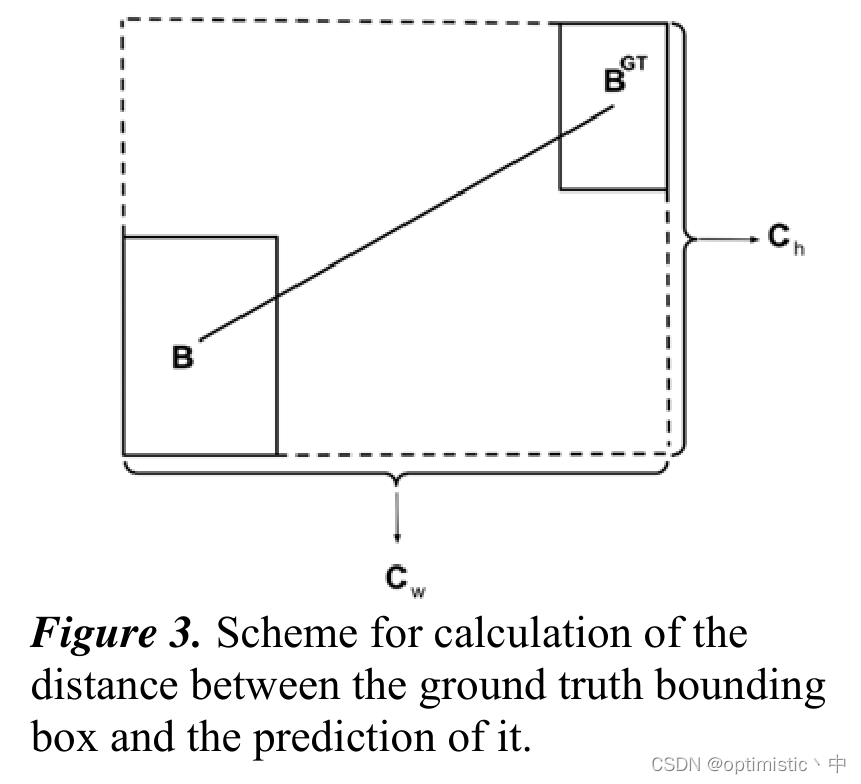
(2)对于 γ γ γ的计算方式,我的理解是首先由角度损失计算可以得到 Λ Λ Λ的范围应该是[0,1],这里再经过 2 − Λ 2-Λ 2−Λ,首先防止 γ γ γ为0时 ρ t ρ_t ρt失效的情况,其次使得 Λ Λ Λ越小, ρ t ρ_t ρt变化对于损失的影响就越大。
3.形状损失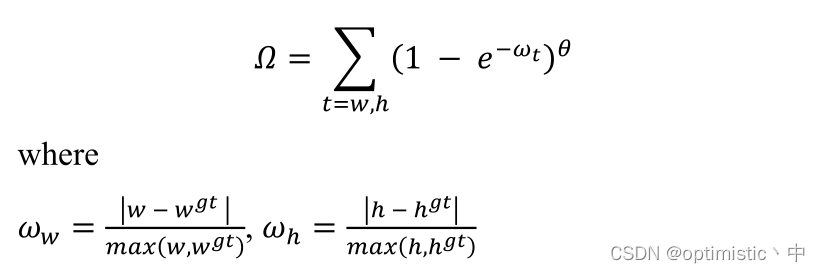
这里和EIOU一样,都考虑到了预测框和真值框之间的真实长宽比,不过对于 ω x ω_x ωx和 ω y ω_y ωy的计算,与EIOU中还需要计算能包围两个框的最小框长宽不一样,这里只用到了真值框和预测框的长宽属性,计算量更少,按理会更快,但是具体效果还不清楚。另外, ω t ω_t ωt的范围是[0,1],我认为应该不需要通过 1 − e − ω t 1-e^{-ω_t} 1−e−ωt进一步计算,说不定效果会更好,最后对于 θ θ θ的引入,这里不是很理解。
(1)首先是不理解为什么引入这个因子会更好。
(2)其次距离损失也是可以引入因子的,为什么不引入。
4.IoU损失
和GIOU里提的一样,这里是按 1 − I o U 1-IoU 1−IoU计算得到
对于文章中的一些权重和 θ θ θ参数都是通过遗传算法对数据集计算得来,不清楚这一部分的提升效果,由于代码未开源,对其中的一些计算方式也存在质疑,因此无法验证每一个改进点真实的效果
以下是我对SIoU的简单复现,如果有误请大佬们勘正
#(x1,y1)和(x2,y2)分别是预测框和真实框的中心坐标
x1 = (b1_x1 + b1_x2) / 2
x2 = (b2_x1 + b2_x2) / 2
y1 = (b1_y1 + b1_y2) / 2
y2 = (b2_y1 + b2_y2) / 2
x_dis = torch.max(x1, x2) - torch.min(x1, x2)
y_dis = torch.max(y1, y2) - torch.min(y1, y2)
sigma = torch.pow(x_dis ** 2 + y_dis ** 2, 0.5) + eps
alpha = y_dis / sigma
beta = x_dis / sigma
threshold = pow(2, 0.5) / 2
sin_alpha = torch.where(alpha > threshold, beta, alpha)
#1 - 2 * sin(x) ** 2 等同于cos(2x)
angle_cost = torch.cos(torch.arcsin(sin_alpha) * 2 - np.pi / 2)
cw += eps
ch += eps
rho_x = (x_dis / cw) ** 2
rho_y = (y_dis / ch) ** 2
gamma = 2 - angle_cost
distance_cost = 2 - torch.exp(-1 * gamma * rho_x) - torch.exp(-1 * gamma * rho_y)
omiga_w = torch.abs(w1 - w2) / (torch.max(w1, w2) + eps)
omiga_h = torch.abs(h1 - h2) / (torch.max(h1, h2) + eps)
# 原论文里提出theta在4附近,范围2到6
theta = 4
shape_cost = torch.pow(1 - torch.exp(-1 * omiga_w), theta) + torch.pow(1 - torch.exp(-1 * omiga_h), theta)
return iou - 0.5 * (distance_cost + shape_cost)
边栏推荐
- [untitled]
- Realize ray detection, drag the mouse to move the object and use the pulley to scale the object
- 一些线上学术报告网站与机器学习视频
- Add a self incrementing sequence number to the antd table component
- "Dream Cup" 2017 Jiangsu information and future primary school summer camp it expert PK program design questions
- Go redis Middleware
- Basic knowledge of process (orphan, zombie process)
- 2021-05-21
- 【OneNote】无法连接到网络,无法同步问题
- Network foundation (1)
猜你喜欢
Online hard core tools
Wallhaven wallpaper desktop version
![[OneNote] can't connect to the network and can't sync the problem](/img/28/9a02b1da0f43889989a9539c9fb6b6.png)
[OneNote] can't connect to the network and can't sync the problem
The concept, implementation and analysis of binary search tree (BST)
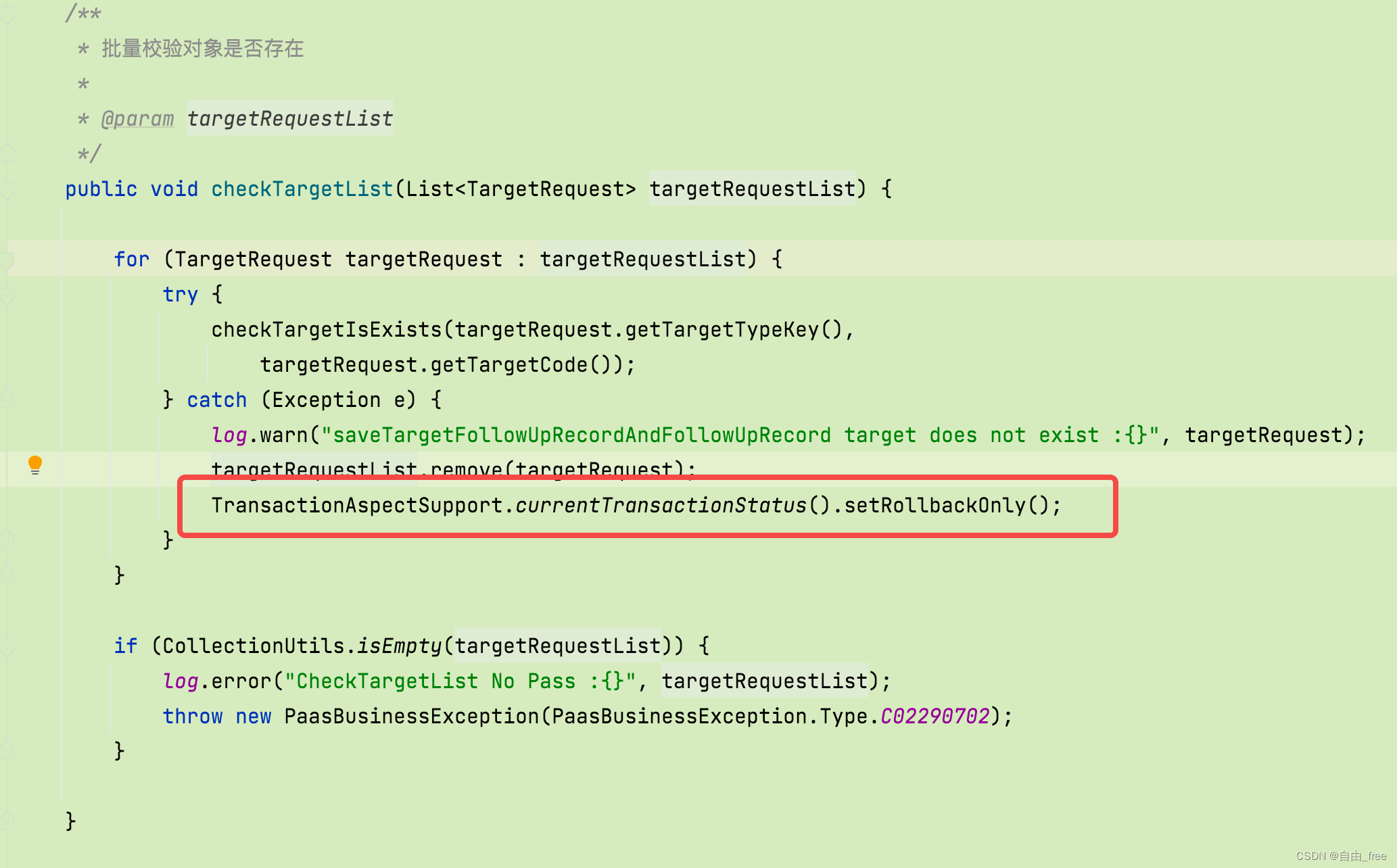
Transaction rolled back because it has been marked as rollback-only解决
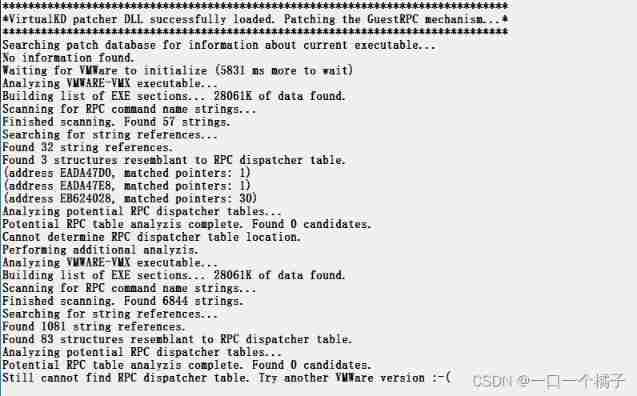
Still cannot find RPC dispatcher table failed to connect in virtual KD

【亲测可行】error while loading shared libraries的解决方案
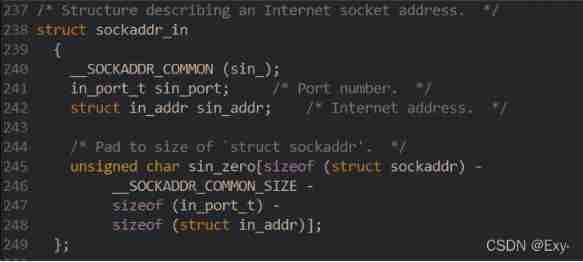
Socket socket programming

JS add spaces to the string
CSAPP bomb lab parsing
随机推荐
從色情直播到直播電商
【OneNote】无法连接到网络,无法同步问题
Galaxy Kirin desktop operating system installation postgresql13 (source code installation)
MPX plug-in
vim 的各种用法,很实用哦,都是本人是在工作中学习和总结的
Shardingsphere sub database and table examples (logical table, real table, binding table, broadcast table, single table)
Get pictures through opencv, change channels and save them
Use load_ decathlon_ Datalist (Monai) fast loading JSON data
Online hard core tools
Network foundation (1)
基于DE2 115开发板驱动HC_SR04超声波测距模块【附源码】
[untitled]
Go Slice 比较
[pyqt] the cellwidget in tablewidget uses signal and slot mechanism
Socket socket programming
"Dream Cup" 2017 Jiangsu information and future primary school summer camp it expert PK program design questions
Opencv installation and environment configuration - vs2017
书签整理-程序员常用网站导航
SQL Server knowledge collection 11: Constraints
[untitled]