【NOI模拟赛】区域划分（结论，构造）

题面

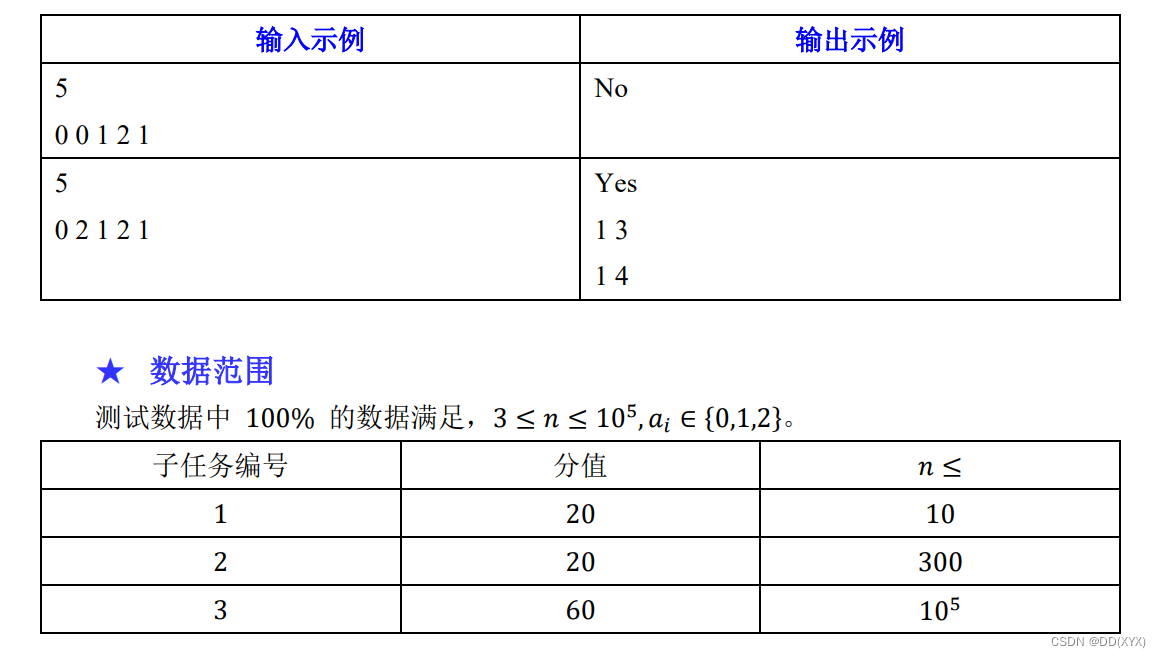
1s , 512mb

题解

首先，如果有相邻两城党派相同一定无解。

我们发现，最终的方案一定得有相邻的三座城市是在一个三角形里的，而把这个三角形连上后，相当于把中间的城市去掉，剩下的部分就又是一个子问题。

于是，我们统计相邻的能组成三角形的三元组个数 $X$（若某位置 $i$ 满足 $a_i$ 和其左右两个位置刚好构成集合 $\{0,1,2\}$ ，则可构成三元组），不难发现，当我们连上一个三角形时，$X$ 减少量为奇数，且存在方案使其大于零。而最终一定是剩三个城，刚好 $X$ 变为 1 的，所以——答案有解当且仅当 $X>0$ 且 $X$ 与 $n$ 的奇偶性相同。

如何使得 $X$ 恒大于零呢？其实只需要尽量使用边缘的三元组——当且仅当某个三元组与左右两个三元组的中心城市相邻时，该三元组不是边缘三元组。若没有边缘的三元组，当然随便选一个连都没问题。因为我们发现，若选了一个非边缘三元组，会使得 $X$ 减少 $3$ ，这时只有全都是非边缘三元组的时候能保证还存在三元组。

于是我们用 set 和链表维护三元组，时间复杂度 $O(n\log n)$ 。

---

看了题解后，我发现我是个XX。

首先，若无相邻相同城市，则 $X$ 的奇偶性一定与 $n$ 相同。也就是说只要 $X>0$ 就有解了。而且不难证明，只要同时存在 $0,1,2$ ，$X$ 就大于 0 。

然后，有很简单的构造法：

CODE

打着我的小笨码，逃避着我的小笨责任

#include<map>
#include<set>
#include<cmath>
#include<ctime>
#include<queue>
#include<stack>
#include<random>
#include<bitset>
#include<vector>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<unordered_map>
#pragma GCC optimize(2)
using namespace std;
#define MAXN 100005
#define LL long long
#define ULL unsigned long long
#define ENDL putchar('\n')
#define DB double
#define lowbit(x) (-(x) & (x))
#define FI first
#define SE second
#define PR pair<int,int>
#define UIN unsigned int
#define eps 1e-6
int xchar() {
    
	static const int maxn = 1000000;
	static char b[maxn];
	static int pos = 0,len = 0;
	if(pos == len) pos = 0,len = fread(b,1,maxn,stdin);
	if(pos == len) return -1;
	return b[pos ++];
}
// #define getchar() xchar()
inline LL read() {
    
	LL f = 1,x = 0;int s = getchar();
	while(s < '0' || s > '9') {
    if(s<0)return -1;if(s=='-')f=-f;s = getchar();}
	while(s >= '0' && s <= '9') {
    x = (x<<1) + (x<<3) + (s^48);s = getchar();}
	return f*x;
}
void putpos(LL x) {
    if(!x)return ;putpos(x/10);putchar((x%10)^48);}
inline void putnum(LL x) {
    
	if(!x) {
    putchar('0');return ;}
	if(x<0) putchar('-'),x = -x;
	return putpos(x);
}
inline void AIput(LL x,int c) {
    putnum(x);putchar(c);}

int n,m,s,o,k;
int a[MAXN];
int l[MAXN],r[MAXN];
set<int> st,sp;
bool che(int x) {
    
	if(a[l[x]]^a[x]^a[r[x]]) return st.erase(x),0;
	return st.insert(x),1;
}
bool che2(int x) {
    
	if(!(a[l[x]]^a[x]^a[r[x]]) && ((a[l[l[x]]]^a[l[x]]^a[x]) || (a[x]^a[r[x]]^a[r[r[x]]]))) return sp.insert(x),1;
	return sp.erase(x),0;
}
void del(int x) {
    
	st.erase(x); sp.erase(x);
	int s = l[x],o = r[x];
	AIput(min(s,o)+1,' '); AIput(max(s,o)+1,'\n');
	r[s] = o; l[o] = s;
	che(s); che(o); che2(s); che2(o);
	che2(l[s]); che2(r[o]);
}
int main() {
    
	freopen("divide.in","r",stdin);
	freopen("divide.out","w",stdout);
	n = read();
	for(int i = 0;i < n;i ++) a[i] = read()+1;
	for(int i = 0;i < n;i ++) {
    
		if(a[i] == a[(i+1)%n]) return printf("No\n"),0;
		l[i] = (i+n-1)%n; r[i] = (i+1)%n;
	}
	for(int i = 0;i < n;i ++) che(i),che2(i);
	if((st.size()&1) == (n&1) && !st.empty()) {
    
		printf("Yes\n");
		for(int i = 1;i <= n-3;i ++) {
    
			int t = *st.begin();
			while(!sp.empty() && !che2(*sp.begin()));
			if(!sp.empty()) t = *sp.begin();
			del(t); while(!st.empty() && !che(*st.begin()));
		}
	}
	else printf("No");
	return 0;
}